标签:部分 bsp target ++ 实现 void 相交 sans 技术
详解并查集
Powered by WSY in SSF
2019-11-02 13:46
【1】并查集的定义:
并查集(Disjoint Set)是一种非常精巧的非常实用的数据结构,它主要用来处理一些不相交集合的合并问题,经典的例子有联通子图,最小生成树的克鲁斯-卡尔算法。
【2】并查集的经典问题:
我们通常使用“帮派”、“团伙”等问题举例说明并查集。例如帮派问题:
在某城市里住着n个人,任何两个认识的人不是朋友就是敌人,而且满足: 1、 我朋友的朋友是我的朋友; 2、 我敌人的敌人是我的朋友; 所有是朋友的人组成一个团伙。告诉你关于这n个人的m条信息,即某两个人是朋友,或者某两个人是敌人,请你编写一个程序,计算出这个城市最多可能有多少个团伙?
这是一个非常经典的并查集问题,接下来就用这个问题的代码为您详解并查集。
【3】并查集问题的基本思路:
第一步 初始化:
我们需要对存储公共祖先的数组进行初始化,一般情况下,将该数组命名为S。
首先,我们说 s[i] 是以节点 i 为元素的独立集合,在开始的时候不处理他和它的朋友之间的关系。
然后,以元素 i 的值表示他的集 s[i] 的值,例如 元素1的集 s[1]=1,如图1.1所示。
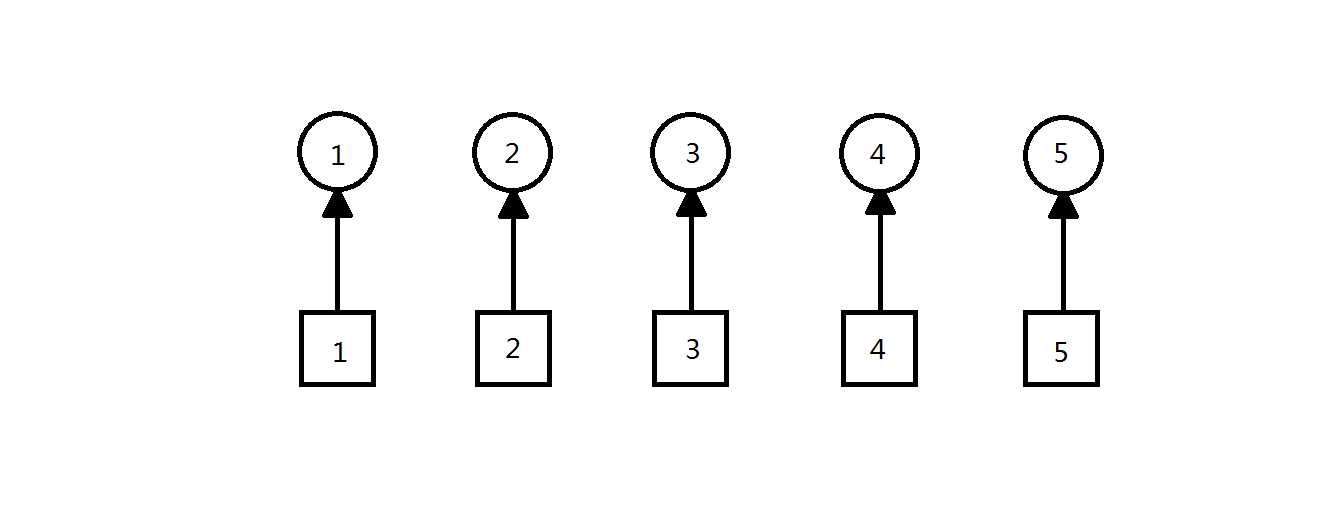
第二步 计算+合并:
合并,例如加入第1个朋友关系(1,2),如图1.2所示,在并查集S中,把节点1合并到节点2。
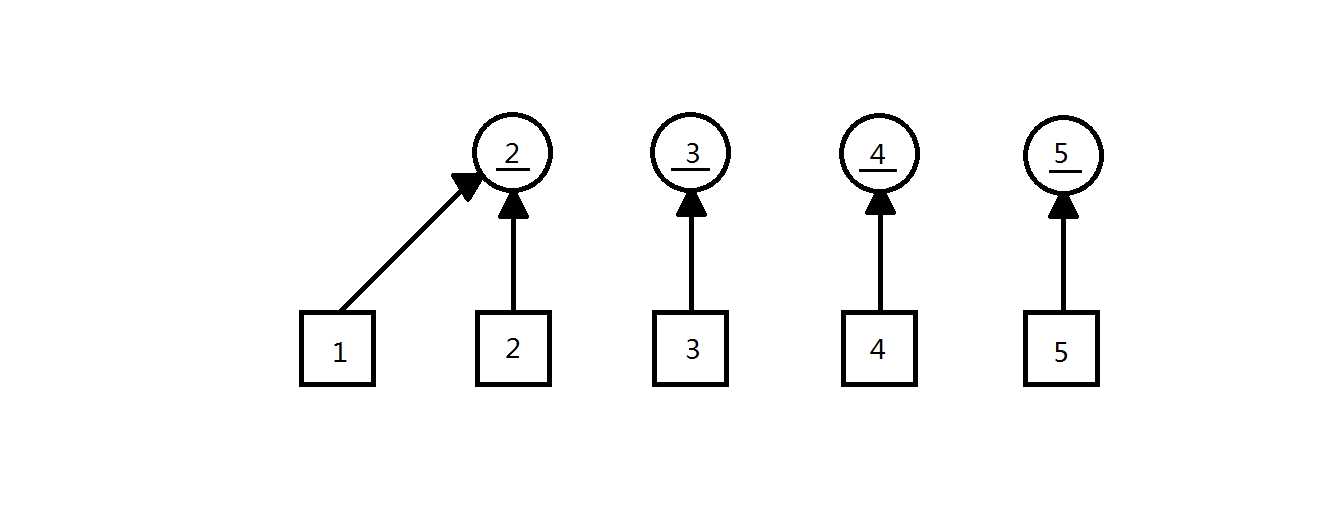
之后,以此类推,直到合并成如图1.3的样子。
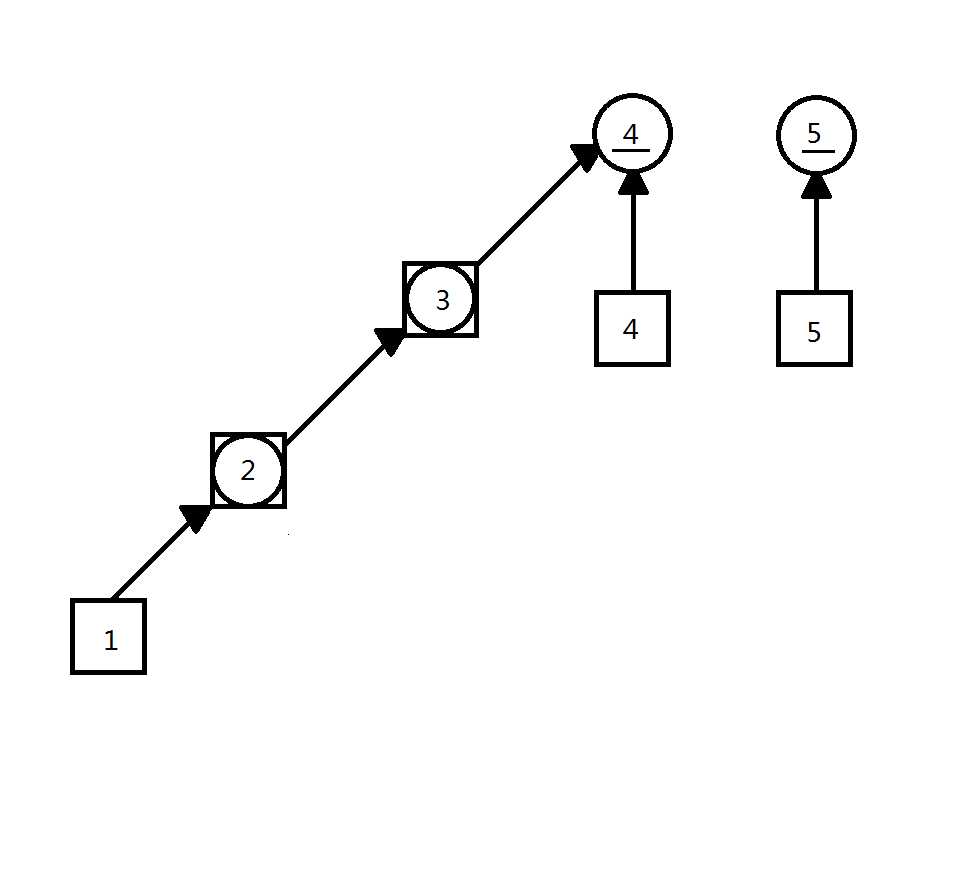
代码君:
1 #include<bits/stdc++.h>
2 using namespace std;
3 const int MAXN=1000+50;
4 int R[MAXN],enemry[MAXN];
5 int Find(int x)
6 {
7 return (!R[x])?x:(Find(R[x]));
8 }
9 void Union(int a, int b)
10 {
11 a=Find(a);
12 b=Find(b);
13 if(a==b) return;
14 if(a!=b) R[b]=a;
15 }
16 int main()
17 {
18 memset(R,0,sizeof(R));
19 memset(enemry,0,sizeof(enemry));
20 int m,n,x,y,j;
21 int ans=0;
22 char ch;
23 cin>>n>>m;
24 for(int i=0;i<m;i++)
25 {
26 cin>>ch>>x>>y;
27 if(ch==‘0‘)
28 {
29 if(enemry[x]) Union(y,enemry[x]);
30 else enemry[x]=y;
31 if(enemry[y]) Union(x,enemry[y]);
32 else enemry[y]=x;
33 }
34 else Union(x,y);
35 }
36 for(int i=1;i<=n;i++)
37 {
38 j=Find(i);
39 if(j==i) ans++;
40 }
41 cout<<ans<<endl;
42 return 0;
43 }//代码来源:https://blog.csdn.net/hyqsblog/article/details/45057877
【4】代码解读+详解
再次感谢 https://blog.csdn.net/hyqsblog/article/details/45057877 提供的代码。
从主函数开始。
第18-19行,第1部分,初始化
初始化R数组,enemry数组(这里很重要,在某些涉及到多组数据的题目时,初始化如果不写,会酿成大错)
第20-23行,第2部分,基础定义+输入
这里定义了一些基本的,后面需要使用的变量。
之后还有一些基础的输入,包括N和M。
第24-35行,第3部分,循环查找,实现并查集中的 “合并”
循环,循环每组关系,查找。
Line 27:如果这组关系是 “敌对”,那么就使用Union函数实现 “敌对合并” 的操作
Line 34:如果这组关系是 “友好”,那么就使用Union函数实现 “友好合并” 的操作
第9-15行,第4部分,实现合并
使用Find函数实现查找合并
第5-8行,第5部分,实现查找
全文只有一句话,但是能实现具体的返回判断,使用二次元运算符
标签:部分 bsp target ++ 实现 void 相交 sans 技术
原文地址:https://www.cnblogs.com/Monach/p/11782835.html