标签：它的   不难   div   树的高度   strong   树的定义   慢慢   理想   自底向上   

１ 引言

RB-Tree，即红黑树，它的定义如下：

1. 这是一颗二叉树，且每个节点要么是红色、要么是黑色
2. 根节点是黑色
3. 叶子节点也是黑色的，且叶子节点不存储数据，即叶子节点是nil空节点
4. 不能出现连续的红色节点，即相邻的红色节点必须被黑色节点隔开
5. 任何一个节点到达其任意一个叶子节点均包含相同数目的黑色节点

单看上面的定义，大家肯定跟我一样一头雾水，别急，下面我们从最简单的二叉查找树说起，慢慢撕开这个高级数据结构的神秘面纱。

2 从二叉查找树到红黑树的演变

2.1 二叉查找树

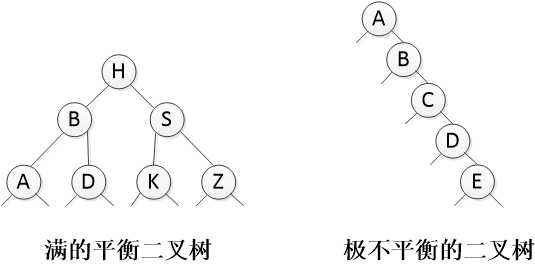
一棵二叉查找树，每个节点的左节点均比当前节点小，且右节点均比当前节点大。上图的两棵树，均属于二叉查找树。于是，查找的过程如下：

• 当前节点等于目标值时，查找成功
• 当查找到空节点时，查找结束，返回不成功
• 小于时，继续在左子树中查找
• 大于时，继续在右子树中查找

最好的情况下，上图左侧示例，当所有节点的左右子树的高度都相同时，无论查找值是什么，每遍历一个节点都能排除一半的可能，这种情况的时间复杂度是O(logN)
最坏的情况下，上图右侧示例，当所有节点都集中在一条路径上，此时二叉查找树已经退化为一个链表，时间复杂度增大到O(N)
随着不断的增删操作，二叉查找树的时间复杂度变得不可控，介于O(logN)和O(N)之间。

有没有可能一直控制在最好的情况下呢，请看下一节：平衡二叉查找树

2.2 平衡二叉查找树

上一节讲到二叉查找树在最坏情况下会退化为链表，如果能保证每个节点的左右子树都是平衡的，即任意节点的左右子树的高度差均不大于1，那么查找的时间复杂度可以稳定在O(logN)。这就是平衡二叉查找树。
平衡二叉查找树的时间复杂度稳定在O(logN)。
但它同时给插入和删除操作带来了麻烦，每次插入或删除后，我们均需要确认这次操作是否影响了整棵树的平衡性，并在全局范围内作出适当调整。这种全局性对编码要求很高，难以实现且不说，额外的维持平衡的逻辑也大大增加了每次插入或删除的消耗，时间复杂度并不比普通二叉查找树优秀。

所以接下来大家不难想到，能否设计一种数据结构能够把全局的平衡性调整简化为局部的调整，从而简化代码实现难度，进而也降低时间复杂度？我们继续看下一节：2-3树

2.3 2-3树

2-3树是由2节点或3节点组成的树结构。这里的2或3指的是每个节点的子树数量：

• 2节点：保存1个key，左子树均小于key，右子树均大于key
• 3节点：保存2个key，左子树均小于最小key，中子树介于两个key之间，右子树均大于key
• 相应的，我们可以得出4节点的定义，即保存3个key，同时划分出4个区间对应于4棵子树

一棵完整的2-3树，高度平衡，即任意节点到达其任意叶子节点的路径长度均相同，也即任意叶子节点的深度是相同的。所以一棵完整的2-3树，就是一棵满的2叉和3叉树，复杂度：

• 最好情况：整棵树均由3节点组成，每遍历一个节点能排除2/3的数据，时间复杂度是 2/3 O(logN)
• 最坏情况：整棵树均由2节点组成，就是一棵满的平衡二叉树，时间复杂度是O(logN)

完整的2-3树的查找时间复杂度：O(logN)

接下来我们以插入操作为例，来看看2-3树是怎么把平衡二叉树要求的全局平衡性调整简化为局部的调整：

对单个节点的插入处理(如上图)

1. 插入S到空节点：直接生成S节点（这一步只可能发生在整棵树为空时。二叉树的插入是在叶子节点后插入一个新节点，树是自顶向下生长的；而2-3树则要求）
2. 插入H到2节点：得到一个3节点(H S)
3. 插入K到3节点：
   3.1 得到一个临时4节点(H K S)
   3.2 临时4节点裂变成3个2节点：将中间key拿出来得到K节点，最小/最大key分别为K节点的左右子节点

注意：第1步只可能发生在整棵树为空时。

• 二叉树是自顶向下生长：插入操作是在叶子节点后新建一个子节点
• 2-3树是自底向上生长：数据插入有值的叶子节点中，随着插入不断进行，底层节点不断往上裂变，直到根节点由4节点裂变成3个2节点时，树高才会+1

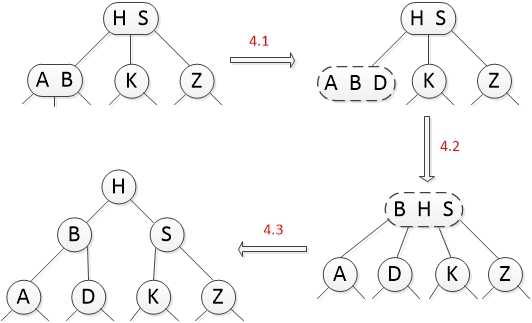
插入操作在一棵树内的处理(如上图)

4.将D节点插入一棵现有的树时，会触发自底向上的递归式调整：
4.1 得到一个临时4节点node1(A B D)
4.2 node1裂变，由于父节点(H S)已存在，所以中间key插入到父节点，又得到一个临时节点node2(B H S)
4.3 node2裂变，由于Node2就是根节点，所以整棵树的高度+1，新的根节点是node2的中间key(H)

上面的1/2/3/4这4个步骤，即是对一棵2-3树的插入操作可能涉及的情况，不难发现，对2-3树的插入可以是一个递归过程，每次只处理单个节点即局部的逻辑，整棵树是自平衡的。递归逻辑如下：

• 根节点为空时，在根节点中插入key
• 根节点非空时：
• 先执行搜索，找到相同的key则替换；
• 未找到key时，将key插入当前节点，即查找的最后一个节点：
  A. 当前节点为2节点，则插入后得到一个3节点，结束递归
  B. 当前节点为3节点，则插入后得到一个4节点，裂变： a. 当前节点为根节点，则裂变后结束递归 b. 否则，将中间key拿出插入到当前节点的父节点，以父节点作为当前节点继续第A步

2-3树的删除操作在此省略。

现在我们知道2-3树在平衡二叉树的基础上进行了优化，保持平衡即查找复杂度O(logN)的同时能够将每次的调整都控制在局部范围内。但2-3树的实现需要处理两种类型的节点，即2节点和3节点，这就增加了代码实现的复杂度，同时这个复杂的代码引起的消耗也不小，所以2-3树的插入或删除时的时间复杂度还不够理想。

所以接下来就是重头戏了，能否用一种节点来实现2-3树，即用二叉树来实现2-3树，将查找、插入、删除、修改的时间复杂度都控制在一个合理的O(logN)？

2.4 红黑树

上一节的2-3树，其中的3节点如果我们用一个红黑的链接来表示，那么一棵2-3树可以转换成这样：

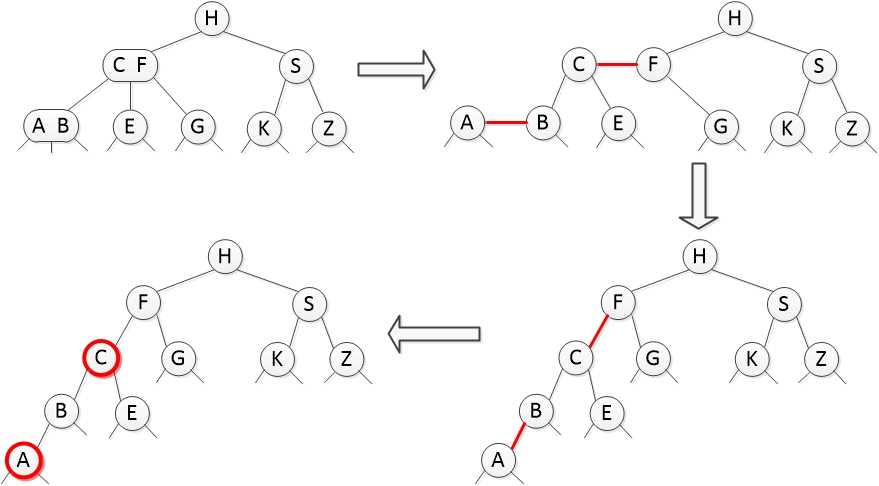
上图中我们对一棵2-3树作了处理，2节点固定为黑色，而3节点可以分解为2个用红色链接连接的2节点，然后将红色链接指向的孩子节点标记为红色，其他节点默认为黑色。事实上这样处理之后，我们就得到了一个红黑树。（注意，上图我们按左倾的方式拆分3节点，同样也可以右倾，即小key作为父节点，大key作为孩子节点）

红黑树既是二叉搜索树，又是特殊的2-3树，现在我们再以2-3树的性质来分析红黑树的定义，就容易理解了：

1. 这是一颗二叉树，且每个节点要么是红色、要么是黑色
2. 根节点是黑色
3. 叶子节点也是黑色的，且叶子节点不存储数据，即叶子节点是nil空节点
4. 不能出现连续的红色节点，即相邻的红色节点必须被黑色节点隔开
5. 任何一个节点到达其任意一个叶子节点均包含相同数目的黑色节点

第1条略过。
第3条是为了后续代码实现的便利性而设定的要求
第2/4条，其实是因为根据上面的转换方式，一个3节点分解成一个黑色的父节点和一个红色的孩子节点，那么红色节点一定会存在一个黑色的父节点。于是根节点没有父节点所以只能是黑色；红色节点的父节点一定是黑色的所以不可能存在相邻的红色节点。
第5条也好理解，正是将红色节点去除，即复原3节点后，能够得到一棵完整的2-3树，树的每个节点的左右子树的高度相等。

红黑树以二叉树的结构实现了一棵特殊的2-3树，由于拆分了3节点，所以树高增加了，那么查找的时间复杂度还有保证吗？

• 最好的情况：所有节点的左右子树的高度一致时，就是一棵满的平衡二叉树，时间复杂度是O(logN)
• 最坏的情况：红黑树最不平衡的状态就是本节开头画的那棵，红色节点全部集中在一条链路上。这时查找只有黑色节点的分支时，需要遍历的节点数小于O(logN)，时间复杂度就是O(logN)。查找红色节点所在的分支时，由于红色节点总是被黑色节点隔开，所以查找路径需要经历的红色节点数最大等于黑色节点数，而根据红黑树定义第5条，从根节点到叶子节点的任意路径的黑色节点固定，同样也小于O(logN)，所以最坏的时间复杂度是小于O(logN)乘以2的。可以认为最坏的时间复杂度近似于O(logN)

所以红黑树的查找时间复杂度稳定在O(logN)。

红黑树一：从二叉树、2-3树到红黑树，一步步讲解红黑树的来源

标签：它的   不难   div   树的高度   strong   树的定义   慢慢   理想   自底向上   

原文地址：https://www.cnblogs.com/JoZSM/p/11784163.html