2019.10.1 qbxt模拟题

标签：ace   两种   span   图片   代码   add   struct   复杂度   第一题   

第一题

考虑树上\(DP\)，f[i][j][0/1]表示以\(i\)为根的子树，入读为零点的个数为\(j\)，点\(i\)的入度为\(0\)/不为\(0\)时的方案数

转移的时候考虑\(u\)的一个子树\(v\)的贡献，分类讨论边\((u,v)\)的两个方向的两个方案，具体的转移方程看代码

记录子树size，利用“刷表法”，只进行有用的转移，复杂度\(O(n^2)\)

#include<iostream>
#include<cstring>
#include<cstdio>
#define LL long long
using namespace std;

const int MAXN=5010;
const int MOD=1000000007;
const int ch_top=4e7+3;
char ch[ch_top],*now_r=ch-1;

inline int read(){
    while(*++now_r<'0');
    register int x=*now_r-'0';
    while(*++now_r>='0') x=x*10+*now_r-'0';
    return x;
}

int n,m;
LL f[MAXN][MAXN][2];

int Head[MAXN],num;
struct NODE{
    int to,nxt;
} e[MAXN<<1];

inline void add(int x,int y){
    e[++num].to=y;
    e[num].nxt=Head[x];
    Head[x]=num;
}

LL g[MAXN][2];
int sz[MAXN];
inline void dfs(int u,int fa){
    sz[u]=f[u][1][0]=1;
    for(int i=Head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        for(int j=0;j<=sz[u]+sz[v];++j) g[j][0]=g[j][1]=0;
        for(int j=0;j<=sz[u];++j)
            for(int k=1;k<=sz[v];++k){
                g[j+k-1][1]+=f[u][j][0]*(f[v][k][0]+f[v][k][1]);
                g[j+k-1][1]+=f[u][j][1]*f[v][k][0];
                g[j+k-1][0]+=f[u][j][0]*f[v][k][0];
                g[j+k][1]+=f[u][j][1]*(f[v][k][1]*2+f[v][k][0]);
                g[j+k][0]+=f[u][j][0]*f[v][k][1];
                g[j+k-1][1]%=MOD; g[j+k-1][0]%=MOD;
                g[j+k][0]%=MOD; g[j+k][1]%=MOD;
            }
        for(int j=0;j<=sz[u]+sz[v];++j)
            f[u][j][0]=g[j][0],f[u][j][1]=g[j][1];
        sz[u]+=sz[v];
    }
}

signed main()
{
    fread(ch,1,ch_top,stdin);
    n=read(); m=read();
    if(m>=n){
        puts("0");
        return 0;
    }
    int x,y;
    for(int i=1;i<n;++i){
        x=read(); y=read();
        add(x,y); add(y,x);
    }
    dfs(1,0);
    printf("%lld\n",(f[1][m][1]+f[1][m][0])%MOD);
    return 0;
}
/*
9 4
1 2
2 9
1 3
3 4
3 5
4 8
5 6
5 7

4 2
1 2
1 3
2 4
*/

第二题

不妨设一个数\(x\)为\(1\)，可以进行两种操作：

\(x=x<<1\)，1的个数不增加，即代价为0

\(x=x<<1|1\)，1的个数+1，即代价为1

当x为n的倍数且代价最小时即为答案，考虑最后的答案是一个\(n\)的倍数，不妨利用这个性质，将所有整数对\(n\)取模，其中为0的数可以作为答案，那么问题就转化为了1->0的最短路

#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;

const int MAXN=1000010;

inline int read(){
    int x=0; char c=getchar();
    while(c<'0') c=getchar();
    while(c>='0') x=(x<<3)+(x<<1)+c-'0',c=getchar();
    return x;
}

int T,n,dis[MAXN];
deque<int> que;

int main()
{
    T=read();
    while(T--){
        n=read();
        memset(dis,0x3f,sizeof(dis));
        dis[1]=1;
        que.clear();
        que.push_back(1);
        while(!que.empty()){
            int u=que.front();
            if(u==0) break;
            que.pop_front();
            int v=u*2%n;
            if(dis[v]>dis[u]){
                dis[v]=dis[u];
                que.push_front(v);
            }
            v=(v+1)%n;
            if(dis[v]>dis[u]+1){
                dis[v]=dis[u]+1;
                que.push_back(v);
            }
        }
        printf("%d\n",dis[0]);
    }
    return 0;
}

第三题

四元环计数模板

类似于三元环计数，考虑将点划分权重，每条边从度数大的点到度数小的点定向，那么一个四元环就会变成这样

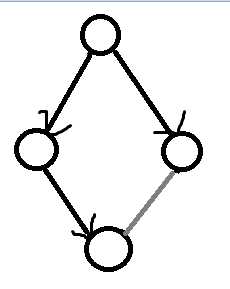
灰边的方向有两种情况，但是每个四元环只能从一个点开始遍历找到

爆搜两层就可以了

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int MAXN=100010;

inline int read(){
    int x=0; char c=getchar();
    while(c<'0') c=getchar();
    while(c>='0') x=(x<<3)+(x<<1)+c-'0',c=getchar();
    return x;
}

int n,m,du[MAXN];
long long Ans;

int Head[MAXN],num;
struct NODE{
    int to,nxt;
}e[MAXN<<1];

inline void add(int x,int y){
    e[++num].to=y;
    e[num].nxt=Head[x];
    Head[x]=num;
}

inline bool lk(int x,int y){
    return du[x]>du[y]||(du[x]==du[y]&&x>y);
}

int vis[MAXN];

int rt;
inline void dfs(int u,int d){
    if(d==0){
        rt=u;
        for(int i=Head[u];i;i=e[i].nxt){
            int v=e[i].to;
            if(lk(rt,v)) dfs(v,d+1);
        }
    }
    else{
        for(int i=Head[u];i;i=e[i].nxt){
            int v=e[i].to;
            if(lk(rt,v)){
                Ans+=vis[v];
                ++vis[v];
            }
        }
    }
}

inline void clr(int u,int d){
    if(d==0){
        rt=u;
        for(int i=Head[u];i;i=e[i].nxt){
            int v=e[i].to;
            if(lk(rt,v)) clr(v,d+1);
        }
    }
    else for(int i=Head[u];i;i=e[i].nxt)
        ++vis[e[i].to]=0;
}

int main(){
    n=read(); m=read();
    int x,y;
    for(int i=1;i<=m;++i){
        x=read(); y=read();
        add(x,y); add(y,x);
        ++du[y]; ++du[x];
    }
    for(int i=1;i<=n;++i){
        dfs(i,0);
        clr(i,0);
    }
    printf("%lld\n",Ans);
    return 0;
}

2019.10.1 qbxt模拟题

标签：ace   两种   span   图片   代码   add   struct   复杂度   第一题   

原文地址：https://www.cnblogs.com/yjkhhh/p/11792848.html