CF519E A and B and Lecture Rooms

https://www.luogu.org/problem/CF519E

https://codeforces.com/problemset/problem/519/E

题目背景

题目描述

给出一棵\(n\)个节点的无根树和\(q\)个询问，每次询问树上到\(x,y\)两节点距离相等的节点个数。

输入格式

略

输出格式

每行对一个询问输出一个答案。

数据范围分析

\(1\le n,q\le10^5\)。

naive的\(O(nlogn)\)。

code

#include<bits/stdc++.h>
inline int abs(int x)
{
    return x>0?x:-x;
}

template<class T>inline T read()
{
    int sign=1;
    T sum=0;
    char c;
    while((c=getchar())<'0'||c>'9')
        if(c=='-')
            sign=-1;
    while(c>='0'&&c<='9')
    {
        sum=(sum<<1)+(sum<<3)+(c^48);
        c=getchar();
    }
    
    return sum*sign;
}

template<class T>inline void write(T x)
{
    if(x<0)
        putchar('-');
    x=abs(x);
    if(x>9)
        write(x/10);
    putchar(x%10+48);
    return;
}

struct node
{
    int to,nxt;
}edge[200001];
int n,m,q,num,head[100001],dep[100001],father[100001][41],size[100001];
inline void add(int u,int v)
{
    edge[num=-~num].to=v;
    edge[num].nxt=head[u];
    head[u]=num;
    return;
}

inline void df1(int last,int s,int d)
{
    dep[s]=d;
    father[s][0]=last;
    size[s]=1;
    for(register int i=1;(1<<i)<=d;i=-~i)
        father[s][i]=father[father[s][i-1]][i-1];
    for(register int i=head[s];i;i=edge[i].nxt)
        if(edge[i].to^last)
        {
            df1(s,edge[i].to,-~d);
            size[s]+=size[edge[i].to];
        }
        
    return;
}

inline int lca(int x,int y)
{
    if(dep[x]<dep[y])
        x^=y^=x^=y;
    for(register int i=16;i>=0;i--)
        if(dep[father[x][i]]>=dep[y])
            x=father[x][i];
    if(!(x^y))
        return y;
    for(register int i=16;i>=0;i--)
        if(father[x][i]^father[y][i])
        {
            x=father[x][i];
            y=father[y][i];
        }
        
    return father[x][0];
}

inline int find(int x,int k)
{
    int res=x;
    for(register int i=16;i>=0;i--)
        if(dep[x]-dep[father[res][i]]<=k)
            res=father[res][i];
    return res;
}

inline int query(int x,int y)
{
    if(!(x^y))
        return n;
    int root=lca(x,y);
    int d=dep[x]+dep[y]-2*dep[root];
    if(d&1)
        return 0;
    d>>=1;
    if(!(d^dep[x]-dep[root]))
        return n-size[find(x,d-1)]-size[find(y,d-1)];
    else if(d<dep[x]-dep[root])
        return size[find(x,d)]-size[find(x,d-1)];
    else
        return size[find(y,d)]-size[find(y,d-1)];
}

int main()
{
    n=read<int>();
    m=n-1;
    for(register int i=1;i<=m;i=-~i)
    {
        int u=read<int>(),v=read<int>();
        add(u,v);
        add(v,u);
    }
    
    df1(0,1,0);
    scanf("%d",&q);
    for(register int i=1;i<=q;i=-~i)
    {
        int x=read<int>(),y=read<int>();
        write<int>(query(x,y));
        putchar('\n');
    }
    
    return 0;
}

solution

树上倍增。

在树上求距离显然和LCA相关。

为方便规定\(1\)为根。

先预处理出\(k\)倍祖先。

然后呢？

有什么方法快速统计满足条件点的个数？

没思路，先画下图看看吧。

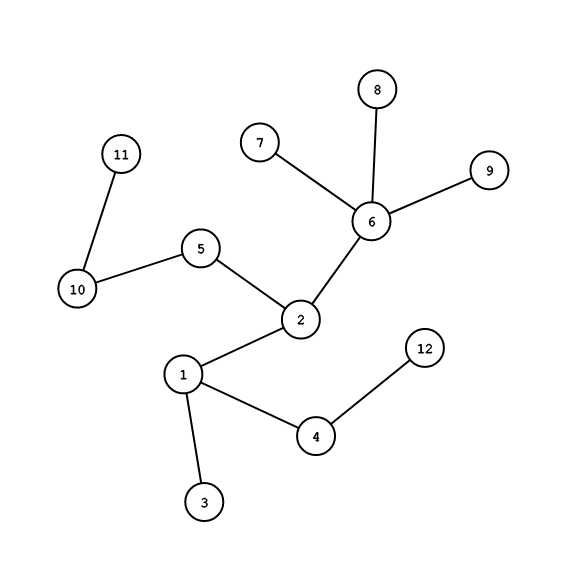
然后呢？

先询问结点\(5,12\)。

乱搞一通发现有\(1,3\)满足到\(5,12\)距离相等。

\(5\)和\(12\)的LCA是\(1\)。

然后呢？

再问一组吧，\(5\)和\(6\)。

LCA是\(2\)，答案是\(5\)。

然后呢？

再问一组：\(1\)和\(7\)。

完了好像找不到。

好像并没有什么规律

然而是有的。

这次我们选择结点\(9,10\)。考虑把图扯一下，这样就更清晰了：

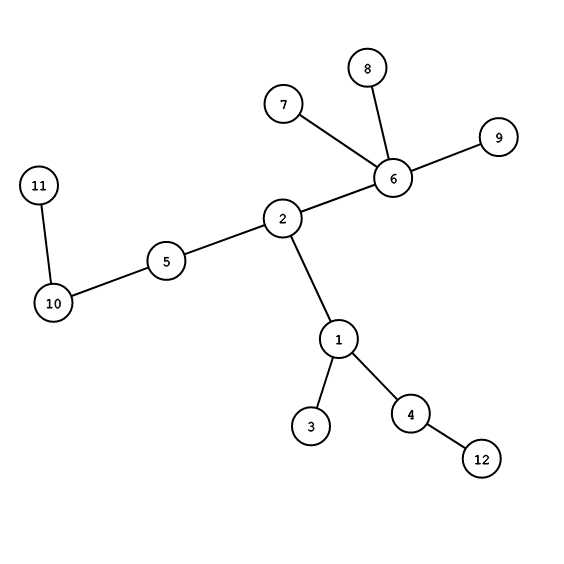
树上任意两点间有且只有一条简单路径，这是众所周知be universally known的。现在图一扯我们就能发现，\(9,10\)之间的路径就是\(9-6-2-5-10\)。显然在路径上除了中点，是不可能有一个满足条件的点的。

又由于从这些不满足条件的点延伸出去的且不在路径上的点到两端点距离之差显然不会变，故像\(7,8\)这类的点也都不行了。

所以\(1\)和\(7\)没办法找到答案。因为它们的路径上没有中点。得中点者得天下。

简而言之，答案就是与中点相连且不在路径上的点的数量。

然后呢？

怎么求？

大致思想是统计去掉所有路径上和路径上非中点延伸出的点之后剩下的点的数目。

然后呢？

如果中点是LCA，那么答案点集就是整棵树砍掉以两点为根的两棵子树。

如果不是LCA呢？感性考虑一下，假设中点在LCA左边，那么以左边的点为根的那棵子树显然都要砍掉。不仅如此，从中点往上走的部分也都要砍掉。那么我们发现答案点集就是“以中点为根的子树砍掉以中点在中点到询问点的路径上的儿子为根的子树”。如\(4,9\)，中点\(2\)，\(2\)的子树为\(\{2,5,10,11,6,9,7,8\}\)，\(2\)的儿子\(6\)的子树为\(\{6,7,8,9\}\)，故答案点集为\(\{2,5,10,11\}\)。

然后子树大小这个东西也是可以在处理深度和祖先时一起预处理出来的。时间复杂度\(O(qlogn)\)。