标签:+= RoCE head 路径修改 目的 upd 最大的 gets 最大
树链剖分的基本思想是把一棵树剖分成若干条链,再利用线段树等数据结构维护相关数据,可以非常暴力优雅地解决很多问题。
树链剖分中的几个基本概念:
重儿子:对于当前节点的所有儿子中,子树大小最大的一个儿子就是重儿子(子树大小相同的则随意取一个)
轻儿子:不是重儿子就是轻儿子
重边:连接父节点和重儿子的边
轻边:连接父节点和轻儿子的边
重链:相邻重边相连形成的链
值得注意的还有以下几点:
叶子节点没有重儿子也没有轻儿子;
对于每一条重链,其起点必然是轻儿子;
单独一个轻叶子节点也是一条重链;
结合上面三条可以得出树剖的一个性质:重链必然可以囊括所有的节点。
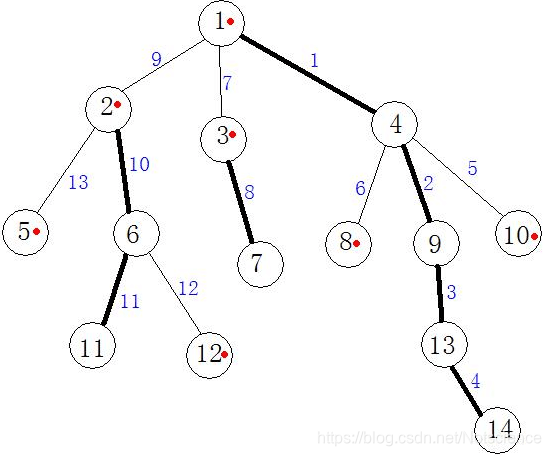
(图片来源百度图片,侵删)
红点标记的是轻儿子,粗线就是重链。结合图片理解概念。
树链剖分需要怎么做呢?
1、用DFS给每一个节点标记深度,父节点和重儿子。
2、用DFS按照DFS遍历的顺序给每一个节点标记新的编号。关键点:先处理重儿子再处理轻儿子
解释:先处理重儿子可以让重链上的每一个点的编号连续。可以观察上图,线上的数字就是DFS的顺序。使编号连续后,我们就可以使用线段树来维护数据了。
做完以上两步就算是完成了树链剖分了,接下来要做的就是利用其它数据结构来进行维护了。
void add(ll sta,ll to)
{
edge[++cnt].to=to;
edge[cnt].next=head[sta];
head[sta]=cnt;
}//链式前向星存树
void dfs1(ll now,ll fa,ll deep)
{
f[now]=fa;//记录父节点
d[now]=deep;//记录深度(深度在区间求和时会用到)
size[now]=1;//记录子树大小
for (ll i=head[now];i!=0;i=edge[i].next)
{
if (edge[i].to==fa) continue;
dfs1(edge[i].to,now,deep+1);
size[now]+=size[edge[i].to];
if (size[edge[i].to]>size[wson[now]]) wson[now]=edge[i].to;
//取重儿子
}
}
void dfs2(ll now,ll t)
{
top[now]=t;//记录节点所在重链的起点
id[now]=++cnt;//按照顺序编号
rk[cnt]=now;//记录第cnt个点表示的是now节点,建树时会用到
if (wson[now]) dfs2(wson[now],t);//优先处理重儿子
for (ll i=head[now];i!=0;i=edge[i].next)
{
if (edge[i].to==wson[now]) continue;
if (edge[i].to==f[now]) continue;
dfs2(edge[i].to,edge[i].to);//一条重链的开头必然是轻儿子,链头即为它本身
}
}树上两点的最短路径修改操作:
void treeupd(ll x,ll y,ll num)
{
while (top[x]!=top[y])
{
if (d[top[x]]>d[top[y]])
{
segupd(1,1,n,id[top[x]],id[x],num);
//segupd为线段树的更新函数
x=f[top[x]];
}
else
{
segupd(1,1,n,id[top[y]],id[y],num);
//segupd为线段树的更新函数
y=f[top[y]];
}
}
//这一个循环的目的是,只要这两个节点不在一条重链上,
//就让比较深的那一个往上跳到另一条链直到两者在同一条链上
//又因为节点编号是连续的,所以可以很方便地给整条链加上修改操作
if (id[x]<=id[y]) segupd(1,1,n,id[x],id[y],num);
else segupd(1,1,n,id[y],id[x],num);
//在最后两者位于同一条链上后,仍然要对他们两个之间的节点进行修改。
}求和操作不再赘述,与上面的更新操作类似。
完整代码
#include<cstdio>
#include<algorithm>
#define lson root<<1
#define rson root<<1|1
#define ll long long
#define mid ((l+r)>>1)
using namespace std;
struct data
{
ll to,next;
}edge[200005];
ll cnt,head[200005],f[100005],d[100005],size[100005],wson[100005],top[100005],id[100005];
ll rk[100005],tree[800005],n,m,a[100005],p,tag[800005],r,x,y,z,flag;
void add(ll sta,ll to)
{
edge[++cnt].to=to;
edge[cnt].next=head[sta];
head[sta]=cnt;
}
void dfs1(ll now,ll fa,ll deep)
{
f[now]=fa;
d[now]=deep;
size[now]=1;
for (ll i=head[now];i!=0;i=edge[i].next)
{
if (edge[i].to==fa) continue;
dfs1(edge[i].to,now,deep+1);
size[now]+=size[edge[i].to];
if (size[edge[i].to]>size[wson[now]]) wson[now]=edge[i].to;
}
}
void dfs2(ll now,ll t)
{
top[now]=t;
id[now]=++cnt;
rk[cnt]=now;
if (wson[now]) dfs2(wson[now],t);
for (ll i=head[now];i!=0;i=edge[i].next)
{
if (edge[i].to==wson[now]) continue;
if (edge[i].to==f[now]) continue;
dfs2(edge[i].to,edge[i].to);
}
}
void build(ll root,ll l,ll r)
{
if (l==r)
{
tree[root]=a[rk[l]]%p;
return ;
}
build(lson,l,mid);
build(rson,mid+1,r);
tree[root]=(tree[lson]+tree[rson])%p;
}
void push_down(ll root,ll l,ll r)
{
if (tag[root]==0) return ;
tag[lson]+=tag[root];
tag[rson]+=tag[root];
tree[lson]+=tag[root]*(mid-l+1);
tree[rson]+=tag[root]*(r-mid);
tag[lson]%=p;
tag[rson]%=p;
tree[lson]%=p;
tree[rson]%=p;
tag[root]=0;
}
void segupd(ll root,ll l,ll r,ll al,ll ar,ll num)
{
if (ar<l||r<al) return ;
if (al<=l&&r<=ar)
{
tree[root]+=num*(r-l+1);
tag[root]+=num;
tree[root]%=p;
tag[root]%=p;
return ;
}
push_down(root,l,r);
segupd(lson,l,mid,al,ar,num);
segupd(rson,mid+1,r,al,ar,num);
tree[root]=(tree[lson]+tree[rson])%p;
}
ll query(ll root,ll l,ll r,ll al,ll ar)
{
if (ar<l||r<al) return 0;
if (al<=l&&r<=ar) return tree[root]%p;
push_down(root,l,r);
return (query(lson,l,mid,al,ar)+query(rson,mid+1,r,al,ar))%p;
}
ll getsum(ll x,ll y)
{
ll sum=0;
while (top[x]!=top[y])
{
if (d[top[x]]>d[top[y]])
{
sum=(sum+query(1,1,n,id[top[x]],id[x]))%p;
x=f[top[x]];
}
else
{
sum=(sum+query(1,1,n,id[top[y]],id[y]))%p;
y=f[top[y]];
}
}
if (id[x]<=id[y]) sum=(sum+query(1,1,n,id[x],id[y]))%p;
else sum=(sum+query(1,1,n,id[y],id[x]))%p;
return sum;
}
void treeupd(ll x,ll y,ll num)
{
while (top[x]!=top[y])
{
if (d[top[x]]>d[top[y]])
{
segupd(1,1,n,id[top[x]],id[x],num);
x=f[top[x]];
}
else
{
segupd(1,1,n,id[top[y]],id[y],num);
y=f[top[y]];
}
}
if (id[x]<=id[y]) segupd(1,1,n,id[x],id[y],num);
else segupd(1,1,n,id[y],id[x],num);
}
int main()
{
scanf("%lld%lld%lld%lld",&n,&m,&r,&p);
for (ll i=1;i<=n;i++)
scanf("%lld",&a[i]);
for (ll i=1;i<n;i++)
{
scanf("%lld%lld",&x,&y);
add(x,y);
add(y,x);
}
cnt=0;
dfs1(r,0,0);
dfs2(r,r);
build(1,1,n);
for (ll i=1;i<=m;i++)
{
scanf("%lld",&flag);
if (flag==1)
{
scanf("%lld%lld%lld",&x,&y,&z);
treeupd(x,y,z);
}
if (flag==2)
{
scanf("%lld%lld",&x,&y);
printf("%lld\n",getsum(x,y));
}
if (flag==3)
{
scanf("%lld%lld",&x,&z);
segupd(1,1,n,id[x],id[x]+size[x]-1,z);
//这里可以结合图片理解一下为什么。
}
if (flag==4)
{
scanf("%lld",&x);
printf("%lld\n",query(1,1,n,id[x],id[x]+size[x]-1));
}
}
return 0;
} 标签:+= RoCE head 路径修改 目的 upd 最大的 gets 最大
原文地址:https://www.cnblogs.com/notscience/p/11798342.html