标签:没有 不能 很多 排序算法 table 题目 有一个 最小值 最短路算法
CSP2019第一轮还有1天临时抱一波佛脚
update in 2019.10.17
update in 2019.10.18
int A[100],n;
int main() {
cin>>n;
for(int i = 1; i <= n; ++i) {
A[0]++;
int now=0;
while(A[now] == 2) {
A[now] = 0;
A[++now]++;
}
}
}A.O(n) B.O(nlogn) C.O(n^2) D.O(n sqrt(n))
答案:A
解析:可以理解成是一颗二叉树一层一层合并,每个i都在底部增加一个新节点,如果可以合并,就自动合并。一直合并到一颗有n个叶子节点的满二叉树,二叉树的每一层分别是n,n/2,n/4,n/8,...,1。
也可以理解为模拟二进制加一运算,和二叉树是同一个道理。
二进制加一运算:
| i | A |
|---|---|
| 1 | 1 |
| 2 | 01 |
| 3 | 11 |
| 4 | 001 |
二叉树合并:

A.6 7 B.4 5 C.4 12 D.1 7
答案:A
解析:显然x^x==0,所以出现过偶数次的数全部都会变成0,所以只用考虑出现奇数次的,也就是只用考虑两个数。
A.该图是有向图。
B.该图是强联通的。
C.该图所有顶点的入度之和减所有顶点的出度之和等于 1。
D.从 v1 开始的深度优先遍历所经过的顶点序列与广度优先的顶点序列是相同的。
答案:ABD
解析:这道题考了好几次,都写错了。
强连通图(StronglyConnectedGraph)是指在有向图G中,如果对于每一对vi、vj,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。
题目里斜体的那句话一定要注意,它表明了遍历的顺序,使得D选项是正确的。
A.C 语言 B.Pascal C.C++ D.Java
答案:AB;
解析:
面向对象:simula67,c++,java,c#...
面向过程 C,Fortran,Pascal...
解释型:Python,JavaScript,Perl,Shell...
编译型:C,C++,Pascal,Object Pascal...
每张试卷必考题,经常搞混。
int F(int n) {
if (n <= 2)return 1;
else return F(n - 1) + F(n - 2);
}答案:F(n)
解析:
将递归转换为递推,F(1)要算1次,F(2)要算1次,F(3)要算2次……F(n)要算F(n-1)+F(n-2)次,也就是F(n).
计算时间复杂度毒瘤题,挺考察思维
A. 1/2 B. 5/8 C. 1 D. 3/4
答案:D
解析:暴力模拟4!种情况计算 其实只要考试时间够的话可以尝试。
当你发现对方是随机的时候,你采取的策略似乎没什么卵用,和随机是一样的。令对方的次数为a,b,c,你的为i,j,k。答案就是 (ib+jc+ka–aj-bk-ci)/(a+b+c)。快速猜答案方法:局数是 4 ,所以答案的分母一定是 4
A. int *B=A;B++;*B++;
B. int &B=*(A+1);B++;
C. int *B=A;B++;B[0]++;
D. int &B=A+1;B++;
答案:BC
C++语言中指针、取地址的运用,考的不是很多,但每次都错。。
A的话是优先级问题,*B++ 的意思是 *(B++),不是(*B)++ 。
D的话无法编译,平时定义时加上取地址符后面赋值的都是具体的变量,而不是一个地址。A+1虽然表示的是A[1],但实际上表达的是A[1]的地址,所以scanf里面才可以写scanf("%d",A+1)而不加&。
A.14 B.16 C.17 D.19
答案C:鸽巢原理(抽屉原理)
好像也考了两次,第一次没写出来,第二次蒙对。。。
设一次出队的数为 a1 , a2 , a3 , a4 , a5 , … , an
设出队的数前缀和为 b1 , b2 , b3 , b4 , b5 , … , bn ,bn = ∑ai <= 28
需要存在 bi - bj = 6 的 i,j (注意j可以等于0)
差值为6的分成一组
{0,6,12,18,24}最多可以取2个 (因为b[0]=0必然存在的,所以0必取且不计个数)
{1,7,13,19,25}最多可以取3个
{2,8,14,20,26}最多可以取3个
{3,9,15,21,27}最多可以取3个
{4,10,16,22,28}最多可以取3个
{5,11,17,23}最多可以取2个
最后再取一个必然存在某一组差值为6
故答案为 2+3+3+3+3+2+1=17
好题!!!!!
A.18 B.16 C.20 D.8
答案:B 二分图。
无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
A.11520 B.1920 C.240 D.1440
答案:A 容斥原理
A(5,5):DEFGH全排
A(6,3):把ABC插入(插板法)
A(2,2):DE可以交换
A(4,4):(DE)FGH全排(捆绑法)
A(5,3):把ABC插入
A(5,5) * A(6,3) - A(2,2) * A(4,4) * A(5,3)
(ABC不相邻,DE可能相邻) - (ABC不相邻,DE相邻)
很好的一道组合题,综合了很多常用技巧。
A.1/2 B.1/3 C.2/3 D.3/5
答案:B
解析:这种题想要求正解一般是不太可能的,都要用到一些玄学数学知识。考试时可以用排除法。显然如果固定一个点在线段的最左侧,那么以这两个点为端点的线段的期望长度一定是1/2。那在让一个点移动,答案一定小于1/2,所以选项里就只有B了。
#include<iostream>
using namespace std;
int pool[1000],n;
void Solve(int *a) {
cout<< *a << ' ';
swap( a[0], a[1]);
swap( pool[0], pool[2]);
}
int main() {
int *a= pool;
cin >> n;
for ( int i = 0; i < n; ++i)
cin >> pool[i];
cout << *a << ' ';
cout << *a++ << ' ';
cout << *pool << ' ';
cout << *++a << ' ';
Solve(a);
cout << *++a << '\n';
for(int i=0;i<n;i++)cout<<pool[i]<<" ";
cout<<endl;
return 0;
}读入:
4
1 2 3 4
答案:
1 1 1 3 3 3
4 2 1 3
再来一道指针题。还是错了。。。
怎么会有指针这么烦人的东西
题目略有改动。
可以到我的另一篇文章看看,记得回来
A.Cn表示有n+1个节点的不同形态的二叉树的个数。
B.Cn表示含n对括号的合法括号序列的个数。
C.Cn表示长度为n的入栈序列对应的合法的出栈序列个数。
D.Cn表示通过连接顶点而将n+2边的凸多边形分成三角形的方法数。
答案:A
解析:
Cn表示有n个节点的不同形态的二叉树的个数。
卡特兰数,经常考到,曾出现在很多种题里。
公式: \(C_n\)=\(\frac{1}{n+1}\) * \(C^n_{2n}\)
用途:差不多就是上面这些了。
A.1:2 B.2:1 C.1:3 D.1:1
答案:D
解析:一道很有想法的题,考虑如果某个人抽中蓝球,就让他的儿子去抽球,那么每个人抽中红球蓝球的概率相等,那么答案为1:1。
A.当图中不存在负权回路但是存在负权边时,Dijkstra算法不一定能求出源点到所有点的最短路。
B.当图中不存在负权边时,调动多次Dijkstra算法能求出每对顶点间最短路径。
C.图中存在负权回路时,调用一次Dijkstra算法也一定能求出源点到所有点的最短路。
D.当图中不存在负权边时,调用一次Dijkstra算法不能用于每对顶点间的最短路计算。
答案:ABD
解析:对Dijkstra算法的理解。
Dijkstra算法有每次从所有点中找到里源点最近的那个点的贪心策略,但当存在负边权是就不成立了,因为可能有一个点经过了一条非最短的正边,一条负边,结果到源点的距离反而最小。同理,负权回路就更不可能了。
这对于复赛也很重要。
A.?快速排序 B.堆排序 C.希尔排序 D.?插入排序
答案:D
解析:考排序。
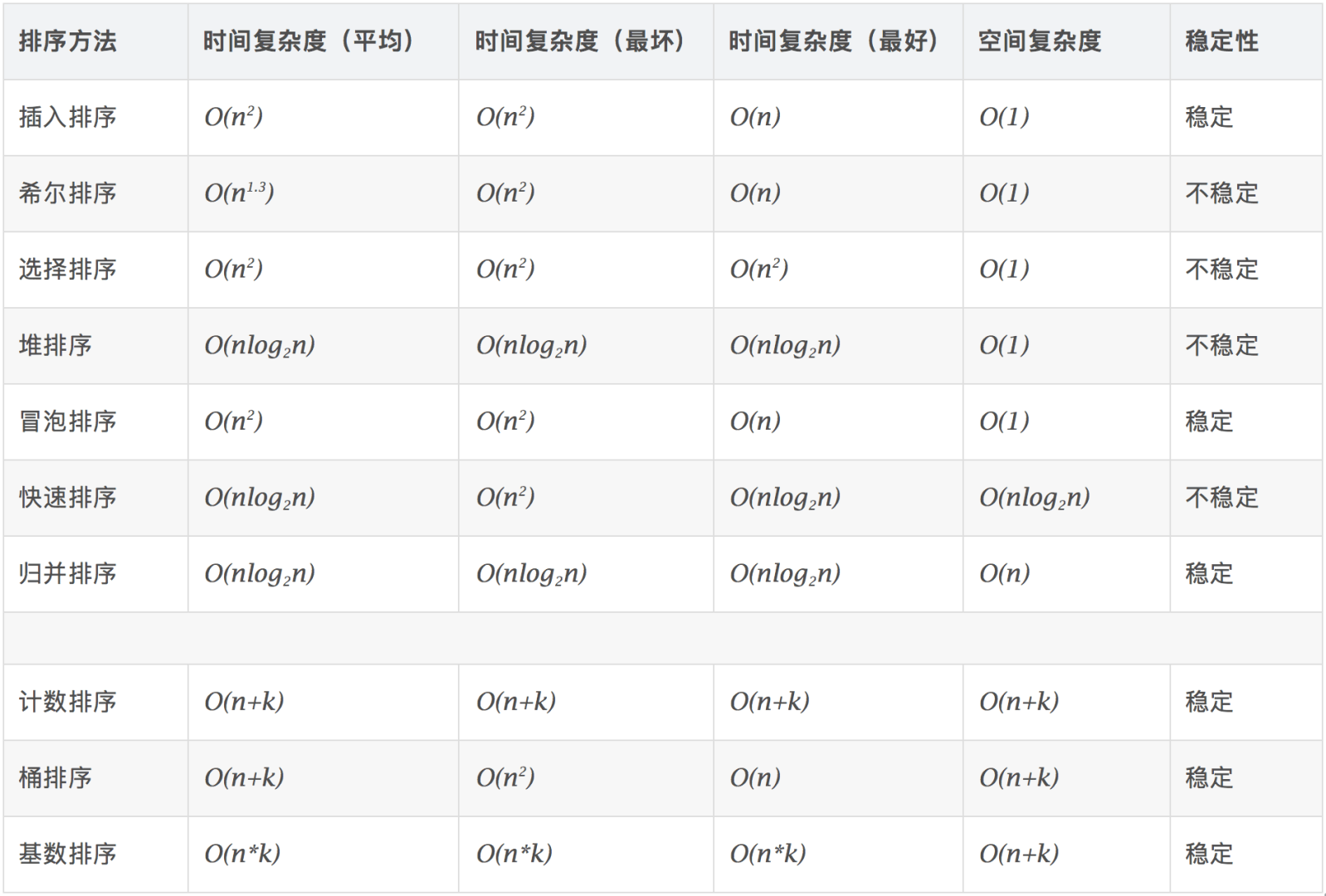
背理解一下就好了。
#include <iostream>
using namespace std;
int main()
{
int n, m;
cin >> n >> m;
int x = 1;
int y = 1;
int dx = 1;
int dy = 1;
int cnt = 0;
while (cnt != 2)
{
cnt = 0;
x = x + dx;
y = y + dy;
if (x == 1 || x == n)
{
++cnt;
dx = -dx;
}
if (y == 1 || y == m)
{
++cnt;
dy = -dy;
}
}
cout << x << " " << y << endl;
return 0;
}输入 1:4 3
答案:1 3
输入 2:2017 1014
答案: 2016 1
输入 3:987 321
答案: 1 321
解析:一道比较难的程序阅读题。第一个数据可以模拟出来,后面两个就需要读懂它在干嘛了。
第一次在普及组写这道题时没看见每次cnt=0的清空。。。
类似于打台球,或者说找最小公倍数,但要注意是从(1,1)开始的,所以对所给的输入都要先减一。
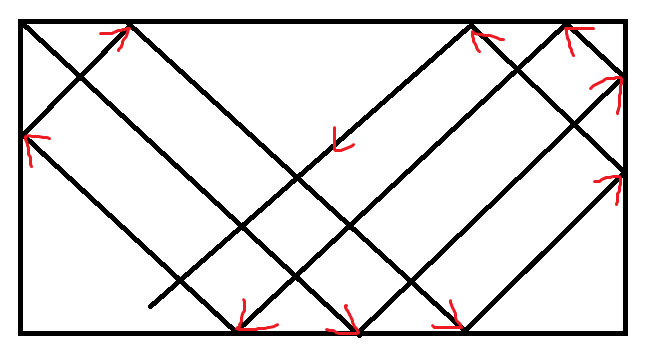
如图,从左上角的(1,1)开始,遇到边就反弹,知道射到矩形的四个角之一为止。
发现这个后就可以用小学奥数的一些常用技巧,比如把这个矩形对称翻折,求最小公倍数
但是发现题目里还有一个坑,直接将这个矩形的两边设为 n,m 的话是错的,得变为 n-1,m-1 。
以后找到方法后可以带进小样例看一看,是不是正确的。
A 5 B 0 C 8 D 4
答案:A
解析:考运算符优先级 恶心

背一下就好了
可以到我的另一篇文章里看看,记得回来
答案:256。
解析:鸽巢原理。
有一句很关键的话: 如果无论 p,q,r 如何取值,两个布尔表达式的值总是相同,则称它们等价。
p,q,r每个数都可以取1或0,总共有8种取法。每一种取法的表达式值为0或1。
因此每个表达式可以等价于一个8位的01字符串,对应表达式 p , q , r 的8种取法的结果。
总共有2^8个不同的串(从8个0到8个1),且这2^8个串没有一个串是完全相同的,即没有两个表达式的值相同。
所以一共有\(2^8\)个两两不等价的布尔表达式。
答案:60
解析:就是一个放苹果问题,允许有空盘子。
先不考虑鸽子不回来的情况,用 f(i,j)表示 i 只鸽子,j 个鸽舍。则
f( i , j ) = f( i , j - 1 ) + f( i - j , j ) (i >= j)
f( i , j - 1 ) : 因为如果有空鸽舍,则删掉空鸽舍,将方案数转移。
f( i - j , j ) : 如果没有空鸽舍,则先将这 j 个鸽舍都放上一只鸽子。
如果鸽子数小于鸽舍数,则 f( i , j ) = f( i , i ).
初始状态 f(0,1)=1,f(0,0)=1.
然后答案等于 ∑ f(i,5) (i=0,1,……,8)
这类问题大多都可以考虑插板法。
一般只要出题人有点良心都是可以枚举的
第二类斯特林数:
S(n,m) 表示有n个有区别小球,要放进m个相同盒子里,且每个盒子非空的方案数
考虑一个很容易的递推:
S(n,m) = S(n?1,m?1) + m l? S(n?1,m)
考虑组合意义:
假设前面的n?1个球丢进了m?1个组,因为每个组非空,所以这个球只有一种选择自己一组
如果前面的球已经分成了m组,那么,这个球就有m种放法
所以这个递推式就是这样来的
每个小球有m种选择,所以就是 \(m^n\) 种。
好像要用什么玄学方法。。还是枚举比较好
答案:\(C_7^4\) * \(A_4^4\) = \(A_7^4\)
解析:排列组合题。只要想到了方法就很简单
想象一下有7把椅子,先让除甲乙丙的四个人去挑四把椅子,共有 \(C_7^4\) * \(A_4^4\) 种方法。然后剩下的三把椅子甲乙丙只有一种坐法,所以答案就是 \(C_7^4\) * \(A_4^4\)。
假设有递推关系式 \(T(n)=aT( \tfrac{n}{b} )+f(n)\) 其中 n 为问题规模,a 为递推的子问题数量,\(\tfrac{n}{b}\) 为每个子问题的规模(假设每个子问题的规模基本一样),\(f(n)\) 为递推以外进行的计算工作。

看着就不想写
其实还是比较好记的,就是先把 a,b 求出来,然后判断一下\(f(n)\)与\(n^{log_ba}\)的大小:
if ( \(f(n) == n^{log_ba} * log^kn\) ),那么\(T(n)\)就是\(O(n^{log_ba} * log^{k+1}n)(k>=0)\)
(update in 10.16 ,这是上面那个链接里的内容,百度百科上的不全面)
else if ( \(f(n) < n^{log_ba}\) ), 那么\(T(n)\)就是\(O(n^{log_ba})\)
else if(\(f(n)>n^{log_ba}\)),那么\(T(n)=f(n)\)
大概是这样的,有些复杂的情况在这里没有涉及,估计也考不到
例题:
1.若某算法的计算时间表示为递推关系式:
\(T(n)=4T( \tfrac{n}{2} )+\sqrt{n}\)
\(T(1)=1\)
则该算法的时间复杂度为( )
答案:\(O(n^2)\)
解析:易得 a = 4,b = 2 。所以\(log_ba=2,n^{log_ba}=n^2 > \sqrt{n}\) , 所以\(T(n)=O(n^2)\) 。
2.【NOIP2017初赛】若某算法的计算时间表示为递推关系式:
\(T(N)=2T(\tfrac{N}{2})+NlogN\),\(T(1)=1\),则该算法的时间复杂度为
A.\(O(N)\) B.\(O(Nlog_2N)\) C.\(O(Nlog_2^2N)\) D.\(O(N^2)\)
答案:C
解析:易得 a = 2,b = 2,\(f(N)=NlogN=N^{log_ba} * logN\),k=1,所以是第一种情况,\(T(N)=O(Nlog_2^2N)\) 。
用 markdown 打数学公式好麻烦啊。。。

答案:37/12
解析:一道曾经非常厌恶的期望题 现在也有点,
设从2跳到1的期望是\(f2\),那么有1/2的概率是一次跳到1,还有1/2的概率是(1+f2)次跳到1,即第一次没有跳到1,跳到2的情况,于是可以列出等式:
\(f2=1 * 1/2+(1+f2) * 1/2\), 得\(f2=2\);
对于n=3,则有1/3的概率一次跳到1,有1/3的概率\((1+f2)\)次跳到1,即第一次跳到2,再从2跳到1的过程,最后还有1/3的概率\((1+f3)\)次跳到1,于是
\(f3=1/3+(1+f2) * 1/3+(1+f3) * 1/3\), 得\(f3=2.5\);
同理得\(f4,f5\) ,答案即为 \(f5\);
其实还可以整理出递推公式,但我因为太懒就不打了。。
对于这种期望的题,一般都得列方程,不然会涉及到很多关于无限的东西(逃
A.47/72 B.39/72 C.25/36 D.3/5
答案:A
解析:
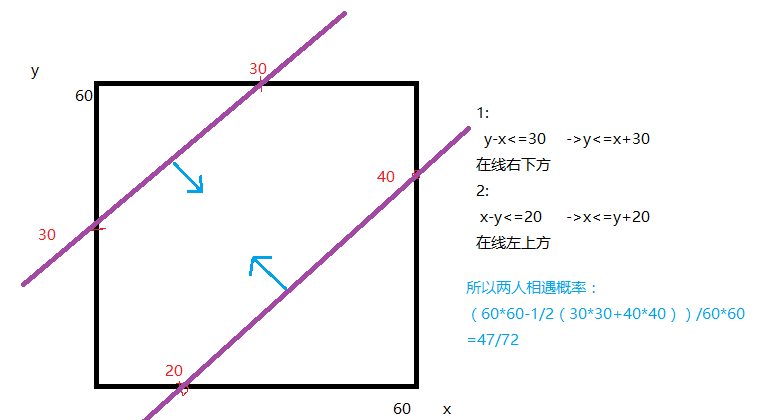
这种不是很好想的题,画图往往有想不到的功效。
答案:2/3
解析:b赢的线路更清晰一些,所以我们分析b赢的概率。
发现两个都需要H作为开头,那么令f(x)为开头是H的b赢的概率.
那么有1/2下一个是T,并且有1/2*1/2是b直接获胜,或者重新回到H开头.
可以列出方程:\(1/4+1/4 * f(x)=f(x)\)
解得 \(f(x)=1/3\),那么a获胜的概率就是2/3

好题! 考试的时候是从小a分析的,不知道怎么就算错了,应该挑一个简单一点的分析。
#include <iostream>
using namespace std;
const int SIZE = 20;
int data[SIZE];
int n, i, h, ans;
void merge( ) {
data[h - 1] = data[h - 1] + data[h];
h--;
ans++;
}
int main( ) {
cin >> n;
h = 1;
data[h] = 1;
ans = 0;
int mx=1;
for (i = 2; i <= n; i++) {
h++;mx=max(mx,h);
data[h] = 1;
while (h > 1 && data[h] == data[h - 1])
merge( );
for(int i=1;i<=mx;i++)cout<<data[i]<<" ";
cout<<endl;
}
cout << ans << endl;
}输入:8
输出:______ 答案:7
输入:2012
输出:______ 答案:2004
考过一遍,几个星期后又忘了。。。
挺好的一道题,可以从二叉树的角度考虑。
对于第一个小样例,模拟一下:
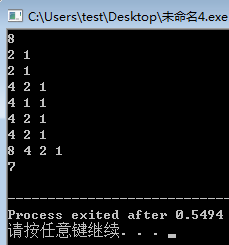
接下来把它变一下形(二叉树):
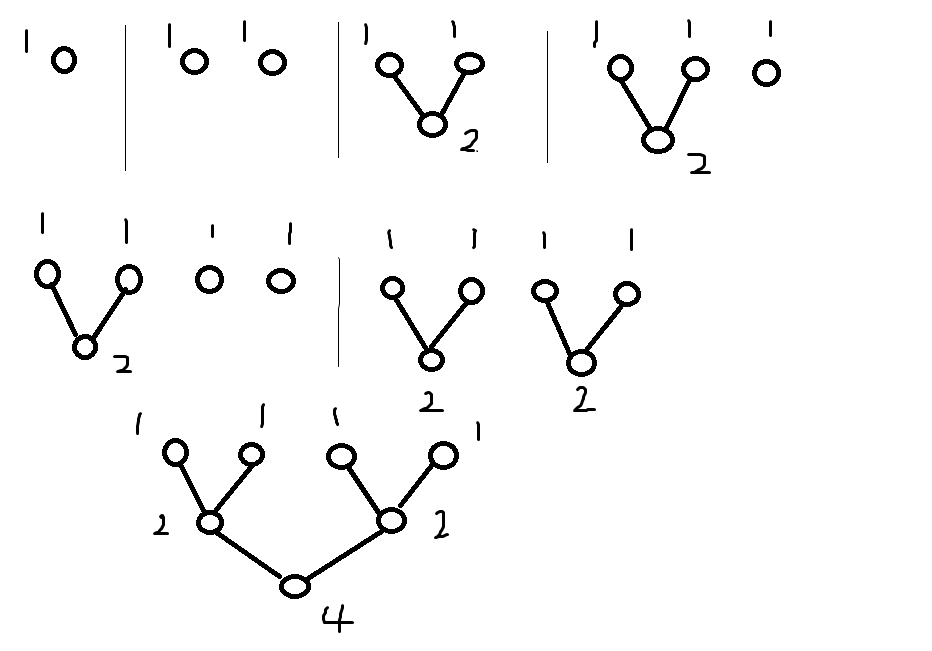
貌似有点眼熟
仔细一看,发现这两个好像真的是同一个东西:
然后就很简单了。
【恍然大悟】
可以到我的另一篇文章看看,记得回来
A.(8,3) B.(5,5) C.(1,4) D.(19260817,20020331)
答案:ABCD
解析:
假设先手先取最右上角,如果后手有办法进入先手必胜,那么A就可以抢先进入先手必胜。
所以只要后手能赢,那先手必赢,则除了(1,1)之外先手永远有必胜策略 显然(1,1)也有 tql
刚好30题,再也不更了 真香
标签:没有 不能 很多 排序算法 table 题目 有一个 最小值 最短路算法
原文地址:https://www.cnblogs.com/tangzhiyang/p/11799250.html