程序员面试题100题（一）(转)

标签：max   最简   数列   公式   面试题   它的   print   出现   word   

题目选自以下博客网址：
http://zhedahht.blog.163.com/#。

第26题：
题目：输入一个正数n，输出所有和为n连续正数序列。

例如输入15，由于1+2+3+4+5=4+5+6=7+8=15，所以输出3个连续序列1-5、4-6和7-8。

我自己的思路：
首先想到的是等差数列的求和，即(m1+(m1+k-1))*k=n*2,  其中起始数字start=m1,结束数字end=m1+k-1;
因此这道题目的解和n*2的因子有关，解的集合在2n的在 [2，sqrt(2n)] 区间的几个因子相关。每个因子可能对应一个解，但是也可能这个因子没有解。

当n=30000时，输出结果如下：

9999-10001
5998-6002
1993-2007
1188-1212
922-953
363-437
265-360
178-302
108-267

我觉得它的好处是代码量较少，清晰易读。


————————————————————————————————————————
第23题：跳台阶问题
题目：一个台阶总共有n级，如果一次可以跳1级，也可以跳2级。求总共有多少总跳法，并分析算法的时间复杂度。

首先我们考虑最简单的情况。如果只有1级台阶，那显然只有一种跳法。如果有2级台阶，那就有两种跳的方法了：一种是分两次跳，每次跳1级；另外一种就是一次跳2级。

现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。

我们把上面的分析用一个公式总结如下：

        /  1                          n=1
f(n)=      2                          n=2
        \  f(n-1)+(f-2)               n>2

分析到这里，相信很多人都能看出这就是我们熟悉的Fibonacci序列。

问题的解，是一个树形结构，我引入了TreeView中的节点TreeNode来成生这个树，它是一个典型递归：

树组装好以后，每一个叶子节点的全路径就是一个解，因此将叶子节点的FullPath（路径）打印出来即为一个解，这里为了找到叶子节点，也是使用递归：

当输入n=5时，打印出所有叶子节点的FullPath如下：

root\1\1\1\1\1
root\1\1\1\2
root\1\1\2\1
root\1\2\1\1
root\1\2\2
root\2\1\1\1
root\2\1\2
root\2\2\1

我们可以把一个解在一个TreeView里面完整显示出来：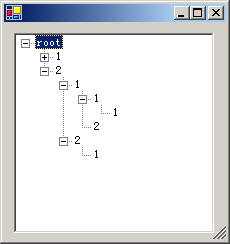


递归算法有一个很受限制的地方，它占用栈空间以深度的级数速度增长，如果深度太大，会迅速达到空间上限。因此只适合较浅深度求解。

程序员面试题100题（一）(转)

标签：max   最简   数列   公式   面试题   它的   print   出现   word   

原文地址：https://www.cnblogs.com/xyy2019/p/11806919.html