标签:style blog class c ext color
在这一节,我们用MCMC框架来考察几个例子。
一、和共轭凸函数的关系
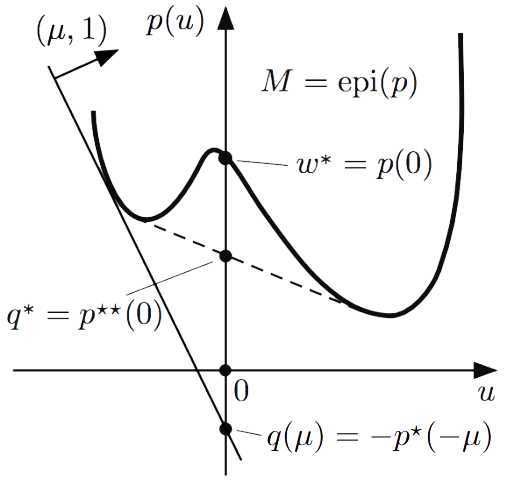 设MM
设MM 是函数p: \mathbb{R}^n \mapsto [-\infty,
\infty]p:R
是函数p: \mathbb{R}^n \mapsto [-\infty,
\infty]p:R n
n ?[?∞,∞]
?[?∞,∞] 的上境图,易知此时有\begin{align*} w^* = p(
\boldsymbol{0} ) \end{align*}
的上境图,易知此时有\begin{align*} w^* = p(
\boldsymbol{0} ) \end{align*}
且\begin{align*} q(\boldsymbol{\mu}) =
\inf_{(\boldsymbol{u} ,w) \in epi(p)} \{ w + \boldsymbol{\mu}^\top
\boldsymbol{u} \} = \inf_{ \{ (\boldsymbol{u} ,w) |
p(\boldsymbol{u} ) \leq w \} } \{ w + \boldsymbol{\mu}^\top
\boldsymbol{u} \}, \end{align*}
将w
用p(\boldsymbol{u} )
替换可得\begin{align*} q(\boldsymbol{\mu}) =
\inf_{ \boldsymbol{u} \in \mathbb{R}^n } \{ p(\boldsymbol{u} ) +
\boldsymbol{\mu}^\top \boldsymbol{u} \} = - \sup_{
\boldsymbol{u} \in \mathbb{R}^n } \{ (-\boldsymbol{\mu})^\top
\boldsymbol{u} - p(\boldsymbol{u} ) \} = -p^*(-\boldsymbol{\mu}).
\end{align*}
于是\begin{align*} q^* =
\sup_{\boldsymbol{\mu} \in \mathbb{R}^n} q(\boldsymbol{\mu}) =
\sup_{\boldsymbol{\mu} \in \mathbb{R}^n} \{ 0 \cdot (- \boldsymbol{\mu}) -
p^*(-\boldsymbol{\mu}) \} = p^{**}( \boldsymbol{0} ), \end{align*}
由此易知,若p = p^{**}
(即p
是正常闭凸函数),则有w^* = q^*
,如右图所示。
二、一般的对偶优化
考虑最小化函数f: \mathbb{R}^n \mapsto [-\infty,
\infty]
,引入函数F: \mathbb{R}^{n+r} \mapsto [-\infty,
\infty]
使得\begin{align} \label{equ: general
optimization duality f} f(\boldsymbol{x}) = F(\boldsymbol{x},
\boldsymbol{0} ), \ \forall \boldsymbol{x} \in \mathbb{R}^n.
\end{align}
设函数p: \mathbb{R}^r \mapsto [-\infty,
\infty]
定义如下:\begin{align} \label{equ: general
optimization duality p} p(\boldsymbol{u} ) = \inf_{\boldsymbol{x} \in
\mathbb{R}^n} F(\boldsymbol{x},\boldsymbol{u}), \end{align}
这里\boldsymbol{u}
可以看成是一个扰动项,p(\boldsymbol{u} )
是原函数经过扰动后的最优解,当\boldsymbol{u} =
\boldsymbol{0}
时,p( \boldsymbol{0} )
就是原函数的最优解,因为显然有\begin{align*}
p(\boldsymbol{0} ) = \inf_{\boldsymbol{x} \in \mathbb{R}^n}
F(\boldsymbol{x}, \boldsymbol{0} ) = \inf_{\boldsymbol{x} \in
\mathbb{R}^n} f(\boldsymbol{x}). \end{align*}
设M
是p
的上境图,易知此时有\begin{align*} w^* = p(
\boldsymbol{0} ) = \inf_{\boldsymbol{x} \in \mathbb{R}^n}
F(\boldsymbol{x}, \boldsymbol{0} ) = \inf_{\boldsymbol{x} \in
\mathbb{R}^n} f(\boldsymbol{x}). \end{align*}
且\begin{align*}q(\boldsymbol{\mu}) =
\inf_{(\boldsymbol{u} ,w) \in epi(p)} \{ w + \boldsymbol{\mu}^\top
\boldsymbol{u} \} = \inf_{ \{ (\boldsymbol{u} ,w) |
p(\boldsymbol{u} ) \leq w \} } \{ w + \boldsymbol{\mu}^\top
\boldsymbol{u} \} = \inf_{ \boldsymbol{u} \in \mathbb{R}^r }
\{ p(\boldsymbol{u} ) + \boldsymbol{\mu}^\top \boldsymbol{u}\},
\end{align*}
将p(\boldsymbol{u} )
用F(\boldsymbol{x}, \boldsymbol{u}
)
替换可得\begin{align*} q(\boldsymbol{\mu})
= \inf_{ (\boldsymbol{x}, \boldsymbol{u} ) \in \mathbb{R}^{n+r} } \{
F(\boldsymbol{x}, \boldsymbol{u} ) + \boldsymbol{\mu}^\top
\boldsymbol{u} \} = - \sup_{ (\boldsymbol{x}, \boldsymbol{u} ) \in
\mathbb{R}^{n+r} } \{ (-\boldsymbol{\mu})^\top \boldsymbol{u} -
F(\boldsymbol{x}, \boldsymbol{u} ) \} = - F^*(\boldsymbol{0} ,
-\boldsymbol{\mu}), \end{align*}
于是\begin{align*} q^* =
\sup_{\boldsymbol{\mu} \in \mathbb{R}^r} q(\boldsymbol{\mu}) =
\sup_{\boldsymbol{\mu} \in \mathbb{R}^r} \{ -F^*(\boldsymbol{0} ,
-\boldsymbol{\mu}) \} = - \inf_{\boldsymbol{\mu} \in \mathbb{R}^r}
F^*(\boldsymbol{0} , -\boldsymbol{\mu}) = - \inf_{\boldsymbol{\mu} \in
\mathbb{R}^r} F^*(\boldsymbol{0} , \boldsymbol{\mu}), \end{align*}
由此易知,若想强对偶成立,应有\begin{align*}
\inf_{\boldsymbol{x} \in \mathbb{R}^n} f(\boldsymbol{x}) = -
\inf_{\boldsymbol{\mu} \in \mathbb{R}^r} F^*(\boldsymbol{0} ,
\boldsymbol{\mu}). \end{align*}
三、含有不等式约束的优化
式(\ref{equ: general optimization duality
f}
)和式(\ref{equ: general optimization duality
p}
)中F
和p
的不同选择可以得到不同的对偶问题,考虑含有不等式约束的优化问题:\begin{align} \label{equ: optimization with
inequality constraints} \begin{split} \min_{\boldsymbol{x}} & \
f(\boldsymbol{x}) \\ \mbox{s.t.} & \ \boldsymbol{x} \in X, \
\boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{0}. \end{split}
\end{align}
其中X
是\mathbb{R}^n
的非空子集,f: X \mapsto \mathbb{R}
,g_j: X \mapsto \mathbb{R}
是给定函数。引入扰动约束集合\begin{align*}C_{\boldsymbol{u} } = \{
\boldsymbol{x} \in X \ | \ \boldsymbol{g}(\boldsymbol{x}) \leq
\boldsymbol{u} \}, \ \boldsymbol{u} \in \mathbb{R}^r.
\end{align*}
和函数\begin{align*} F(\boldsymbol{x},
\boldsymbol{u} ) = \begin{cases} f(\boldsymbol{x}) &
\boldsymbol{x} \in C_{\boldsymbol{u} }, \\ \infty & \boldsymbol{x}
\not \in C_{\boldsymbol{u} }. \end{cases} \end{align*}
显然对于\forall \boldsymbol{x} \in C_{
\boldsymbol{0} }
有F(\boldsymbol{x}, \boldsymbol{0} ) =
f(\boldsymbol{x})
且\begin{align*} p(\boldsymbol{u} ) =
\inf_{\boldsymbol{x} \in \mathbb{R}^n} F(\boldsymbol{x}, \boldsymbol{u} )
= \inf_{\boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq
\boldsymbol{u} } f(\boldsymbol{x}), \end{align*}
我们称之为原始函数,易知\begin{align*} w^* =
p(\boldsymbol{0} ) = \inf_{\boldsymbol{x} \in X,
\boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{0} } f(\boldsymbol{x}).
\end{align*}
另一方面,\begin{align} \label{equ: Lagrangian function}
q(\boldsymbol{\mu}) = \inf_{ \boldsymbol{u} \in \mathbb{R}^r }
\left\{ p(\boldsymbol{u} ) + \boldsymbol{\mu}^\top \boldsymbol{u}
\right\} = \inf_{\boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq
\boldsymbol{u} } \left\{ f(\boldsymbol{x}) + \boldsymbol{\mu}^\top
\boldsymbol{u} \right\} = \begin{cases} \inf_{\boldsymbol{x} \in X}
\left\{ f(\boldsymbol{x}) + \boldsymbol{\mu}^\top
\boldsymbol{g}(\boldsymbol{x}) \right\} & \boldsymbol{\mu} \geq
\boldsymbol{0}, \\ - \infty & otherwise. \end{cases}\end{align}
我们称之为对偶函数或Lagrangian函数。
例4.2.1[线性规划的对偶]:考虑如下形式的线性规划:\begin{align*} \min_{\boldsymbol{x}} & \
\boldsymbol{c}^\top \boldsymbol{x} \\ \mbox{s.t.} & \
\boldsymbol{a}_j^\top \boldsymbol{x} \geq b_j, j = 1, \dots, r.
\end{align*}
其中\boldsymbol{c} \in
\mathbb{R}^n
,\boldsymbol{a}_j \in
\mathbb{R}^n
,b_j \in \mathbb{R}
,j = 1, \dots, r
。于是由式(\ref{equ: Lagrangian
function}
)知对于\boldsymbol{\mu} \geq
\boldsymbol{0}
有\begin{align*} q(\boldsymbol{\mu}) =
\inf_{\boldsymbol{x} \in \mathbb{R}^n} \left\{ \boldsymbol{c}^\top
\boldsymbol{x} + \sum_{j=1}^r \mu_j (b_j - \boldsymbol{a}_j^\top
\boldsymbol{x}) \right\} = \begin{cases} \boldsymbol{\mu}^\top
\boldsymbol{b} & \sum_{j=1}^r \mu_j \boldsymbol{a}_j = \boldsymbol{c},
\\ -\infty & otherwise. \end{cases} \end{align*}
对于其它的\boldsymbol{\mu} \in
\mathbb{R}^n
有q(\boldsymbol{\mu}) = -\infty
,因此对偶问题为\begin{align*}
\max_{\boldsymbol{\mu}} & \ \boldsymbol{\mu}^\top \boldsymbol{b} \\
\mbox{s.t.} & \ \sum_{j=1}^r \mu_j \boldsymbol{a}_j = \boldsymbol{c},
\ \boldsymbol{\mu} \geq \boldsymbol{0}. \end{align*}
四、增广Lagrangian对偶
依然考虑问题(\ref{equ: optimization with inequality
constraints}
),和之前相同,引入函数\begin{align*}
F_c(\boldsymbol{x}, \boldsymbol{u} ) = \begin{cases} f(\boldsymbol{x}) +
\frac{c}{2} \| \boldsymbol{u} \|^2 & \boldsymbol{x} \in
C_{\boldsymbol{u} }, \\ \infty & \boldsymbol{x} \not \in
C_{\boldsymbol{u} }. \end{cases} \end{align*}
其中c
是一个正数。显然对于\forall \boldsymbol{x} \in C_{
\boldsymbol{0} }
有F(\boldsymbol{x}, \boldsymbol{0} ) =
f(\boldsymbol{x})
且\begin{align*} p_c(\boldsymbol{u} ) =
\inf_{\boldsymbol{x} \in \mathbb{R}^n} F_c(\boldsymbol{x}, \boldsymbol{u}
) = \inf_{\boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq
\boldsymbol{u} } \left\{ f(\boldsymbol{x}) + \frac{c}{2} \|
\boldsymbol{u} \|^2 \right\}, \end{align*}
易知\begin{align*} w^* = p_c(\boldsymbol{0} )
= \inf_{\boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq
\boldsymbol{0} } f(\boldsymbol{x}). \end{align*}
即最小公共点没有改变。
另一方面,对偶函数\begin{align*} q_c(\boldsymbol{\mu}) =
\inf_{ \boldsymbol{u} \in \mathbb{R}^r } \{ p_c(\boldsymbol{u} ) +
\boldsymbol{\mu}^\top \boldsymbol{u} \} = \inf_{\boldsymbol{x} \in
X, \boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{u} } \left\{
f(\boldsymbol{x}) + \boldsymbol{\mu}^\top \boldsymbol{u} +
\frac{c}{2} \| \boldsymbol{u} \|^2 \right\}, \end{align*}
对于固定的\boldsymbol{x} \in X
,上式的下确界可以通过优化\boldsymbol{u}
的每一维依次得到,对于第j
维,\begin{align*} \min_{u_j} & \ \mu_j
u_j + \frac{c}{2} u_j^2 \\ \mbox{s.t.} & \ g_j(\boldsymbol{x}) \leq
u_j. \end{align*}
易知最优解为\begin{align*} g_j^+(\boldsymbol{x},
\boldsymbol{\mu}, c) = \max \left\{ -\frac{\mu_j}{c}, g_j(\boldsymbol{x})
\right\}, \ j = 1, \dots, r, \end{align*}
故\begin{align} \label{equ: augmented
Lagrangian function} q_c(\boldsymbol{\mu}) = \inf_{\boldsymbol{x}
\in X} \left\{ f(\boldsymbol{x}) + \boldsymbol{\mu}^\top
g^+(\boldsymbol{x}, \boldsymbol{\mu}, c) + \frac{c}{2} \|
g^+(\boldsymbol{x}, \boldsymbol{\mu}, c) \|^2 \right\}, \end{align}
其中g^+(\boldsymbol{x}, \boldsymbol{\mu},
c)
的第j
维是g_j^+(\boldsymbol{x}, \boldsymbol{\mu},
c)
。
式(\ref{equ: augmented Lagrangian
function}
)称作增广Lagrangian函数,相较于式(\ref{equ: Lagrangian function}
),增广Lagrangian函数多引入了最后那个二次项,这使得它多了些优异的性质,例如它常常是实值函数(当f
和g_j
都是连续函数且X
是紧集时),有时甚至是可微的。
五、极大极小问题
设函数\phi: X \times Z \mapsto R
,其中X
和Z
分别是\mathbb{R}^n
和\mathbb{R}^m
的非空子集,则极大极小问题可以形式化为:\begin{align*}
\min_{\boldsymbol{x}} & \ \sup_{\boldsymbol{z} \in Z}
\phi(\boldsymbol{x}, \boldsymbol{z}) \\ \mbox{s.t.} & \ \boldsymbol{x}
\in X. \end{align*}
和\begin{align*} \max_{\boldsymbol{z}} &
\ \inf_{\boldsymbol{x} \in X} \phi(\boldsymbol{x}, \boldsymbol{z}) \\
\mbox{s.t.} & \ \boldsymbol{z} \in Z. \end{align*}
一个有趣的问题是在什么条件下有极大极小等式\begin{align*}
\sup_{\boldsymbol{z} \in Z} \inf_{\boldsymbol{x} \in X}
\phi(\boldsymbol{x}, \boldsymbol{z}) = \inf_{\boldsymbol{x} \in X}
\sup_{\boldsymbol{z} \in Z} \phi(\boldsymbol{x}, \boldsymbol{z}).
\end{align*}
成立,且相应的极值都能取到,这在零和博弈和对偶优化理论里都是很常见的问题。
引入函数p: \mathbb{R}^m \mapsto [-\infty,
\infty]
:\begin{align} \label{equ: minimax
perturbation function} p(\boldsymbol{u} ) = \inf_{\boldsymbol{x} \in X}
\sup_{\boldsymbol{z} \in Z} \{ \phi(\boldsymbol{x}, \boldsymbol{z}) -
\boldsymbol{u} ^\top \boldsymbol{z} \}, \end{align}
这里p(\boldsymbol{u} )
可以看成是一个扰动函数,线性项\boldsymbol{u} ^\top
\boldsymbol{z}
是扰动项,设M
是p
的上境图,那么\begin{align*} w^* = p(
\boldsymbol{0} ) = \inf_{\boldsymbol{x} \in X} \sup_{\boldsymbol{z} \in Z}
\phi(\boldsymbol{x}, \boldsymbol{z}).\end{align*}
下面研究q^*
,在此先引入函数闭凹包的概念。函数f: X
\mapsto [-\infty, \infty]
的闭凹包为\begin{align*} cl(conc(f)) = -
cl(conv(-f)). \end{align*}
结合命题1.3.13知\begin{align} \label{equ: concave
closure} \sup_{\boldsymbol{x} \in X} f(\boldsymbol{x}) = -
\inf_{\boldsymbol{x} \in X} -f(\boldsymbol{x}) = - \inf_{\boldsymbol{x}
\in \mathbb{R}^n} cl(conv(-f))(\boldsymbol{x}) = \sup_{\boldsymbol{x} \in
\mathbb{R}^n} - cl(conv(-f))(\boldsymbol{x}) = \sup_{\boldsymbol{x} \in
\mathbb{R}^n} cl(conc(f))(\boldsymbol{x}). \end{align}
命题4.2.2:设函数\phi: X \times Z \mapsto R
,其中X
和Z
分别是\mathbb{R}^n
和\mathbb{R}^m
的非空子集。若对于\forall \boldsymbol{x} \in
X
,-cl(conc(\phi))(\boldsymbol{x},
\cdot)
是正常函数,考虑之前的MCMC框架,设函数p
的定义如式(\ref{equ: minimax perturbation
function}
),M = epi(p)
,那么对偶函数为\begin{align*} q(\boldsymbol{\mu}) =
\inf_{\boldsymbol{x} \in X} cl(conc(\phi))(\boldsymbol{x},
\boldsymbol{\mu}). \end{align*}
证明:将p(\boldsymbol{u} )
重新写为\begin{align*} p(\boldsymbol{u} ) =
\inf_{\boldsymbol{x} \in X} p_{\boldsymbol{x}}(\boldsymbol{u} ),
\end{align*}
其中p_{\boldsymbol{x}}(\boldsymbol{u} ) =
\sup_{\boldsymbol{z} \in Z} \{ \phi(\boldsymbol{x}, \boldsymbol{z}) -
\boldsymbol{u} ^\top \boldsymbol{z} \}, \boldsymbol{x} \in X
。将\phi(\boldsymbol{x},
\boldsymbol{z})
看作\boldsymbol{z}
的函数,易知有\begin{align*} -
\phi^*(\boldsymbol{x}, \boldsymbol{z}) = \sup_{\boldsymbol{z} \in Z} \{
\boldsymbol{u} ^\top \boldsymbol{z} + \phi(\boldsymbol{x}, \boldsymbol{z})
\} = p_{\boldsymbol{x}}(-\boldsymbol{u} ), \end{align*}
即p_{\boldsymbol{x}}(-\cdot)
是- \phi(\boldsymbol{x}, \cdot)
的共轭函数,由共轭定理(4)知
\begin{align} \label{equ: minimax duality}
p_{\boldsymbol{x}}^*(-\cdot) = - \phi^{**}(\boldsymbol{x}, \cdot) =
cl(conv(-\phi)) (\boldsymbol{x}, \cdot) = - cl(conc(\phi))
(\boldsymbol{x}, \cdot), \end{align}
于是\begin{align*}
p_{\boldsymbol{x}}^*(-\boldsymbol{\mu}) = - cl(conc(\phi))
(\boldsymbol{x}, \boldsymbol{\mu}). \end{align*}
因此对于任意\boldsymbol{\mu} \in
\mathbb{R}^m
有\begin{align*} q(\boldsymbol{\mu}) & =
\inf_{\boldsymbol{u} \in \mathbb{R}^m} \{ p(\boldsymbol{u} ) +
\boldsymbol{u} ^\top \boldsymbol{\mu} \} \\ & =
\inf_{\boldsymbol{u} \in \mathbb{R}^m}\inf_{\boldsymbol{x} \in X} \{
p_{\boldsymbol{x}}(\boldsymbol{u} ) + \boldsymbol{u} ^\top
\boldsymbol{\mu} \} \\ & = \inf_{\boldsymbol{x} \in X}
\inf_{\boldsymbol{u} \in \mathbb{R}^m} \{
p_{\boldsymbol{x}}(\boldsymbol{u} ) + \boldsymbol{u} ^\top
\boldsymbol{\mu} \} \\ & = \inf_{\boldsymbol{x} \in X} \left\{ -
\sup_{\boldsymbol{u} \in \mathbb{R}^m} \{ \boldsymbol{u} ^\top
(-\boldsymbol{\mu}) - p_{\boldsymbol{x}}(\boldsymbol{u} )\} \right \} \\
& = \inf_{\boldsymbol{x} \in X} \{
-p_{\boldsymbol{x}}^*(-\boldsymbol{\mu}) \} \\ & =
\inf_{\boldsymbol{x} \in X} cl(conc(\phi)) (\boldsymbol{x},
\boldsymbol{\mu}). \end{align*}
-cl(conc(\phi))(\boldsymbol{x}, \cdot)
是正常函数的条件是必需的,否则式(\ref{equ: minimax
duality}
)中的第二个等号可能不成立。此外我们还可得到如下一些结论:
- 一般来说,我们有\begin{align*} \sup_{\boldsymbol{z} \in Z}
\inf_{\boldsymbol{x} \in X} \phi(\boldsymbol{x}, \boldsymbol{z}) \leq
q^* \leq w^* = \inf_{\boldsymbol{x} \in X} \sup_{\boldsymbol{z} \in Z}
\phi(\boldsymbol{x}, \boldsymbol{z}), \end{align*}
其中第一个不等号成立是因为\begin{align*}
q(\boldsymbol{\mu}) = \inf_{\boldsymbol{u} \in \mathbb{R}^m} \{
p(\boldsymbol{u} ) + \boldsymbol{u} ^\top \boldsymbol{\mu} \} =
\inf_{\boldsymbol{u} \in \mathbb{R}^m} \inf_{\boldsymbol{x} \in X}
\sup_{\boldsymbol{z} \in Z} \{ \phi(\boldsymbol{x}, \boldsymbol{z}) +
\boldsymbol{u} ^\top(\boldsymbol{\mu} - \boldsymbol{z}) \} \geq
\inf_{\boldsymbol{u} \in \mathbb{R}^m} \inf_{\boldsymbol{x} \in X}
\phi(\boldsymbol{x}, \boldsymbol{\mu}) = \inf_{\boldsymbol{x} \in X}
\phi(\boldsymbol{x}, \boldsymbol{\mu}), \end{align*}
于是有\begin{align*} q^* =
\sup_{\boldsymbol{\mu} \in \mathbb{R}^m} q(\boldsymbol{\mu}) \geq
\sup_{\boldsymbol{\mu} \in \mathbb{R}^m} \inf_{\boldsymbol{x} \in X}
\phi(\boldsymbol{x}, \boldsymbol{\mu}) \geq \sup_{\boldsymbol{z} \in Z}
\inf_{\boldsymbol{x} \in X} \phi(\boldsymbol{x}, \boldsymbol{z}).
\end{align*}
第二个等号是弱对偶定理,由此可见,若极大极小等式成立,则有强对偶成立。
- 若\begin{align*} \phi(\boldsymbol{x},
\boldsymbol{z}) = cl(conc(\phi)) (\boldsymbol{x}, \boldsymbol{z}),
\forall \boldsymbol{x} \in X, \boldsymbol{z} \in Z \end{align*}
成立且对于\forall \boldsymbol{x} \in
X
,-cl(conc(\phi)) (\boldsymbol{x},
\cdot)
是正常函数,则有\begin{align*} q^* =
\sup_{\boldsymbol{z} \in \mathbb{R}^m} q(\boldsymbol{z}) =
\sup_{\boldsymbol{z} \in \mathbb{R}^m} \inf_{\boldsymbol{x} \in X}
cl(conc(\phi))(\boldsymbol{x}, \boldsymbol{z}) = \sup_{\boldsymbol{z}
\in Z} \inf_{\boldsymbol{x} \in X} \phi(\boldsymbol{x}, \boldsymbol{z}),
\end{align*}
这意味着若\phi = cl(conc(\phi))
,则极大极小等式等价于强对偶关系。
- 由式(\ref{equ: concave closure}
)知\sup_{\boldsymbol{z} \in Z}
\phi(\boldsymbol{x}, \boldsymbol{z}) = \sup_{\boldsymbol{z} \in
\mathbb{R}^m} cl(conc(\phi)) (\boldsymbol{x},
\boldsymbol{z})
,于是\begin{align*} w^* =
\inf_{\boldsymbol{x} \in X} \sup_{\boldsymbol{z} \in Z}
\phi(\boldsymbol{x}, \boldsymbol{z}) = \inf_{\boldsymbol{x} \in X}
\sup_{\boldsymbol{z} \in \mathbb{R}^m} cl(conc(\phi)) (\boldsymbol{x},
\boldsymbol{z}). \end{align*}
若对于\forall \boldsymbol{x} \in
X
,-cl(conc(\phi)) (\boldsymbol{x},
\cdot)
是正常函数,由命题4.2.2知\begin{align*} q^* =
\sup_{\boldsymbol{z} \in \mathbb{R}^m} q(\boldsymbol{z}) =
\sup_{\boldsymbol{z} \in \mathbb{R}^m} \inf_{\boldsymbol{x} \in X}
cl(conc(\phi)) (\boldsymbol{x}, \boldsymbol{z}) \end{align*}
由此可知w^*
和q^*
分别是cl(conc(\phi))
的\inf \sup
值和\sup \inf
值。
一些例子,布布扣,bubuko.com
一些例子
标签:style blog class c ext color
原文地址:http://www.cnblogs.com/murongxixi/p/3730357.html
 设M
设Mn
?[?∞,∞]