标签：jpg   ace   display   name   log   namespace   ack   n+1   一点   

写在前面

今天的这场比赛。。。是可写的

还是我太菜了

T1走步(travel)

链接

Idea

这是一道数学题

前置芝士：余弦定理

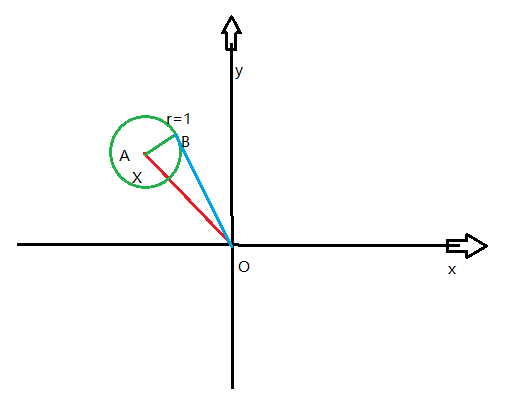
如图，点\(\mathcal A\)是走了\(n\)步所到达的点，到原点距离为\(x\)。（红线）

接下来走一步走到点\(\mathcal B\)（\(\mathcal B\)为\(\odot A\)上一点且\(r_A=1\),），设其到原点距离\(\mathcal {BO}=y\)，（蓝线）

在$ \bigtriangleup OAB$中，使用余弦定理，得：
\[ y^2=x^2+1-2x \cos \theta \]
我们发现\(\cos \theta\)的期望为零。。。（这一点希望读者自己思考

所以，式子化简成
\[ y^2=x^2+1 \]
因为我们求的正是\(E(\mathcal D^2)\)，我们上面提到，\(\mathcal A\)是第\(n\)步走到的点，\(\mathcal B\)是第\(n+1\)步走到的点，那么\(f_{n+1}^2=f_n^2+1,n \ge 1\)，所以第\(n\)步时,\(E(\mathcal D^2)=n\)。

所以，输出\(n\)即可。

另注：本题只有一个测试点

Code

namespace Sol{
    inline int Main(){
        put(read());//不解释，嘻嘻
        return 0;
    }
}

T2遥不可及

链接

Idea

对于本题，分块、莫队都可以写。代码等我回来再贴

这里说一种不严格的\(\mathcal O(n^2 \log n)\)。

因为使用了二分，还加了些剪枝，于是卡过了数据。具体可以看代码。

Code

namespace Sol{
    vector<int>v[maxn];
    int n,m,T,ans;
    int a[maxn];
    inline int Main(){
        n=read(); m=read(); T=read();
        for(int i=1;i<=n;i++){
            a[i]=read();
            v[a[i]].push_back(i);
        }
        while(T--){
            ans=0;
            int l=read(),r=read(),x;
            if(l==r){puts("0");continue;}
            for(int i=l;i<=r;i++){
                if(r-i<=ans)break;//如果r-i比我当前搜到的答案短，那肯定找不到了。continue
                if(v[x=a[i]].size()<2) continue;//如果找不到当前数字相等的点。continue
                if(v[x][v[x].size()-1]-i<=ans) continue; //
                //就是这三个剪枝，
                int xx=lower_bound(v[x].begin(),v[x].end()-1, r)-v[x].begin();
                if(v[x][xx]>r) xx-=1;//以上两行请自己理解/喷脸
                ans=max(ans,v[x][xx]-i);//更新答案
            }
            printf("%d\n",ans);
        }
        return 0;
    }
}
//不知为什么，这题我用cin,cout竟然只有10 pts/jk

T3颠倒黑白

链接

Idea

目前只知道std是爆搜？\喷脸

Code

//容我回来再补

\[ \mathcal The \quad End \]

\[ \text{我仍然在无人问津的阴雨霉湿之地;和着雨音唱着没有听众的歌曲-《世末歌者》} \]

1108 模拟赛

标签：jpg   ace   display   name   log   namespace   ack   n+1   一点   

原文地址：https://www.cnblogs.com/cbyyc/p/11822961.html