标签:线段 问题 info 代表作 ali 一个 span 选项 关于
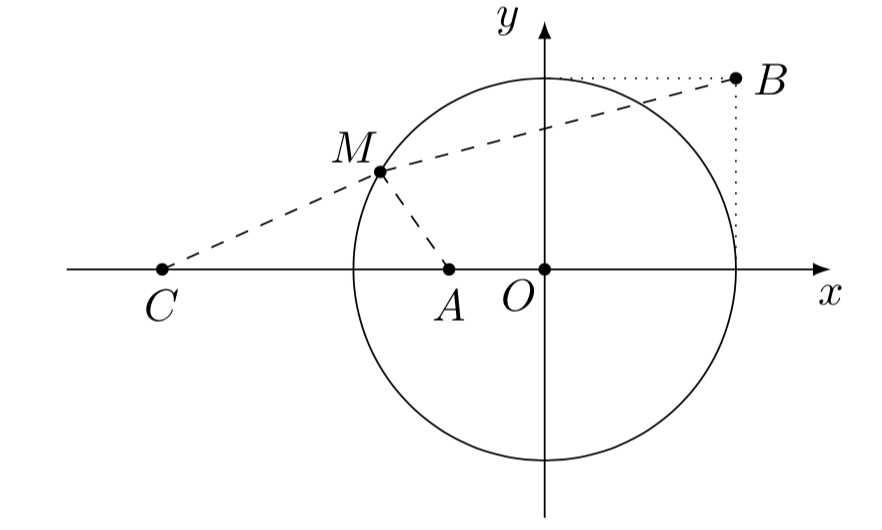
阿波罗尼斯是古希腊著名数学家,与欧几里得,阿基米德被成为亚历山大时期的数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线论》一书,阿波罗尼斯圆是他的研究成果之一,指的是\(:\)已知动点\(M\)与两定点\(A,B\)距离之比为\(\lambda\) \((\lambda>0\),\(\lambda\neq 1)\),那么点\(M\)的轨迹就是阿波罗尼斯圆.如动点\(M\)与两定点 $ A\left(\dfrac{9}{5},0\right)$ ,\(B(5,0)\)的距离之比为 \(\dfrac35\) 时的阿波罗尼斯圆为\(x^2+y^2=9\).下面,我们来研究与此相关的一个问题.已知圆\(O:x^2+y^2=1\)上的动点\(M\)和定点\(A\left(-\dfrac{1}{2},0\right)\), \(B(1,1)\) 则 \(2|MA|+|MB|\) 的最小值为\((\qquad)\)
\(\mathrm{A}.\sqrt{6}\) \(\qquad\mathrm{B}.\sqrt{7}\) \(\qquad\mathrm{C}.\sqrt{10}\) \(\qquad\mathrm{D}.\sqrt{11}\)
解析:
记点\(C(-2,0)\),则\(C,A\)两点是关于圆\(O\)的对反演点,
标签:线段 问题 info 代表作 ali 一个 span 选项 关于
原文地址:https://www.cnblogs.com/Math521/p/11827307.html