标签:click cstring 有一个 处理 targe code 部分 个数 重复
这道题很久之前就想做了,但是还是拖到了现在;
看这道题的时候还是很懵,看了题解(话说这题解写的贼好)恍然大悟;
路径条数太多,一个个遍历会T,我们需要换一个思路,遍历观察员,这样就是O(n)的;
我们可以想,哪些点能对当前观察员做出贡献;
观察员在p点的w[p]时间观察,有一个等式dep[p]+w[p]=dep[s[i]],s[i]是一个起点,
满足这个等式的路径就会对观察点做出贡献;
然而这只是上行路;
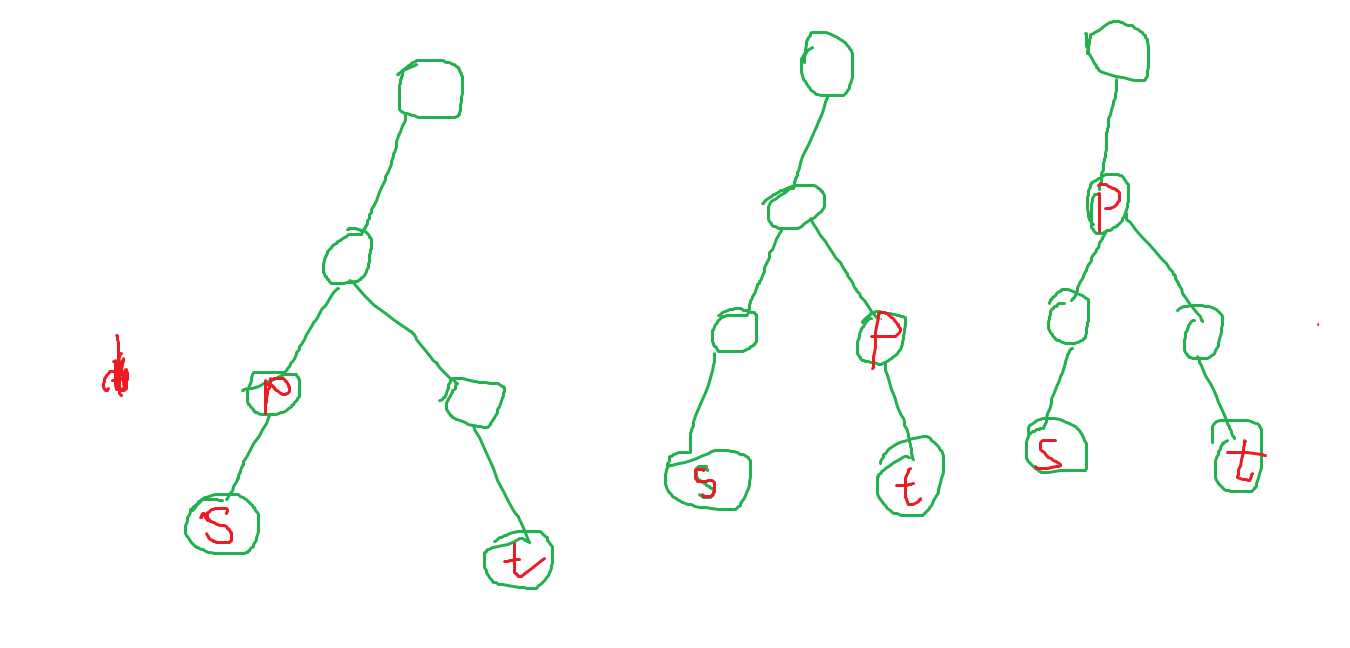
如果p在一条路径的下行路,设dis[i]=dep[s[i]]+dep[t[i]]-2*dep[lca],那么dis[i]-w[p]=dep[t[i]]-dep[p];
那么满足dis[i]-dep[p]=w[p]-dep[t[i]]的会对答案做出贡献;
我们设两个桶,分别装着上行路的贡献和下行路的贡献;
遍历到当前点时,就可以直接根据等式得出自己的答案;
由于lca的位置比较特殊,上行路下行路会算两遍,所以提前预处理减掉多余的部分;
我们可以知道,面对当前节点什么节点会对自己做出贡献,就是起点或终点在自己的子树上;
所以一旦离开了自己的子树,我们需要把已经没有用的路径做出的贡献从桶中减去,(毕竟桶里的是标量数值,并没有什么状态);
p在上行路上的贡献不能减去,因为这条路径还能往上做出贡献,在下行路也是如此;
只有当前节点是这条路径的lca时,这条路径的贡献才算算完;
所以在遍历当前点后,将所有路径的lca是自己的减去贡献即可;
整理一下,
上行路公式dep[p]+w[p]=dep[s[i]],所以记录上行路时,将遍历的点作为一个路径起点加上贡献 b1[js[x]]++;
每次从b1[dep[x]+w[p]]取出当前值;
下行路公式dis[i]-dep[t[i]]=w[p]-dep[p],遍历每个点时将b2[dis[i]-dep[t[i]]]++,找出所有以他为终点的路径,
每次从b2[w[x]-dep[x]]里面取出当前值;
然而取出来的值并不是这个点所观察的数量,前后的差值才是;
因为只有子树上的路径才对当前点做出贡献,所以,在遍历一个点时,先将桶里的值记录下来,再将子树上的贡献加入桶中,
当然在当前节点的子树里的不经过当前点的路径在遍历的时候已经减去了贡献;
最后计算差值即为当前点的答案;
代码不长,其实真的懂了也不过如此吧;
2019RP++

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int maxn=3e6+10; 6 7 struct node 8 { 9 int pre[maxn*2],last[maxn],other[maxn*2],l=0; 10 void add(int x,int y) 11 { 12 l++; 13 pre[l]=last[x]; 14 last[x]=l; 15 other[l]=y; 16 } 17 }mp,a1,a2; 18 //建图,mp为原图,a1是以当前点为终点的路径,a2是以当前点为lca的路径 19 20 int n,m,w[maxn]; 21 22 int s[maxn],t[maxn],js[maxn];//js是以当前点为起点的个数 23 int dep[maxn],jump[maxn][30],dis[maxn]; 24 //——————————————————————————LCA 25 void dfs(int x,int fa) 26 { 27 jump[x][0]=fa; 28 dep[x]=dep[fa]+1; 29 for(int p=mp.last[x];p;p=mp.pre[p]) 30 { 31 int v=mp.other[p]; 32 if(v==fa) continue; 33 dfs(v,x); 34 } 35 } 36 37 void pre_pare() 38 { 39 for(int j=1;j<=20;j++) 40 { 41 for(int i=1;i<=n;i++) 42 { 43 jump[i][j]=jump[jump[i][j-1]][j-1]; 44 } 45 } 46 } 47 48 int LCA(int x,int y) 49 { 50 if(dep[x]<dep[y]) swap(x,y); 51 for(int j=0;j<=20;j++) 52 { 53 if((dep[x]-dep[y])&(1<<j)) x=jump[x][j]; 54 } 55 if(x==y) return x; 56 for(int j=20;j>=0;j--) 57 { 58 if(jump[x][j]!=jump[y][j]) 59 { 60 x=jump[x][j]; 61 y=jump[y][j]; 62 } 63 } 64 return jump[x][0]; 65 } 66 //______________________________________LCA 67 int b1[maxn],b2[maxn*2];//b1上行路,b2下行路 68 int ans[maxn];//记录答案 69 70 void dfs2(int x) 71 { 72 int t1=b1[dep[x]+w[x]],t2=b2[w[x]-dep[x]+maxn];//数组下标不能为负数 73 for(int p=mp.last[x];p;p=mp.pre[p]) 74 { 75 int v=mp.other[p]; 76 if(v==jump[x][0]) continue; 77 dfs2(v); 78 } 79 b1[dep[x]]+=js[x]; 80 for(int p=a1.last[x];p;p=a1.pre[p]) 81 { 82 int v=a1.other[p]; 83 b2[dis[v]-dep[t[v]]+maxn]++; 84 } 85 ans[x]+=b1[dep[x]+w[x]]-t1+b2[w[x]-dep[x]+maxn]-t2; 86 for(int p=a2.last[x];p;p=a2.pre[p]) 87 { 88 int v=a2.other[p]; 89 b1[dep[s[v]]]--; 90 b2[dis[v]-dep[t[v]]+maxn]--; 91 } 92 } 93 94 int main() 95 { 96 scanf("%d%d",&n,&m); 97 for(int i=1;i<n;i++) 98 { 99 int x,y; 100 scanf("%d%d",&x,&y); 101 mp.add(x,y); 102 mp.add(y,x); 103 } 104 dfs(1,0); 105 pre_pare(); 106 for(int i=1;i<=n;i++) scanf("%d",&w[i]); 107 for(int i=1;i<=m;i++) 108 { 109 scanf("%d%d",&s[i],&t[i]); 110 int lca=LCA(s[i],t[i]); 111 js[s[i]]++; 112 dis[i]=dep[s[i]]+dep[t[i]]-2*dep[lca];//记录路径的长度 113 a1.add(t[i],i);//方便找到当前终点所在的路径 114 a2.add(lca,i);//当前lca所在的路径 115 if(w[lca]+dep[lca]==dep[s[i]]) ans[lca]--;//上面会加两次,减去重复的 116 } 117 118 dfs2(1); 119 120 for(int i=1;i<=n;i++) 121 { 122 printf("%d ",ans[i]); 123 } 124 return 0; 125 }
标签:click cstring 有一个 处理 targe code 部分 个数 重复
原文地址:https://www.cnblogs.com/WHFF521/p/11832703.html