标签:比较 测试数据 www computer 因此 不同 下一步 测试 问题
决策树分类是数据挖掘中分类分析的一种算法。顾名思义,决策树是基于“树”结构来进行决策的,是人类在面临决策问题时一种很自然的处理机制。例如下图一个简单的判别买不买电脑的决策树:
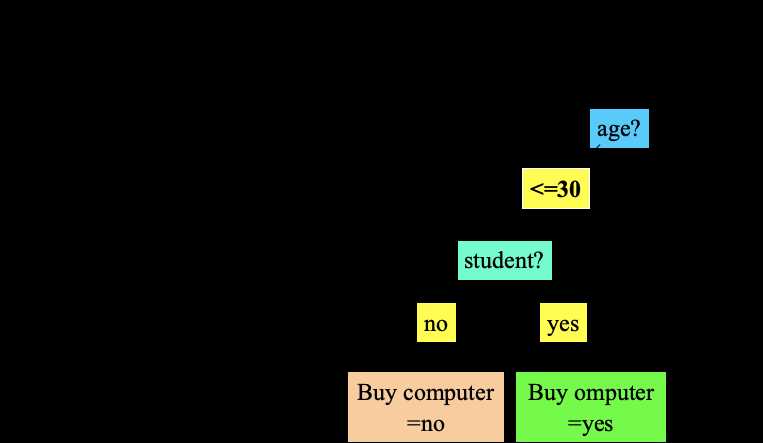



下图是一个测试数据集,我们以此数据集为例,来看下如何生成一棵决策树。
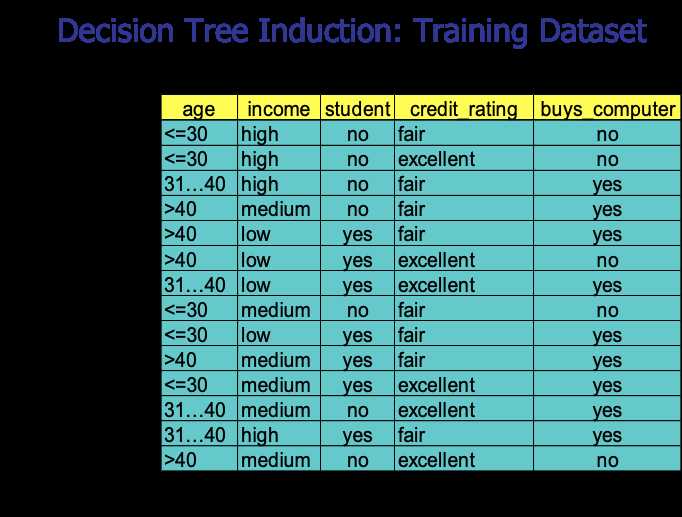
决策树分类的主要任务是要确定各个类别的决策区域,或者说,确定不同类别之间的边界。在决策树分类模型中,不同类别之间的边界通过一个树状结构来表示。
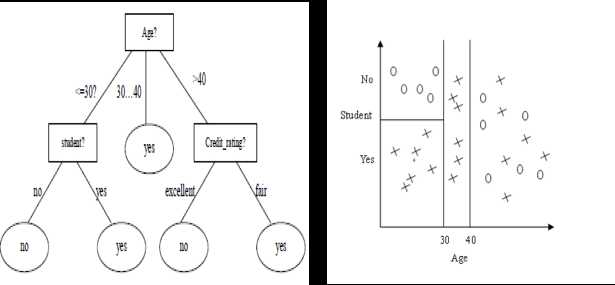
通过以上分析,我们可以得出以下几点:
因此,决策树建树算法就是:选择树根的过程


第一步,选择属性作为树根
比较流行的属性选择方法:信息增益
信息增益最大的属性被认为是最好的树根
在选择属性之前,我们先来了解一个概念:熵 什么是熵?什么是信息?如何度量他们?
下面这个文章通俗易懂的解释了这个概念
http://www.360doc.com/content/19/0610/07/39482793_841453815.shtml
熵用来表示不确定性的大小
信息用来消除不确定性
实际上,给定训练集S,信息增益代表的是在不考虑任何输入变量的情况下确定S中任一样本所属类别需要的信息(以消除不确定性)与考虑了某一输入变量X后确定S中任一样本所属类别需要的信息之间的差。差越大,说明引入输入变量X后,消除的不确定性,该变量对分类所起的作用就越大,因此被称为是好的分裂变量。换句话说,要确定S中任一样本所属类别,我们希望所需要的信息越少越好,而引入输入变量X能够减少分类所需要的信息,因此说输入变量X为分类这个数据挖掘任务带来了信息增益。信息增益越大,说明输入变量X越重要,因此应该被认为是好的分裂变量而优先选择。
因此,计算信息增益的总的思路是:
1) 首先计算不考虑任何输入变量的情况下要确定S中任一样本所属类别需要的熵Entropy(S);
2) 计算引入每个输入变量X后要确定S中任一样本所属类别需要的熵Entropy (X,S);
3) 计算二者的差,Entropy (S) - Entropy (X, S),此即为变量X所能带来的信息(增益),记为Gain(X,S)。
结合上面对于熵的解释的文章里,我们能得出求熵的公式:
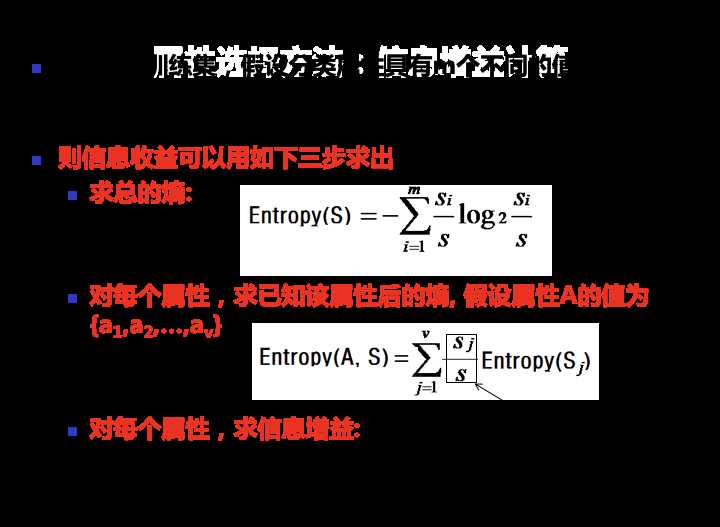
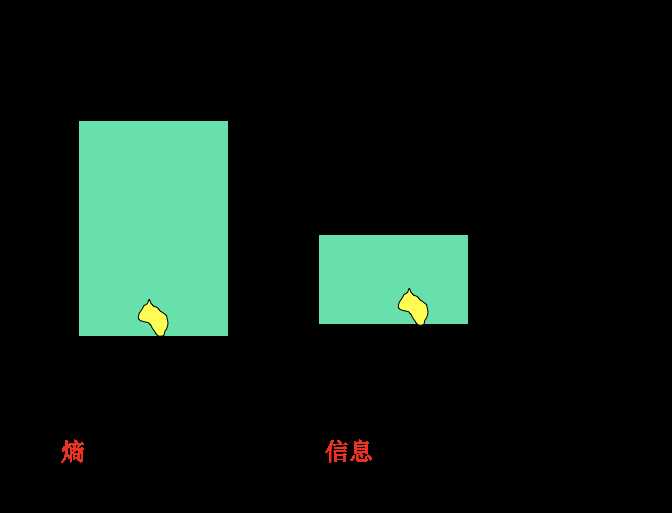
下图很形象的解释了熵代表的含义。
我们还以上面的一组数据来分析,信息增益具体应该怎么算
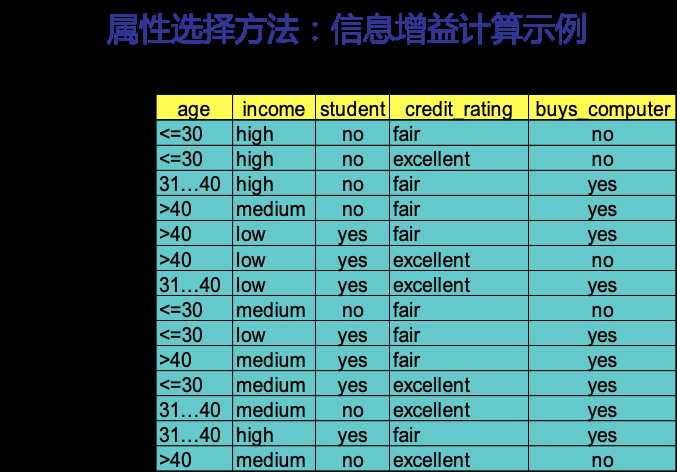
根据上面的讨论,我们先用公式计算不考虑任何输入属性时,要确定训练集S中任一样本所属类别需要的熵。
此例子中,目标属性即buys_computer,有2个不同的取值,yes和no,因此有2个不同的类别(m=2)。设P对应buys_computer=yes的情况,N对应buys_computer=no的情况,则P有9个样本,N有5个样本。所以,总的熵就是:
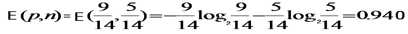
即,E(p,n) = E(9,5) = 0.940
然后我们来求属性age的熵,age有三个属性,样本个数分别为5,4,5,所以属性age的熵就是:
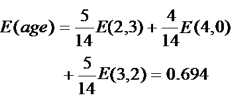
最后,我们可以求出属性age的信息增益为:
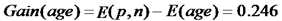
同样的,我们可以分别求出income,student和credit_rating的信息增益

finally,我们可以得出属性age的信息增益最大,所以,应该用属性age作为树根。
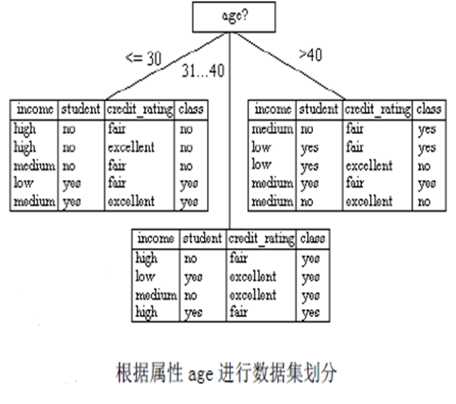
确定好树根之后,下一步我们还要按照刚才的步骤来确定下一个节点的左右子树分别用哪个属性作为树根,直到最后得出完整的决策树。
虽然决策树分类算法可以快速的预测分类,但是也会有过度拟合(Overfitting)的问题。
有些生成的决策树完全服从于训练集,太循规蹈矩,以至于生成了太多的分支,某些分支可能是一些特殊情况,出现的次数很少,不具有代表性,更有甚者仅在训练集中出现,导致模型的准确性很低。
通常采用剪枝的方式来克服 overfitting,剪枝有两种方法:
先剪:构造树的过程中进行修剪。不符合条件的分支则不建。
后剪: 整个树生成之后进行修剪

标签:比较 测试数据 www computer 因此 不同 下一步 测试 问题
原文地址:https://www.cnblogs.com/hupc/p/11831307.html