标签:影响 参数 image 最好 计算 图片 函数 直线 alt
最小二乘法可以更广泛地应用于非线性方程中,我们可以使用一些已知的离散的点,拟合出一条与这些离散点最为接近的曲线,从而可以分析出这些离散点的走向趋势。
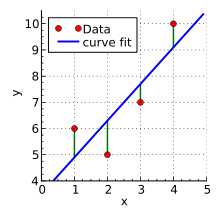
设x和y之间的函数关系由直线方程:
y=ax+b
公式中有两个待定参数,b代表截距,a代表斜率。问题在于,如何找到“最合适”的a和b使得尽可能多的数据落在或者更加靠近这条拟合出来的直线上;
我们关心的是方程中的a和b,也就是说,在这个待定的方程中,a和b才是所求的变量,它们可以描述出x和y的关系。 所以我们接下来的任务就是找到一组最好的a和b。
我们对a和b的要求就是,使得所有x和y相对拟合直线的误差总和最小。也就是说,我们要考虑的是,要使这些数据点距离拟合直线的和最小,距离最短,这样就可以使得尽可能多的数据成为有效点。
一.是我们要将误差最小化
二.是我们将误差最小化的方法是使误差的平方和最小化。(用误差平方和最小化来约束误差的原因是要规避负数对计算的影响)



标签:影响 参数 image 最好 计算 图片 函数 直线 alt
原文地址:https://www.cnblogs.com/-wenli/p/11846285.html