[JZOJ6345]:ZYB建围墙（数学+构造）

标签：--   不可   思考   name   交流   直接   bit   san   算法   

题目描述

　　$ZYB$之国是特殊的六边形构造。

　　已知王国一共有$N$户家庭，每个家庭需占据一个不同的六边形格子。
　　王国里交流很频繁，所以这些家庭要构成一个连通区域；同时出于安全考虑，国王$ZYB$想在外面“围”一圈墙。
　　围墙需要遵守这样的规则：
　　$1.$墙也是建在格子上的。
　　$2.$墙不能建在任何一户家庭占据的格子上。
　　$3.$任何一户家庭都不可能走到围墙外面去。
　　$4.$围墙不一定要“贴”着家庭建，可以多围一些格子。
　　定义围墙的长度为它占据的格子的数量。
　　请你帮国王$ZYB$安排每户家庭的具体位置以及围墙的建造方案，使得围墙的长度最短。

输入格式

　　从文件$wall.in$中读入数据。
　　只读入一个数，表示家庭的数量$N$。

输出格式

　　输出到文件$wall.out$中。
　　输出一个数表示围墙的最小长度。

样例

样例输入1：

6

样例输出1：

12

样例输入2：

9

样例输出2：

14

数据范围与提示

　　前$20\%$：$N\leqslant 10$。
　　前$40\%$：$N\leqslant 20$。
　　前$70\%$：$N\leqslant 1,000$。
　　另有$10\%$：$N=6\times \frac{K(K+1)}{2}+1(K\in\mathbb{N})$
　　$100\%$：$1\leqslant N\leqslant 10^9$

题解

转化一下思想，先选择家庭的位置，然后再围轮廓。

显然家庭越集中越好。

先从另$10\%$的算法入手，只需要将其围成如下图这样即可$\downarrow$

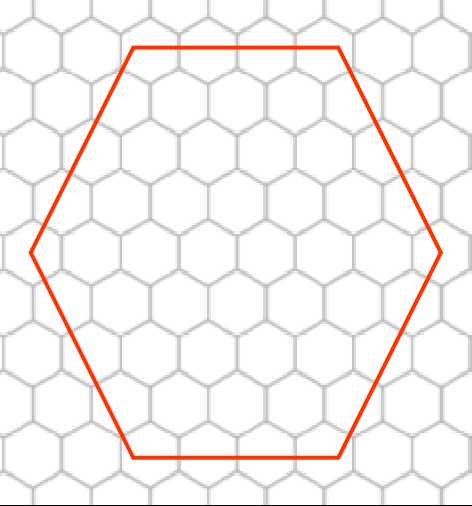
答案显而易见，就是边长$-1$再乘$6$。

在来考虑一般情况，可以先围城这样，然后思考如何接着往里填。

首先，要知道下图中两种情况代价是一样的$\downarrow$

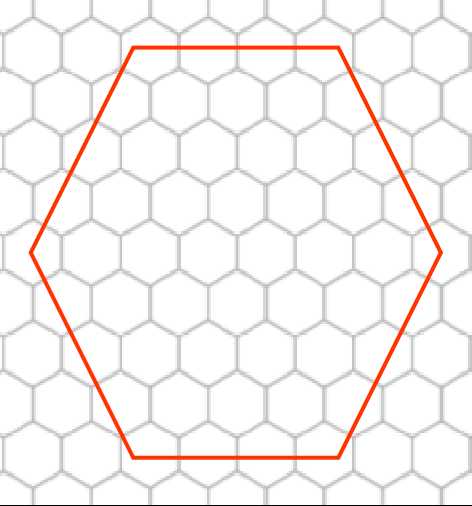
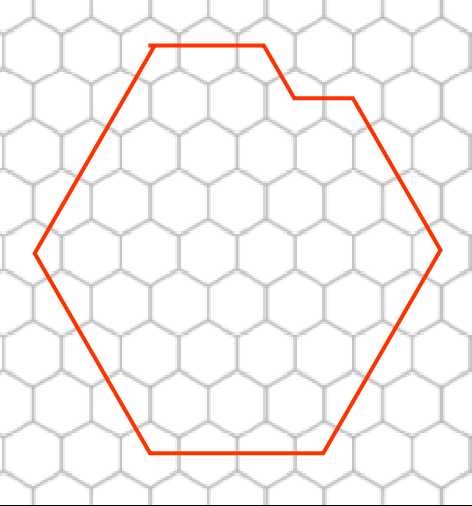
所以，遇到这种情况，不如直接将其填满。

接着考虑问题，也就是考虑先将$n$个家庭建成了正六边形后剩下的该怎么建。

假设多出来了一个，那么显然如下图中这么建更优$\downarrow$

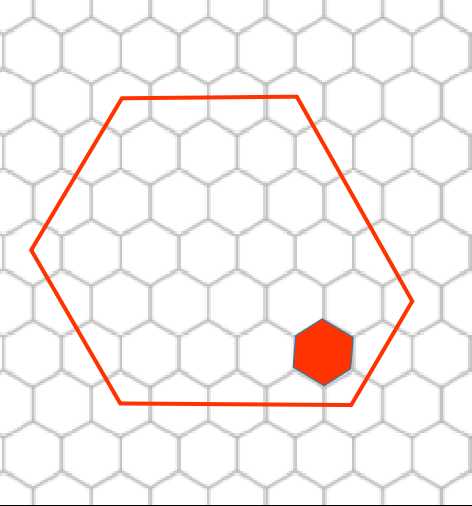
这样多花的代价为$1$，而这样的点可以建原六边形边长$-1$个。

现在假设我们把这原六边形边长$-1$个位置填满了。

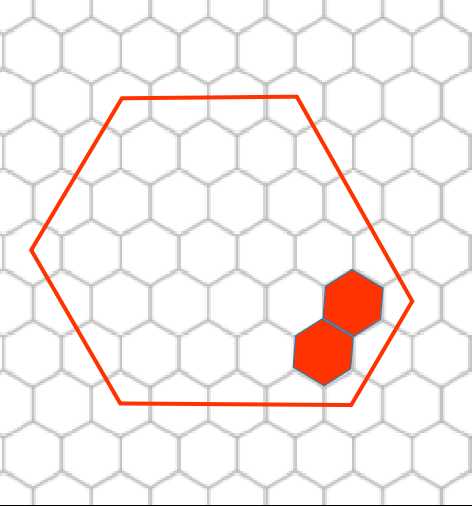
考虑接下来怎么填。

接着再扩一条边，扩的这条边显然与上一次扩的边相邻不劣，因为这样我们将获得原六边形边长个位置。

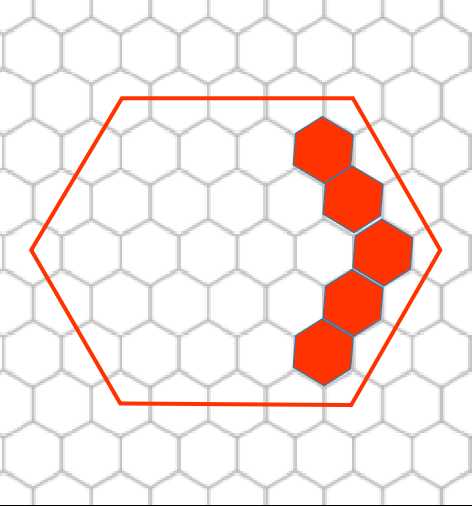
一直这么填就好了。

时间复杂度：$\Theta(\sqrt{N})$。

期望得分：$100$分。

实际得分：$100$分。

代码时刻

#include<bits/stdc++.h>
using namespace std;
int N;
int ans;
int main()
{
	scanf("%d",&N);N--;
	int now=0,fla=1;
	for(int i=1;i<=N;i++)
	{
		if(now+(i-1)*6>N)
		{fla=i-1;break;}
		now+=(i-1)*6;
	}
	ans=6*fla;N-=now;
	if(!N){printf("%lld",ans);return 0;}
	ans++;N-=fla-1;
	while(N>0){N-=fla;ans++;}
	printf("%lld",ans);
	return 0;
}

rp++

[JZOJ6345]:ZYB建围墙（数学+构造）

标签：--   不可   思考   name   交流   直接   bit   san   算法   

原文地址：https://www.cnblogs.com/wzc521/p/11848792.html