标签:数论 mat 树节点 如何 运算 一段 逆序对 键值 优化
| Floyd | Bellman-Ford | Dijkstra |
|---|---|---|
| 每对结点之间的最短路 | 单源最短路 | 单源最短路 |
| 无负环的图 | 任意图 | 非负权图 |
| \(O(N^3)\) | \(O ( NM )\) | \(O((N+M)log\ M)\) |
priority_queue<pii>q;
void dijkstra(int S){
memset(dis,inf,sizeof(dis)),memset(vis,0,sizeof(vis));
q.push(make_pair(dis[S]=0,S));
while(!q.empty()){
int u=q.top().second;q.pop();
if(vis[u]) continue;vis[u]=1;
for(int i=head[u],v;i;i=e[i].nxt)
if(dis[v=e[i].v]>dis[u]+e[i].w) q.push(make_pair(-(dis[v]=dis[u]+e[i].w),v));
}
}struct重载:
struct node{
int dis,pos;
node():dis(0),pos(0){}//无参数初始化
node(int a,int b):dis(a),pos(b){}//带参初始化
bool operator <(const node &x)const{return x.dis<dis;}//从小到大
}queue<int>q;
int dis[N],len[N];bool vis[N];
bool spfa(int s){
for(int i=1;i<=n;++i) dis[i]=inf,vis[i]=0,len[i]=-1;
while(!q.empty()) q.pop();
dis[s]=len[s]=0,q.push(s),vis[s]=1;
while(!q.empty()){
int u=q.front();q.pop(),vis[u]=0;
if(len[u]>=n) return 1;
for(int i=head[u],v;i;i=e[i].nxt)
if(dis[v=e[i].v]>dis[u]+e[i].w)
dis[v]=dis[u]+e[i].w,len[v]=len[u]+1,(!vis[v])?(vis[v]=1,q.push(v),1):1;
}
return 0;
}\(f[i][j]\):从\(i\)号顶点到\(j\)号顶点只经过前\(k\)号点的最短路程
\(k\)是阶段 所以必须位于最外层 而\(i和j\)为附加状态
for (k=1;k<=n;k++)
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
f[i][j] = min(f[i][j],f[i][k]+f[k][j]);给一个正权无向图,找一个最小权值和的环
这一定是一个简单环 考虑环上编号最大的结点\(u\)
\(f[u-1][x][y]\)和\((u,x), (u,y)\)共同构成了环。
在 Floyd 的过程中枚举\(u\),计算这个和的最小值即可
有向图的最小环问题 可枚举起点\(s=1\sim n\) 执行对优化的\(Dijsktra\)求解单源最短路径\(s\)一定为第一个被从堆中取出节点 扫描\(s\)所有出边 扩展、更新完成后 令\(d[s]=+\infty\) 然后继续求解 当s第二次被从堆中取出时 \(d[s]\)就是经过点\(s\)的最小环长度
找最小环 并输出一个最小环方案
int n,m,mp[N][N],dis[N][N],pos[N][N];
vector<int>path;
void get_path(int x,int y){
if(!pos[x][y]) return;
get_path(x,pos[x][y]);
path.push_back(pos[x][y]);
get_path(pos[x][y],y);
}
int main(){
scanf("%d%d",&n,&m);
int ans=inf;
memset(mp,inf,sizeof(mp));
for(int i=1;i<=n;++i) mp[i][i]=0;
for(int i=1,x,y,w;i<=m;++i)
scanf("%d%d%d",&x,&y,&w),mp[x][y]=mp[y][x]=w;
memcpy(dis,mp,sizeof(mp));
for(int k=1;k<=n;++k){
for(int i=1;i<k;++i)
for(int j=i+1;j<k;++j)
if((long long)dis[i][j]+mp[i][k]+mp[k][j]<ans){
ans=dis[i][j]+mp[i][k]+mp[k][j];
path.clear(),path.push_back(i);
get_path(i,j);path.push_back(j),path.push_back(k);
}
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j],pos[i][j]=k;
}
if(ans==inf) return puts("No solution."),0;
for(int i=0;i<path.size();++i) printf("%d ",path[i]);
return 0;
}已知一个有向图中任意两点之间是否有连边,要求判断任意两点是否连通
按照 Floyd 的过程,逐个加入点判断一下。
只是此时的边的边权变为 \(1/0\),而取 \(min\)变成了与运算。
再进一步用 bitset 优化,复杂度可以到 \(O\left(\dfrac{n^3}w\right)\)
for (k=1;k<=n;k++)
for (i=1;i<=n;i++)
for (j=1;j<=n;j++)
f[i][j]|=f[i][k]&f[k][j]; // std::bitset<SIZE> f[SIZE];
for (k = 1; k <= n; k++)
for (i = 1; i <= n; i++)
if (f[i][k]) f[i] = f[i] & f[k];开一个pre数组,在更新距离的时候记录下来后面的点是如何转移过去的,算法结束前再递归地输出路径即可。
比如 Floyd 就要记录pre[i][j] = k;,Bellman-Ford 和 Dijkstra 一般记录 pre[v] = u 。
倍增
void dfs(int u,int ff){
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=ff) f[v][0]=u,dep[v]=dep[u]+1,dfs(v,u);
}
void doubling(){
for(int j=1;j<=20;++j)
for(int i=1;i<=n;++i)
if(dep[i]>=1<<j) f[i][j]=f[f[i][j-1]][j-1];
}
int LCA(int x,int y){
if(dep[x]>dep[y]) swap(x,y);
for(int i=20;i>=0;--i)
if(dep[f[y][i]]>=dep[x]) y=f[y][i];
if(x==y) return x;
for(int i=20;i>=0;--i)
if(f[x][i]^f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}仓鼠找sugar:如果两条路径相交 那么一定有一条路径的LCA在另一条路径上 判断一个点\(x\)是否在路径\(s->t\)上:\(dep[x]>=dep[LCA(s,t)],LCA(s,x)=x或LCA(t,x)=x\)
两遍dfs
int s,mxl,len[N];
void dfs(int u,int ff){
if(len[u]>mxl) s=u,mxl=f[u];
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=ff) len[v]=len[u]+e[i].w,dfs(v,u);
}
int main(){
......
memset(len,0,sizeof(len)),mxl=-1,dfs(1,0);
memser(len,0,sizeof(len)),mxl=-1,dfs(s,0);
return 0;
}树形dp
int mxl,f[N][2];
void dfs(int u,int ff){
f[u][0]=f[u][1]=0;
for(int i=head[u],v,dis;i;i=e[i].nxt)
if((v=e[i].v)!=ff){
dfs(v,u);
dis=f[v][0]+e[i].w;
if(dis>f[u][0]) f[u][1]=f[u][0],f[u][0]=dis;
else if(dis>f[u][1]) f[u][1]=dis;
mxl=max(mxl,f[u][0]+f[u][1]);
}
}以树的重心为根时,所有的子树的大小都不超过整个树大小的一半
找到一个点,其所有的子树节点数最少,那么这个点就是这棵树的重心
可通过两次dfs求出,第一遍求出每个点的子树\(sz_x\) 第二遍找出使\(max_{v\in son_u}\{n-sz_u,sz_v\}\)最小的节点
性质:树中所有点到某个点的距离和中,到中心的距离和是最小的;若有两个重心,那么他们的距离和都一样
int ans,siz=inf;
void dfs(int u,int ff){
sz[u]=1;int res=0;
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=ff) dfs(v,u),sz[u]+=sz[v],res=max(res,son[v]);
res=max(res,n-sz[u]);
if(res<siz) ans=u,siz=res;
}kruskal
int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
void kruskal(){
for(int i=1;i<=n;++i) f[i]=i;
for(int i=1,u,v,cnt=0;i<=m;++i)
if(find(u=e[i].u)!=find(v=e[i].v)){
f[f[u]]=f[v],sum+=e[i].w;
if(++cnt==n-1) return;
}
}prim
priority_queue<pii,vector<pii>,greater<pii> >q;
void prim(){
memset(vis,0,sizeof(vis)),memset(dis,inf,sizeof(dis));
q.push(make_pair(dis[1]=0,1));
while(!q.empty()){
int u=q.top().second;q.pop();
if(vis[u]) continue;
ans+=dis[u],vis[u]=1;
for(int i=head[u],v;i;i=e[i].nxt)
if(!vis[v=e[i].v]&&dis[v]>e[i].w) q.push(make_pair(dis[v]=e[i].w,v));
}
}有向图
int idx=0,Bcnt=0,St[N],dfn[N],low[N],bl[N],sz[N];bool inst[N];
void tarjan(int u){
dfn[u]=low[u]=++idx,St[++St[0]]=u,inst[u]=1;
for(int i=head[u],v;i;i=e[i].nxt)
if(!dfn[v=e[i].v]) tarjan(v),low[u]=min(low[u],low[v]);
else if(inst[v]&&dfn[v]<low[u]) low[u]=dfn[v];
if(dfn[u]==low[u]){
int v;++Bcnt;
do{
inst[v=St[St[0]--]]=0,bl[v]=Bcnt,++sz[Bcnt];
}while(u!=v);
}
}欧拉图中所有顶点的度数都是偶数 若\(G\)是欧拉图,则它是若干个边不重的圈的并
int k,n,m,ans,match[N];
double link[N][N],vis[N];
bool dfs(int x){
for(int i=1;i<=n;++i){//扫描每个男生
if(link[x][i]&&!vis[i]){//如果能连接 并且i不在当前匈牙利树中
vis[i]=1;
if(!match[i]||dfs(match[i])){match[i]=x;return 1;}
//名花无主或者能腾出空位置来
}
}
return 0;
}
int main(){
while(scanf("%d",&k)!=EOF&&k){
memset(link,0,sizeof(link)),memset(match,0,sizeof(match));
rd(m),rd(n),ans=0;
for(int i=1,x,y;i<=k;++i) rd(x),rd(y),link[x][y]=1;
for(int i=1;i<=m;++i){
memset(vis,0,sizeof(vis));
if(dfs(i)) ++ans;
}
printf("%d\n",ans);
}
return 0;
}queue<int> q;bool vis[N];
bool bfs(){
while(!q.empty()) q.pop();
memset(vis,0,sizeof(vis));
q.push(s),vis[s]=1,incf[s]=inf;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u],v,w;i;i=e[i].nxt)
if(w=e[i].w&&!vis[v=e[i].v]){
incf[v]=Min(incf[u],w),pre[v]=i;
q.push(v),vis[v]=1;
if(v==t) return 1;
}
}
return 0;
}
void upd(){
int x=t;
while(x!=s){
int i=pre[x];
e[i].w-=incf[t],e[i^1].w+=incf[t],x=e[i^1].v;
}
maxflow+=incf[t];
}
int main(){
rd(n),rd(m),rd(s),rd(t);
for(int i=1,u,v,w;i<=m;++i) rd(u),rd(v),rd(w),add(u,v,w),add(v,u,0);
while(bfs()) upd();
printf("%d",maxflow);
return 0;
}int head[N],tot=1;
struct edge{int v,flo,cos,nxt;}e[M<<1];
void add(int u,int v,int flo,int cos){
e[++tot]=(edge){v,flo,cos,head[u]},head[u]=tot;
e[++tot]=(edge){u,0,-cos,head[v]},head[v]=tot;
}
int dis[N];
queue<int>q;bool vis[N];
bool spfa(){
memset(vis,0,sizeof(vis)),memset(dis,inf,sizeof(dis));
q.push(s),vis[s]=1,dis[s]=0,incf[s]=inf;
while(!q.empty()){
int u=q.front();q.pop(),vis[u]=0;
for(int i=head[u],v,flo,cos;i;i=e[i].nxt)
if((flo=e[i].flo)&&dis[v=e[i].v]>dis[u]+(cos=e[i].cos)){
dis[v]=dis[u]+cos,pre[v]=i,incf[v]=Min(incf[u],flo);
if(!vis[v]) q.push(v),vis[v]=1;
}
}
return dis[t]!=inf;
}
void upd(){
int x=t;
while(x!=s){
int i=pre[x];
e[i].flo-=incf[t],e[i^1].flo+=incf[t],x=e[i^1].v;
}
mxflo+=incf[t],mncos+=incf[t]*dis[t];
}
int main(){
rd(n),rd(m),rd(s),rd(t);
for(int i=1,u,v,w,z;i<=m;++i) rd(u),rd(v),rd(w),rd(z),add(u,v,w,z);
while(spfa()) upd();
printf("%d %d",mxflo,mncos);
return 0;
}void exgcd(ll a,ll b,ll &x,ll &y){
if(!b){x=1,y=0;return;}
exgcd(b,a%b,x,y);
ll t=x;x=y,y=t-(a/b)*y;
}void exgcd(int a,int b,int &d,int &x,int &y){
if(b) exgcd(b,a%b,d,y,x),y-=x*(a/b);
else d=a,x=1,y=0;
}void prime(int N){
memset(prime,0,sizeof(prime));
memset(v,0,sizeof(v));
for(int i=2;i<=N;++i){
if(!v[i]) v[i]=i,prime[++num_prime]=i;
for(int j=1;j<=num_prime&&i*prime[j]<=n;++j)
v[i*prime[j]]=prime[j];
if(!(i%prime[j])) break;
}
}1、给定y、z、p,计算y^z mod p 的值;
2、给定y、z、p,计算满足xy ≡z(mod p)的最小非负整数x;
3、给定y、z、p,计算满足y^x ≡z(mod p)的最小非负整数x。
第一个要求直接快速幂
第二个要求因为保证P为质数 直接费马小定理求逆元然后*z
第三个就是BSGS模板
const int N=10000+5,M=20000+5,INF=1e9+7,inf=0x3f3f3f3f;
int y,z,p;
int qpow(int a,int b){
int res=1;
while(b){
if(b&1) res=(ll)a*res%p;
a=(ll)a*a%p,b>>=1;
}
return res;
}
map<int,int>hash;
int BSGS(){
hash.clear();y%=p,z%=p;
if(!y) return -1;
int t=(int)sqrt(p)+1;
for(int j=0,val;j<t;++j)
val=(ll)z*qpow(y,j)%p,hash[val]=j;
y=qpow(y,t);
if(!y) return !z?1:-1;
for(int i=0,val,j;i<=t;++i){
val=qpow(y,i);
j=hash.find(val)==hash.end()?-1:hash[val];
if(j>=0&&i*t-j>=0) return i*t-j;
}
return -1;
}
void work2(){
if(!(y%p)&&z%p) puts("Orz, I cannot find x!");
else printf("%lld\n",(ll)qpow(y,p-2)*z%p);
}
void work3(){
int ans=BSGS();
if(ans==-1) puts("Orz, I cannot find x!");
else printf("%d\n",ans);
}
int main(){
int T,K;rd(T),rd(K);
while(T--){
rd(y),rd(z),rd(p);
if(K==1) printf("%d\n",(qpow(y,z))%p);
else if(K==2) work2();
else work3();
}
return 0;
}如果是询问指令,输出一行,仅包含一个整数,表示在同一列上第\(i\)号战舰与第\(j\)号战舰之间布置的战舰数目。如果第\(i\)号战舰与第\(j\)号战舰当前不在同一列上,则输出\(-1\) 带权并查集
int d[N],sz[N];
int find(int x){
if(x==f[x]) return x;
int rt=find(f[x]);
d[x]+=d[f[x]];
return f[x]=rt;
}
void Merge(int x,int y){f[x=find(x)]=y=find(y),d[x]=sz[y],sz[y]+=sz[x];}
int main(){
int T,x,y;char opt[5];
rd(T);
for(int i=1;i<=30000;++i) f[i]=i,sz[i]=1;
while(T--){
scanf("%s",opt);rd(x),rd(y);
if(opt[0]=='M') Merge(x,y);
else{
if(find(x)!=find(y)) puts("-1");
else printf("%d\n",Abs(d[x]-d[y])-1);
}
}
return 0;
}按轶合并
int size[N]; //记录子树的大小
void Union(int x, int y) {
int xx = find(x),yy = find(y);
if (xx == yy) return;
if (size[xx] > size[yy]) swap(xx, yy);
fa[xx] = yy,size[yy] += size[xx];
}开三倍x 自身 x+2n 猎物 x+3n 天敌
int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
void Union(int x,int y) {f[find(y)]=find(x);}
int main(){
rd(n),rd(k);
for(int i=1;i<=n*3;++i) f[i]=i;
for(int i=1,op,x,y;i<=k;++i){
rd(op),rd(x),rd(y);
if(x>n||y>n) {++ans;continue;}
if(op==1){
if(find(x+n)==find(y)||find(x+2*n)==find(y)) ++ans;//为猎物 为天敌
else Union(x,y),Union(x+n,y+n),Union(x+2*n,y+2*n);
}
else{
if(x==y) {++ans;continue;}
if(find(x)==find(y)||find(x)==find(y+n)) ++ans;//为同类 为猎物
else Union(x,y+2*n),Union(x+n,y),Union(x+2*n,y+n);
}
}
printf("%d",ans);
return 0;
}\(lowbit(x)\)表示非负整数\(x\)在二进制表示下“最低位的\(1\)及其后面所有的\(0\)”所构成的数值
struct node{int w,id;}a[N],b[N];
bool cmp(node x,node y){return x.w<y.w;}
int query(int x){int ret=0;while(x>0)ret=(ret+t[x])%P,x-=(x&(-x));return ret;}
void upd(int x){while(x<=n)++t[x],x+=(x&(-x));}
int main(){
rd(n);
for(int i=1;i<=n;++i) rd(a[i].w),a[i].id=i;
for(int i=1;i<=n;++i) rd(b[i].w),b[i].id=i;
sort(a+1,a+n+1,cmp),sort(b+1,b+n+1,cmp);
for(int i=1;i<=n;++i) c[a[i].id]=b[i].id;
for(int i=n;i;--i)
upd(c[i]),ans=(ans+query(c[i]-1))%P;
printf("%d",ans);
return 0;
}noip2013火柴排队 mergesort
c[a[i].id]=b[i].id得理解 \(c[i]\)中\(i\)对应\(a\)中第\(i\)小的数的位置,\(c[i]\)对应\(b\)中第\(i\)小的数的位置 排完序后\(c[i]=i\)即\(a\)中第\(i\)小的数的位置与中第\(i\)小的数的位置相同
struct node{int w,id;}a[N],b[N];
bool cmp(node x,node y){return x.w<y.w;}
void mergesort(int l,int r){
if(l>=r) return;
int mid=l+r>>1,pl=l,pr=mid+1,k=l;
mergesort(l,mid),mergesort(mid+1,r);
while(pl<=mid&&pr<=r)
if(c[pl]<=c[pr]) rk[k++]=c[pl++];
else rk[k++]=c[pr++],ans=(ans+mid-pl+1)%P;
while(pl<=mid) rk[k++]=c[pl++];
while(pr<=r) rk[k++]=c[pr++];
for(int i=l;i<=r;++i) c[i]=rk[i];
}
int main(){
rd(n);
for(int i=1;i<=n;++i) rd(a[i].w),a[i].id=i;
for(int i=1;i<=n;++i) rd(b[i].w),b[i].id=i;
sort(a+1,a+n+1,cmp),sort(b+1,b+n+1,cmp);
for(int i=1;i<=n;++i) c[a[i].id]=b[i].id;
mergesort(1,n);
printf("%d",ans);
return 0;
}询问区间最值
int query(int x,int y){
int s=lg[y-x+1];
return max(f[x][s],f[y-cm[s]+1][s]);
}
int main(){
for(int i=1;i<=n;++i) rd(a[i]);lg[0]=-1,cm[0]=1;
for(int i=1;i<=20;++i) cm[i]=cm[i-1]<<1;
for(int i=1;i<=n;++i) f[i][0]=a[i],lg[i]=lg[i>>1]+1;
for(int j=1;j<=20;++j)
for(int i=1;i+cm[j]-1<=n;++i) f[i][j]=Max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}#### [SP1716 GSS3 - Can you answer these queries III]
动态查询最大子段和+单点修改
struct SegmentTree{int sum,lmx,rmx,mxs;}tree[N];
void pushup(int o){
tree[o].sum=tree[lson].sum+tree[rson].sum;
tree[o].lmx=Max(tree[lson].lmx,tree[lson].sum+tree[rson].lmx);
tree[o].rmx=Max(tree[rson].rmx,tree[rson].sum+tree[lson].rmx);
tree[o].mxs=Max(Max(tree[lson].mxs,tree[rson].mxs),tree[lson].rmx+tree[rson].lmx);
}
void buildtree(int o,int l,int r){
if(l==r){tree[o].sum=tree[o].lmx=tree[o].rmx=tree[o].mxs=a[l];return;}
int mid=l+r>>1;
buildtree(lson,l,mid),buildtree(rson,mid+1,r);
pushup(o);
}
void modify(int o,int l,int r,int x,int k){
if(l==r){tree[o].sum=tree[o].lmx=tree[o].rmx=tree[o].mxs=k;return;}
int mid=l+r>>1;
if(x<=mid) modify(lson,l,mid,x,k);
else modify(rson,mid+1,r,x,k);
pushup(o);
}
SegmentTree query(int o,int l,int r,int x,int y){
if(x<=l&&r<=y) return tree[o];
int mid=l+r>>1;
if(y<=mid) return query(lson,l,mid,x,y);
else if(x>mid) return query(rson,mid+1,r,x,y);
else{
SegmentTree ls,rs,ans;
ls=query(lson,l,mid,x,y),rs=query(rson,mid+1,r,x,y);
ans.sum=ls.sum+rs.sum;
ans.lmx=Max(ls.lmx,ls.sum+rs.lmx);
ans.rmx=Max(rs.rmx,rs.sum+ls.rmx);
ans.mxs=Max(Max(ls.mxs,rs.mxs),ls.rmx+rs.lmx);
return ans;
}
}
int main(){
rd(n);
for(int i=1;i<=n;++i) rd(a[i]);
buildtree(1,1,n);rd(q);
for(int i=1,x,y,op;i<=q;++i){
rd(op),rd(x),rd(y);
if(op==1) printf("%d\n",query(1,1,n,x,y).mxs);
else modify(1,1,n,x,y);
}
return 0;
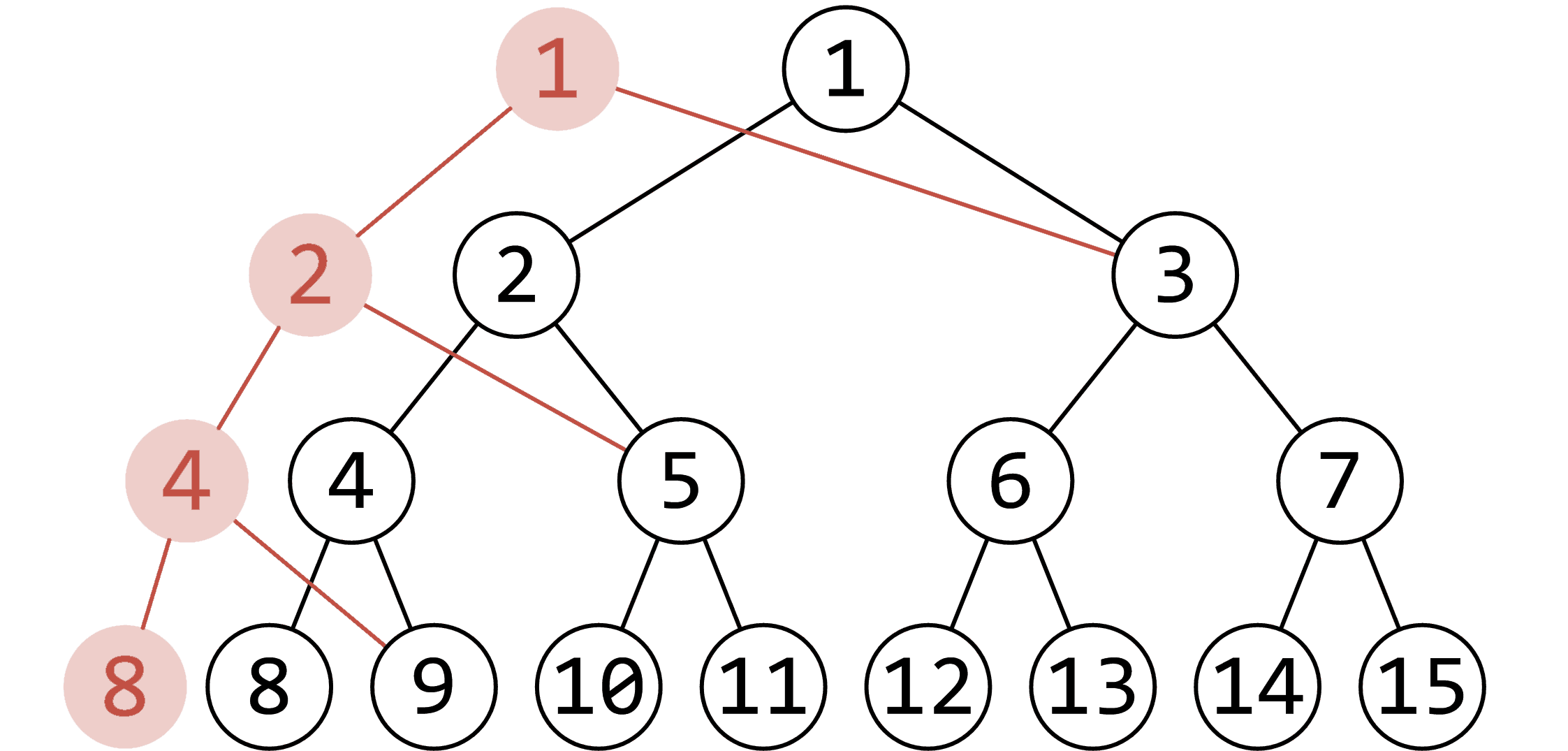
}又理解了一遍== 发现以前只是在背代码 压根不太理解
主席树的主要思想就是:保存每次插入操作时的历史版本,以便查询区间第k小
看图好理解嘿嘿嘿嘿 其实脑抽理解了好久....
只更改了 \(O(log\ n)\)个结点,形成一条链,也就是说每次更改的结点数 = 树的高度。
我们把问题简化一下:每次求 \([1,r]\)区间内的k小值。
怎么做呢?只需要找到插入 r 时的根节点版本,然后用普通权值线段树(有的叫键值线段树/值域线段树)做就行了。
那么这个相信大家很简单都能理解,把问题扩展到原问题——求\([l,r]\)区间k小值。
这里我们再联系另外一个知识理解: 前缀和 。
这个小东西巧妙运用了区间减法的性质,通过预处理从而达到 回答每个询问。
那么我们阔以发现,主席树统计的信息也满足这个性质。
所以……如果需要得到\([l,r]\)的统计信息,只需要用\([1,r]\)的信息减去\([1,l-1]\)的信息就行了。
那么至此,该问题解决!
const int N=2e5+5,M=100+5,inf=0x3f3f3f3f;
int n,m,a[N],w[N],tot=0,tl,rt[N];
struct SegmentTree{int lc,rc,sum;}t[N*50];
void pup(int o){t[o].sum=t[t[o].lc].sum+t[t[o].rc].sum;}
void upd(int &o,int l,int r,int pre,int k){
o=++tot;
if(l==r){t[o].sum=t[pre].sum+1;return;}
int mid=l+r>>1;
if(k<=mid) upd(t[o].lc,l,mid,t[pre].lc,k),t[o].rc=t[pre].rc;
else upd(t[o].rc,mid+1,r,t[pre].rc,k),t[o].lc=t[pre].lc;
pup(o);
}
int query(int l,int r,int x,int y,int k){
if(l==r) return l;
int mid=l+r>>1,ss=t[t[y].lc].sum-t[t[x].lc].sum;
if(ss>=k) return query(l,mid,t[x].lc,t[y].lc,k);
else return query(mid+1,r,t[x].rc,t[y].rc,k-ss);
}
int main(){
rd(n),rd(m);
for(int i=1;i<=n;++i) rd(a[i]),w[i]=a[i];
sort(a+1,a+n+1);
tl=unique(a+1,a+n+1)-a-1;
for(int i=1;i<=n;++i){
w[i]=lower_bound(a+1,a+tl+1,w[i])-a;
upd(rt[i],1,tl,rt[i-1],w[i]);
}
for(int i=1,l,r,k;i<=m;++i)
rd(l),rd(r),rd(k),printf("%d\n",a[query(1,tl,rt[l-1],rt[r],k)]);
return 0;
}struct node{int l,r,id,bl;}q[N];
bool cmp(node A,node B){return (A.bl^B.bl)?A.bl<B.bl:((A.bl&1)?A.r<B.r:A.r>B.r);}
//bool cmp(node A,node B){return A.bl==B.bl?A.r<B.r:A.bl<B.bl;}
void count(int x,int add){
Ans-=(cnt[a[x]]*cnt[a[x]]),cnt[a[x]]+=add;
Ans+=(cnt[a[x]]*cnt[a[x]]);
}
ll gcd(ll a,ll b){
if(a>b) swap(a,b);
return !a?b:gcd(b%a,a);
}
int main(){
rd(n),rd(m),block=sqrt(n);
for(int i=1;i<=n;++i) rd(a[i]);
for(int i=1;i<=m;++i) rd(q[i].l),rd(q[i].r),q[i].id=i,q[i].bl=(q[i].l-1)/block+1;
sort(q+1,q+m+1,cmp);
int l=1,r=0;Ans=0ll;
for(int i=1;i<=m;++i){
while(l<q[i].l) count(l++,-1);
while(l>q[i].l) count(--l,1);
while(r<q[i].r) count(++r,1);
while(r>q[i].r) count(r--,-1);
if(q[i].l==q[i].r) {aa[q[i].id]=0,ab[q[i].id]=1;continue;}
ll x=q[i].r-q[i].l+1;
aa[q[i].id]=Ans-x,ab[q[i].id]=x*(x-1);
}
for(int i=1;i<=m;++i){
ll x=gcd(aa[i],ab[i]);
if(x>0) printf("%lld/%lld\n",aa[i]/x,ab[i]/x);
else printf("%lld/%lld\n",aa[i],ab[i]);
}
return 0;
}void dfs1(int u,int ff){
dep[u]=dep[fa]+1,f[u]=ff,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt)
if((v=e[i].v)!=ff)
dfs1(v,u),sz[u]+=sz[v],(sz[v]>mxs)?(son[u]=v,mxs=sz[v],1):1;
}
void dfs2(int u,int topf){
id[dfn[u]=++idx]=u,top[u]=topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=ff&&v!=son[u]) dfs2(v,v);
}
int LCA(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=f[top[x]];
}
return dep[x]<dep[y]?x:y;
}
int qrange(int x,int y){
int ret=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ret=(ret+query(1,1,n,dfn[top[x]],dfn[x]))%P,x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ret=(ret+query(1,1,n,dfn[x],dfn[y]));
return ret;
}
int qson(int x){return query(1,1,n,dfn[x],dfn[x]+sz[x]-1);}
换根
int findc(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
if(f[top[x]]==y) return top[x];
x=f[top[x]];
}
return dep[x]<dep[y]?son[x]:son[y];
}
int qson(int x){
if(x==rt) return query(1,1,idx,1,idx);
int lca=LCA(x,rt);
if(x!=lca) return query(1,1,n,dfn[x],dfn[x]+sz[x]-1);
int chi=findc(x,rt);
return query(1,1,b,1,n)-query(1,1,n,dfn[chi],dfn[chi]+sz[chi]-1);
}ddp
给定一棵\(n\)个点的树,点带点权。
有\(m\)操作,每次操作给定\(x,y\),表示修改点\(x\)的权值为\(y\) 在每次操作之后求出这棵树的最大权独立集的权值大小。
ll w[N],f[N][2];
int head[N],tot=0;
struct edge{int v,nxt;}e[N<<1];
void add(int u,int v){e[++tot]=(edge){v,head[u]},head[u]=tot;}
int idx=0,dfn[N],id[N],fa[N],son[N],top[N],bot[N],sz[N];
void dfs1(int u,int ff){
fa[u]=ff,sz[u]=1;
for(int i=head[u],v,mxs=-1;i;i=e[i].nxt){
if((v=e[i].v)==ff) continue;
dfs1(v,u),sz[u]+=sz[v];
if(mxs<sz[v]) mxs=sz[v],son[u]=v;
}
}
void dfs2(int u,int topf){
dfn[u]=++idx,id[idx]=u,top[u]=topf;
if(!son[u]) {bot[u]=u;return;}
dfs2(son[u],topf),bot[u]=bot[son[u]];
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=fa[u]&&v!=son[u]) dfs2(v,v);
}
void dfs(int u){
f[u][0]=0,f[u][1]=w[u];
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=fa[u]){
dfs(v);
f[u][0]+=Max(f[v][1],f[v][0]),f[u][1]+=f[v][0];
}
}
struct Matri{
ll a[2][2];
Matri operator*(const Matri &X)const{
Matri c;
memset(c.a,0,sizeof(c.a));
for(int i=0;i<=1;++i)
for(int j=0;j<=1;++j)
for(int k=0;k<=1;++k)
c.a[i][j]=Max(c.a[i][j],a[i][k]+X.a[k][j]);
return c;
}
}val[N],t[N<<2],ans;
void pup(int o){t[o]=t[ls]*t[rs];}
void mdf(int o,int l,int r,int x){
if(l==r){t[o]=val[l];return;}
int mid=l+r>>1;
if(x<=mid) mdf(ls,l,mid,x);
else mdf(rs,mid+1,r,x);
pup(o);
}
Matri query(int o,int l,int r,int x,int y){
if(x<=l&&r<=y) return t[o];
int mid=l+r>>1;
if(y<=mid) return query(ls,l,mid,x,y);
if(x>mid) return query(rs,mid+1,r,x,y);
return query(ls,l,mid,x,y)*query(rs,mid+1,r,x,y);
}
void build(int o,int l,int r){
if(l==r){
int u=id[l];ll g0=0,g1=w[u];
for(int i=head[u],v;i;i=e[i].nxt)
if((v=e[i].v)!=fa[u]&&v!=son[u])
g0+=Max(f[v][0],f[v][1]),g1+=f[v][0];
val[l]=t[o]=(Matri){g0,g0,g1,-inf};
return;
}
int mid=l+r>>1;
build(ls,l,mid),build(rs,mid+1,r);
pup(o);
}
void Mdf(int x,int k){
val[dfn[x]].a[1][0]+=k-w[x],w[x]=k;
while(x){
Matri a=query(1,1,n,dfn[top[x]],dfn[bot[x]]),b;
mdf(1,1,n,dfn[x]);
b=query(1,1,n,dfn[top[x]],dfn[bot[x]]);
x=fa[top[x]];if(!x) return;
int nw=dfn[x];
ll g0=a.a[0][0],g1=a.a[1][0],f0=b.a[0][0],f1=b.a[1][0];
val[nw].a[0][0]=val[nw].a[0][1]=val[nw].a[0][0]+Max(f0,f1)-Max(g0,g1),
val[nw].a[1][0]=val[nw].a[1][0]+f0-g0;
}
}
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
#endif
rd(n),rd(m);
for(int i=1;i<=n;++i) rd(w[i]);
for(int i=1,u,v;i<n;++i) rd(u),rd(v),add(u,v),add(v,u);
dfs1(1,0),dfs2(1,1),dfs(1),
build(1,1,idx);
for(int i=1,x,y;i<=m;++i){
rd(x),rd(y);
Mdf(x,y);
ans=query(1,1,n,dfn[1],dfn[bot[1]]);
printf("%d\n",Max(ans.a[0][0],ans.a[1][0]));
}
return 0;
}从\(n\)个物品中选\(k\)个使其\(\frac {\sum a[i]}{\sum b[i]}\) 最大
double check(double l){
double sum=0.0;
for(int i=1;i<=n;++i) d[i]=(double)a[i]-l*b[i];
sort(d+1,d+n+1);
for(int i=n-k+1;i<=n;++i) sum+=d[i];
return sum;
}
int main(){
rd(n),rd(k);
double l=0.0,r=0.0,mid;
for(int i=1;i<=n;++i) rd(a[i]);
for(int i=1;i<=n;++i) rd(b[i]),r=Max(r,1.0*a[i]/b[i]);
while(r-l>=eps){
mid=(l+r)/2;
if(check(mid)>0) l=mid;
else r=mid;
}
printf("%.4lf\n",l);
return 0;
}struct node{int x,y,z;}c[N];
double qdis(int x,int y){return sqrt((double)(1.0*x*x)+(1.0*y*y));}
bool vis[N];
double sum,dis[N],d[N][N];
bool check(double mid){
for(int i=0;i<=n;++i) dis[i]=1e20,d[i][i]=0.0,vis[i]=0;
dis[1]=sum=0.0;
for(int i=1;i<=n;++i)
for(int j=i+1;j<=n;++j) d[i][j]=d[j][i]=b[i][j]-mid*a[i][j];
for(int i=1,u=0;i<=n;++i,u=0){
for(int j=1;j<=n;++j)
if(!vis[j]&&dis[j]<dis[u]) u=j;
vis[u]=1,sum+=dis[u];
for(int v=1;v<=n;++v)
if(!vis[v]) dis[v]=Min(dis[v],d[u][v]);
}
return sum>0;
}
int main(){
while(scanf("%d",&n)!=EOF&&n){
for(int i=1;i<=n;++i) rd(c[i].x),rd(c[i].y),rd(c[i].z);
double l=0.0,r=10.0,mid;
for(int i=1;i<=n;++i)
for(int j=i+1;j<=n;++j)
a[i][j]=a[j][i]=qdis(c[i].x-c[j].x,c[i].y-c[j].y),b[i][j]=b[j][i]=(double)Abs(c[i].z-c[j].z);//,r=Max(r,b[i][j]/a[i][j])
while(r-l>=eps){
mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.3f\n",l);
}
return 0;
}找一个环使其点权/边权最大
每次check找一个正环 正环不好找就将其边权改为负值去找负环
int cnt[N];bool vis[N];
queue<int>q;bool vis[N];
bool spfa(){
while(!q.empty()) q.pop();
for(int i=1;i<=n;++i) dis[i]=0.0,cnt[i]=vis[i]=1,q.push(i);//图有可能不连通
while(!q.empty()){
int u=q.front();q.pop(),vis[u]=0;
for(int i=head[u],v;i;i=e[i].nxt)
if(dis[v=e[i].v]>dis[u]+e[i].w){
dis[v]=dis[u]+e[i].w;
if(!vis[v]) q.push(v),vis[v]=1,++cnt[v];
if(cnt[v]>=n) return 1;
}
}
return 0;
}
bool check(double x){
memset(head,0,sizeof(head)),tot=0;
for(int i=1;i<=m;++i) add(fr[i],to[i],-((double)a[to[i]]-x*co[i]));
if(spfa()) return 1;//找到负环
else return 0;
}
int main(){
rd(n),rd(m);
for(int i=1;i<=n;++i) rd(a[i]);
for(int i=1;i<=m;++i) rd(fr[i]),rd(to[i]),rd(co[i]);
double l=0.0,r=3000.0,mid;
while(r-l>=eps){
mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.2f",l);
return 0;
}记得初始化值为极小
double d[N],f[N][M];
bool check(double mid){
for(int i=0;i<=n;++i){
if(i) d[i]=(double)a[i]-mid*b[i];
for(int j=0;j<=W;++j) f[i][j]=-INF;
}
f[0][0]=0.0;
for(int i=1;i<=n;++i)
for(int j=0;j<=W;++j) f[i][j]=Max(f[i][j],f[i-1][j]),
f[i][Min(W,j+b[i])]=Max(f[i][Min(W,j+b[i])],f[i-1][j]+d[i]);
return f[n][W]>0;
}
int main(){
rd(n),rd(W);
double l=0.0,r=0.0,mid;
for(int i=1;i<=n;++i) rd(b[i]),rd(a[i]),r=Max(r,(double)a[i]/b[i]);
while(r-l>=eps){
mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%d",(int)(l*1000));
return 0;
}保安站岗
每个点有三种状态 自己覆盖自己 被父亲覆盖 被儿子覆盖
然后要注意被儿子覆盖时的转移 最后如果都是儿子被孙子覆盖的花费更少的话 得选一个儿子自己覆盖自己花费最少的来覆盖 最后输出根节点中自己覆盖自己和被儿子覆盖中较小的一个
int head[N],tot=0;
struct edge{int v,nxt,w;}e[N<<1];
void add(int u,int v){e[++tot].v=v,e[tot].nxt=head[u],head[u]=tot;}
void dp(int u,int ff){
f[u][0]=a[u],f[u][1]=f[u][2]=0;
bool yes=0;int minc=inf;
for(int i=head[u];i;i=e[i].nxt)
if((v=e[i].v)!=ff){
dp(v,u);
f[u][0]+=min(f[v][1],min(f[v][0],f[v][2]));//自己覆盖自己
f[u][1]+=min(f[v][0],f[v][2]);//被父亲覆盖
f[u][2]+=min(f[v][0],f[v][2]) ;//被儿子覆盖
if(f[v][0]<=f[v][2]) yes=1;
else minc=min(minc,f[v][0]-f[v][2]);
}
if(!yes) f[u][2]+=minc;
}
int main(){
rd(n);
for(rg int i=1;i<=n;++i){
rd(i),rd(a[i]),rd(ns);
for(rg int j=1;j<=ns;++j) rd(s),add(i,s),add(s,i);
}dp(1,0);
printf("%d",min(f[1][0],f[1][2]));
return 0;
}染色
关路灯
一条路线上安装了n盏路灯,每盏灯的功率(即同一段时间内消耗的电量有多有少)。老张就住在这条路中间某一路灯旁,他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯
他每天都是在天亮时首先关掉自己所处位置的路灯,然后可以向左也可以向右去关灯,可以中间调头
现在已知老张走的速度为1m/s,每个路灯的位置(是一个整数,即距路线起点的距离,单位:m)、功率(W),老张关灯所用的时间很短而可以忽略不计。 求耗电最少
int main(){
rd(n),rd(s);
for(int i=1;i<=n;++i) rd(pos[i]),rd(w[i]),sum+=w[i];
for(int i=1;i<=n;++i)
for(int j=i;j<=n;++j) t[i][j]=t[i][j-1]+w[j];
for(int i=1;i<=n;++i)
for(int j=i;j<=n;++j) t[i][j]=sum-t[i][j];
memset(f,inf,sizeof(f));
f[s][s][0]=f[s][s][1]=0;
for(int l=2;l<=n;++l)//枚举长度
for(int i=1,j;i<=n-l+1;++i){//枚举左端点
j=l+i-1;
f[i][j][0]=Min(f[i+1][j][0]+t[i+1][j]*(pos[i+1]-pos[i]),f[i+1][j][1]+t[i+1][j]*(pos[j]-pos[i]));
f[i][j][1]=Min(f[i][j-1][1]+t[i][j-1]*(pos[j]-pos[j-1]),f[i][j-1][0]+t[i][j-1]*(pos[j]-pos[i]));
}
printf("%d",Min(f[1][n][0],f[1][n][1]));
return 0;
}不要62
void pre(){
for(int i=0;i<=9;++i) f[1][i]=(!(i==4));
for(int i=2;i<=8;++i)
for(int j=0;j<=9;++j){
if(j==4) {f[i][j]=0;continue;}
for(int k=0;k<=9;++k)
if(!(k==4||j==6&&k==2)) f[i][j]+=f[i-1][k];
}
}
ll solve(ll xx){
ll p=0,num[20],sum=0;
while(xx) num[++p]=xx%10,xx/=10;
num[p+1]=0;
for(int i=p;i>0;--i){
for(int j=0;j<num[i];++j)
if(!(j==2&&num[i+1]==6)) sum+=f[i][j];
if(num[i]==4||(num[i]==2&&num[i+1]==6)) break;
}
return sum;
}
int main(){
pre();
while(scanf("%lld%lld",&a,&b)==2&&a&&b) printf("%lld\n",solve(b+1)-solve(a));
return 0;
}题中已知条件有物品的重量\(w_i\),价值\(v_i\),背包总容量\(W\)
f[i][j]为在只能放前\(i\)个物品的情况下,容量为\(j\)的背包所能达到最大总价值
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
滚动数组优化为一维:f[i]表示处理到当前物品时背包容量为\(i\)的最大价值 f[i]=max(f[i],f[i-w[i]]+v[i])
for(int i=1;i<=n;++i)
for(int j=W;j>=w[i];--j)
f[j]=max(f[j],f[j-w[i]]+v[i]);即01背包中物品的个数变为无数个
for(int i=1;i<=n;++i)
for(int j=w[i];j<=W;++j)
f[j]=max(f[j],f[j-c[i]]+w[i]);即01背包中每种物品可选\(k_i\)次
二进制拆分法
单调队列
混合背包
混合背包就是将前面三种的背包问题混合起来,有的只能取一次,有的能取无限次,有的只能取 次。
for (循环物品种类) {
if (是 0 - 1 背包) 套用 0 - 1 背包代码;
else if (是完全背包) 套用完全背包代码;
else if (是多重背包) 套用多重背包代码;
}二维费用背包
0-1 背包问题,可是不同的是选一个物品会消耗两种价值(经费、时间)方程基本不用变,只需再开一维数组,同时转移两个价值就行了!(完全、多重背包同理)
这时候就要注意,再开一维存放物品编号就不合适了,因为容易 MLE。
for (int k = 1; k <= n; k++) {
for (int i = m; i >= mi; i--) //对经费进行一层枚举
for (int j = t; j >= ti; j--) //对时间进行一层枚举
dp[i][j] = max(dp[i][j], dp[i - mi][j - ti] + 1);
}分组背包即:物品分组,每组的物品相互冲突,最多只能选一个物品放进去。
其实就是从“在所有物品中选择一件”变成了“从当前组中选择一件”,于是就对每一组进行一次 0-1 背包就可以了。
可以将\(t[k][i]\)表示第\(k\)组的第\(i\)件物品的编号是多少,再用\(cnt_k\)表示第\(k\)组物品有多少个。
for (int k = 1; k <= ts; k++) //循环每一组
for (int i = m; i >= 0; i--) //循环背包容量
for (int j = 1; j <= cnt[k]; j++) //循环该组的每一个物品
if (i >= w[t[k][j]])
dp[i] = max(dp[i],
dp[i - w[t[k][j]]] + c[t[k][j]]); //像0-1背包一样状态转移 这里要注意: 一定不能搞错循环顺序 ,这样才能保证正确性。
求失去第\(i\)个物品装满背包有几种方法
在转移的时候是\(f[v]+=f[v-a[i]]\)这样统计的体积为\(a[i]\)的贡献值
int main(){
rd(n),rd(m);f[0][0]=1;
for(int i=1;i<=n;++i){
rd(a[i]),f[0][i]=1;
for(int v=m;v>=a[i];--v) f[v][0]=(f[v][0]+f[v-a[i]][0])%10;
}
for(int i=1;i<=n;++i){
for(int v=1;v<=m;++v)
if(v>=a[i]) f[v][i]=(f[v][0]-f[v-a[i]][i]+10)%10;
else f[v][i]=f[v][0];
for(int v=1;v<=m;++v) printf("%d",f[v][i]);puts("");
}
return 0;
}问有多少种方案使得无法装入剩下的任意一个物品
不能再装即=最小的也装不进去 枚举不在背包中的最小值 然后比它小的肯定都装进去了 比它大的装不进去
int main(){
rd(T);
for(int t=1;t<=T;++t){
memset(f,0,sizeof(f));
rd(n),rd(m),mn=inf,ans=sum[0]=0,f[0]=1;
for(int i=1;i<=n;++i) rd(a[i]);
sort(a+1,a+n+1);
for(int i=1;i<=n;++i) sum[i]=sum[i-1]+a[i];
for(int i=n;i>=1;--i)
for(int v=m;v;--v){
if(v-sum[i-1]>=0&&v>m-a[i]) ans+=f[v-sum[i-1]];//加上sum[i-1]的贡献
//比它小的都放进去了 比它大的放不进去
if(v>=a[i]) f[v]+=f[v-a[i]];//统计
}
printf("%d %d\n",t,ans);
}
return 0;
}给定区\([L,R](L≤R≤2147483647,R-L≤1000000)\),计算区间中素数的个数。
int cnt=0,ans=0,prime[50000];bool v[50010];
void primes(){
for(int i=2;i<=50000;++i){
if(!v[i]) v[i]=1,prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<=50000;++j){
v[i*prime[j]]=1;
if(!(i%prime[j])) break;
}
}
}
bool a[N];
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
#endif
primes();
rd(l),rd(r);
for(int i=1;(ll)prime[i]*prime[i]<=r&&i<=cnt;++i)
for(ll j=max(2ll,(l-1)/prime[i]+1)*prime[i];j<=r;j+=prime[i])
a[j-l]=1;
for(ll i=l;i<=r;++i) if(!a[i-l]) ++ans;
printf("%d",ans);
return 0;
}\(\begin{align*}x^2+y^2&=r^2\\y^2&=r^2-x^2\\y&=\sqrt{(r+x)(r-x)}\end{align*}\) 令:\(d=gcd(r+x,r-x)\),则:设\(A=\frac{r-x}d,B=\frac{r+x}d\) 因为\(d\)为\(r+x,r-x\)的最大公约数 所以一定存在\(gcd(A,B)=1,A,B\)互质
将\(A,B\)代回柿子 得:\(y^2=d^2*A*B\) 因为\(d^2,y^2\)为完全平方数 则\(A*B\)一定为完全平方数 又\(gcd(A,B)=1\ \therefore A\not=B\) 则\(A,B\)本身一定为完全平方数
设\(A\)的算术平方根为\(a\),\(B\)的算术平方根为\(b\) 即:\(A=a*a,B=b*b\)
\(\because A\not=B\ \therefore a\not=b\) 令\(a<b\) 所以\(a*a=\frac{r-x}d,b*b=\frac{r+x}d\to a^2+b^2=\frac{2r}d\)
通解:\(x=d\frac{v^2-u^2}2,y=duv,r=\frac{2(v^2+u^2)}2\)
枚举\(2r\)的因子\(d\),对于每个\(d\)用\(O(\sqrt{\frac rd})\)枚举\(u\),带入\(r\)计算出\(v^2\) 计算\(v^2\)是否为完全平方数及\(i,v\)是否互质
ll gcd(ll a,ll b){return !b?a:gcd(b,a%b);}
bool check(ll a,ll b){
ll x=(ll)sqrt(b);
if(x*x==b) return gcd(a,b)==1;
return 0;
}
ll calc(ll d){
ll ret=0;
for(ll a=1;(a*a<<1)<d;++a)
ret+=check(a,d-a*a);
return ret;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
#endif
rd(r),r<<=1;
for(ll d=1;d*d<=r;++d)
if(!(r%d)) ans+=calc(d)+(((d*d)==r)?0:calc(r/d));
printf("%lld",ans);
return 0;
}N条木板需要被粉刷。 每条木板被分为M个格子。 每个格子要被刷成红色或蓝色。
每次粉刷,只能选择一条木板上一段连续的格子涂上一种颜色。 每个格子最多只能被粉刷一次。
如果只能粉刷 T 次,最多能正确粉刷多少格子?一个格子如果未被粉刷或粉刷错颜色,就算错误粉刷。
所以就先想只有一条木板怎么做 即\(f[i][j]\)表示前\(i\)个格子刷\(j\)次最多能刷正确多少个格子
然后很容易就能想到n条木板就可以将其进行01背包来算最多能刷正确有多少个格子
int main(){
rd(n),rd(m),rd(t);
memset(f,0,sizeof(f));
for(int x=1;x<=n;++x){
scanf("%s",S+1);
for(int i=1;i<=m;++i) sum[i]=sum[i-1]+(S[i]=='1');
for(int i=1;i<=m;++i)//前i个格子
for(int j=1;j<=i;++j){//涂j次
nw[i][j]=0;
for(int k=0;k<i;++k)//由前k个格子转移过来
nw[i][j]=Max(nw[i][j],nw[k][j-1]+Max(sum[i]-sum[k],i-k-(sum[i]-sum[k])));
}
for(int i=1;i<=t;++i)
for(int j=1;j<=Min(i,m);++j) f[x][i]=Max(f[x][i],f[x-1][i-j]+nw[m][j]);
}
for(int i=1;i<=t;++i) ans=Max(ans,f[n][i]);
printf("%d",ans);
return 0;
}标签:数论 mat 树节点 如何 运算 一段 逆序对 键值 优化
原文地址:https://www.cnblogs.com/lxyyyy/p/11853296.html