标签:标记 节点 tin size 最短路径 实现 header 基本 continue
前置技能:线段树、DFS
当我第一次听到 “树链剖分” 这个算法的时候,感觉它一定很高大上。现在看来,它确实很高大上,不过也十分的 暴力 (个人认为,不喜勿喷)
树链剖分,计算机术语,指一种对树进行划分的算法,它先通过轻重边剖分将树分为多条链,保证每个点属于且只属于一条链,然后再通过数据结构(树状数组、SBT、SPLAY、线段树等)来维护每一条链。
————某度百科
百度百科对什么是树剖已经说的很明白了,接下来我们再了解一下其他的概念。
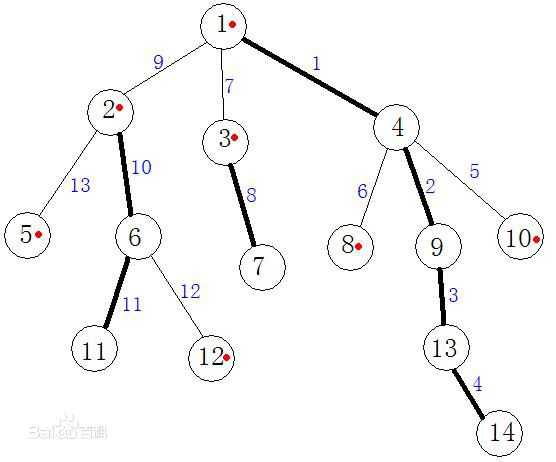
在这张图片中,带红点的就是轻儿子,其余为重儿子;加粗的边为重边,其余的为轻边;\(1 -> 14, \; 2 -> 11, \; 3 -> 7\)的路径为重链,其余的为轻链。
前面某度已经说了,树链剖分要通过轻重边剖分将树分为多条链,那么它是怎么找出轻重边,又是怎么剖分的的呢?不要着急,我们接着讲
先来说一说我们需要求哪些东西
| 变量 | 含义 |
|---|---|
| \(f[i]\) | 结点\(i\)的父亲 |
| \(son[i]\) | 结点\(i\)的重儿子(如果有\(i\)有两个及以上的重儿子,则随便指定一个) |
| \(size[i]\) | 结点\(i\)的子树大小 |
| \(deth[i]\) | 结点\(i\)的深度 |
| \(top[i]\) | 结点\(i\)所在的重链的顶端(若\(i\)为轻儿子,则\(top[i]\)等于它本身) |
| \(pos[i]\) | 结点\(i\)的新编号(可以理解为点\(i\)对应的\(rank\)数组的下标) |
| \(rank[i]\) | 编号\(i\)对应的树上的结点的点权 |
其中,前四个变量可以通过一次\(DFS\)求出,其余三个可以在第一次\(DFS\)的基础上再通过一次\(DFS\)求出
代码是这样滴:
void dfs1(int now,int fa){
f[now]=fa, deth[now]=deth[fa]+1, size[now]=1;
for(int i=head[now];i;i=e[i].nex){
int to=e[i].t;
if(to==fa) continue;
dfs1(to,now);
size[now]+=size[to];
if(size[to]>size[son[now]]) son[now]=to;
}
}
void dfs2(int now,int topp){
top[now]=topp, pos[now]=++dfn, rank[dfn]=a[now];
//a[i]表示结点i的点权
if(!son[now]) return ;
dfs2(son[now],topp);
for(int i=head[now];i;i=e[i].nex){
int to=e[i].t;
if(to!=son[now]&&to!=f[now]) dfs2(to,to);
}
}在我们进行第二次\(DFS\)的时候,我们是优先搜索重儿子,这是为了保证重链在\(rank\)数组里的连续性,除了重链,一颗子树的编号在\(rank\)数组里也是连续的。
为什么要这么做?接下来你就知道了。
到此,我们的树链剖分就讲完了。可是,现在我们求出了这么多东西,它们能干什么呢?
还记得一开始某度百科上说过可以“通过数据结构(树状数组、SBT、SPLAY、线段树等)来维护每一条链”吗?没错,在求出了这么多东西后,我们就可以用我们所熟悉的数据结构来瞎搞这颗树了(大雾
为了方便理解+应用广泛,我们以线段树为例来讲一下树链的维护(其实是因为博主太蒟,只会线段树)
假设题目让我们进行以下操作:
上文我们说过:重链在\(rank\)数组里是连续的,一颗子树在\(rank\)数组里也是连续的。所以我们可以用线段树通过多次区间修改和多次区间查询来搞定这四个操作。
首先是线段树:
其实线段树的一切都没什么变化,该怎么打还是怎么打,只不过要维护的数组变成我们剖出来的\(rank\)数组
代码如下:
void build(int l,int r,int p){ //建树
if(l==r){
tree[p]=rank[l]; return ; //要注意这里的数组是rank
}
build(l,mid,ls); build(mid+1,r,rs);
tree[p]=tree[ls]+tree[rs];
}
void down(int l,int r,int p){ //下传懒标记(我太蒟了,不会标记永久化)
tag[ls]+=tag[p]; tag[rs]+=tag[p];
tree[ls]+=(mid-l+1)*tag[p];
tree[rs]+=(r-mid)*tag[p];
tag[p]=0;
}
void update(int l,int r,int p,int nl,int nr,ll k){ //区间修改
if(nl<=l&&nr>=r){
tag[p]+=k; tree[p]+=(r-l+1)*k;
return ;
}
down(l,r,p);
if(nl<=mid) update(l,mid,ls,nl,nr,k);
if(nr>mid) update(mid+1,r,rs,nl,nr,k);
tree[p]=tree[ls]+tree[rs];
}
ll query(int l,int r,int p,int nl,int nr){ //区间查询
ll ans=0;
if(nl<=l&&nr>=r) return tree[p];
down(l,r,p);
if(nl<=mid) ans+=query(l,mid,ls,nl,nr);
if(nr>mid) ans+=query(mid+1,r,rs,nl,nr);
return ans;
}那这棵线段树该怎么用呢?
如果点\(x\)和\(y\)不在一条重链上,就让它们一直跳,直到跳到一条重链上。为了防止越跳越远,我们让深度更深的先跳到另一条链上。在跳的时候,因为重链在数组中是连续的,我们就可以用线段树进行区间更改/查询来处理这一部分,通过多次区间操作,就能够实现这操作1、2。
void upd(int x,int y,ll k){ //将树从x到y结点最短路径上所有节点的值都加上z
while(top[x]!=top[y]){ //如果不在一条重链上
if(deth[top[x]]<deth[top[y]]) swap(x,y);
update(1,n,1,pos[top[x]],pos[x],k);
x=f[top[x]]; //让更深的跳上来,跳到另一条链上,顺便加上区间修改
}
//如果在一条链上
if(deth[x]>deth[y]) swap(x,y);
update(1,n,1,pos[x],pos[y],k); //则处理一下两节点之间的区间
}
ll sum(int x,int y){ //查询操作和修改是一样的……
ll ans=0;
while(top[x]!=top[y]){
if(deth[top[x]]<deth[top[y]]) swap(x,y);
ans+=query(1,n,1,pos[top[x]],pos[x]);
x=f[top[x]];
}
if(deth[x]>deth[y]) swap(x,y);
ans+=query(1,n,1,pos[x],pos[y]);
return ans;
}对于操作3、4,则更为简单。因为子树在数组中是连续的,我们又知道每棵子树的大小,所以直接一波线段树就可以了
update(1,n,1,pos[x],pos[x]+size[x]-1,y); //将以x为根节点的子树内所有节点值都加上z
query(1,n,1,pos[x],pos[x]+size[x]-1); //求以x为根节点的子树内所有节点值之和到此,树剖就真的讲完了,不知众看官看懂了多少……
以上这些都是一些裸题。树剖本身不难理解,但因为代码较长,比较容易写错……又全是递归,不好调试……所以要多练……
树链剖分原理和实现 —— \(banananana\)
树链剖分详解—— \(ChinHhh\)
树链剖分详解—— \(communist\)
标签:标记 节点 tin size 最短路径 实现 header 基本 continue
原文地址:https://www.cnblogs.com/morslin/p/11854722.html