原文转:http://users.rowan.edu/~polikar/WTpart1.html
六、小波变换基础:傅立叶变换(一)
让我们对前面的内容做个简要回顾。
基本上,我们要用小波变换来处理非平稳信号,即那些频率分量随时间变换而变换的信号。上文我已经说过傅立叶变换不适合处理这些非平稳信号,并且举了例子来来佐证。再做一个快速的回顾吧,看下面这个例子:假定我们有两个不同的信号,再假设他们都有相同的频谱分量,只有一点不同,其中一个信号含有的四个频率分量在整个信号周期内都存在,另外一个也有相同的四个频率分量,但出现的时间各不相同。两个信号的傅立叶变换将会是一样的,如同在文章的第一部分中所讲到的那个例子。虽然这两个信号是完全不同的,但他们的傅立叶变换却是相同的!这一点很明显告诉我们不能用傅立叶变换来处理非平稳信号。但是这是为什么呢?换句话说,为什么完全不同的两个信号却有同样的傅立叶变换呢?傅立叶变换到底是怎么变换的?
信号处理中的一个重要里程碑:傅立叶变换!!
基于以下两个原因,我不想深究傅立叶变换的细节:
1、 这个课题对本教程来说太广了。
2、 它不是我们主要关注的对象。
不过,基于以下原因,我将会在文中涉及一些要点:
1、 为了理解小波变换,你需要傅立叶变换作为背景知识。
2、 它是到目前为止最重要的信号处理工具,已经被用了很多很多年了。
在十九世纪年(或许是1822年,不过你并不需要知道这么确切的时间,相信我,绝对比你能想起来的时间还早得多),法国数学家傅立叶,发现所有周期信号都可以表示为无限的周期复指数函数的和。在他发现了这个著名的周期函数性质之后,其想法被推广到第一个非周期函数,然后是周期和非周期的离散信号。在这之后,傅立叶变换就成了在计算机中非常适合的计算工具。1965年,出现了一个叫做快速傅立叶变换的新算法,从此傅立叶变换更加流行了。
傅立叶变换将信号分解为具有不同频率的复指数函数,可以用以下两个公式来解释它的变换过程:
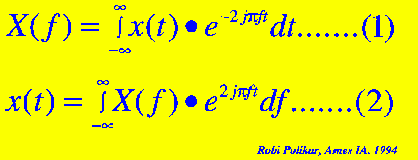
图2.1
在上式中,t表示时间,f表示频率,x表示要分析的信号。注意到x表示信号的时域,X表示信号的频域,这个约定用来区别对信号的两种表示。公式(1)叫做x(t)的傅立叶变换,公式(2)叫做X(f)的傅立叶逆变换,其结果是x(t)。用过傅立叶变换的人对这些已经很熟悉了,但不幸的是,很多人虽然用到了这些公式,却没有理解它的基本原理。现在仔细看公式(1):信号x(t)是一些指数项的累加和,每个项对应特定的频率f,然后在整个时域内整合起来(这里的“整个时域”将在下面进行介绍)。公式(1)中的指数项还可以被写成下面这样:
cos(2.pi.f.t)+j.Sin(2.pi.f.t).......(3)
上面的表达式以一个频率为f的余弦信号作为实部,一个频率为f的正弦信号作为虚部。所以我们实际要做的是用一些复数表达式叠加出原始信号,这些复数表达式包含了频率为的正弦和余弦分部。然后我们对乘积积分,即我们把乘积中的所有的点叠加起来。如果积分结果(只不过某种无限求和)的值很大,那么我们可以这样说:信号x(t)在频率f处有一个大的频谱分量。信号主要是由频率为f的分量组成。如果积分结果的值较小,就意味着信号中频率为f的分量很少。如果积分结果为0,表明信号中根本不存在频率为f的分量。
这里很有意思,让我们看看积分是怎么回事:信号是由一些不同频率的正弦项叠加起来的,如果信号中频率为f的分量幅值较大,那么这个分量就和正弦项重叠,他们的积就会(相对)较大,这表明信号x有一个频率为f的主要分量。
不过,如果信号中不含频率为f的分量,则乘积结果为0,这表明信号没有频率为f的分量。如果频率为f的分量不是信号的主要组成部分,则乘积会(相对)较小。这就说明频率为f的分量在信号中的幅值很小,不是信号中的主要组成分量。现在,请注意方程式(等式1)中的积分随时间变化。公式(1)中左边是一个对频率的函数,因此,(1)式的积分是由每一个频率值f计算出来的。
注意!!因为积分是从负无穷到正无穷,所以积分在所有时间内有效。这说明了不管频率为的分量f何时出现,都将会影响积分结果。换句话说,不管频率为的分量出现在时刻还是以后,都将对积分结果产生相同的影响。这就是为什么傅立叶变换不适合分析随时间变化,频率改变的信号,即非平稳信号。当且仅当频率为f的分量一直存在(对所有的),傅立叶变换得到的结果才有意义。
傅立叶变换可以给出某个频率分量存在与否,其结果不取决于信号出现的时间。需要知道的是,一个平稳的信号才优先用傅立叶变换进行处理。第一部分中给出的例子现在已经讲得很明白了,这里我再次给出:看下式:
x(t)=cos(2*pi*5*t)+cos(2*pi*10*t)+cos(2*pi*20*t)+cos(2*pi*50*t)
信号中含有四个频率分量,所有分量在信号的整个周期内都存在。
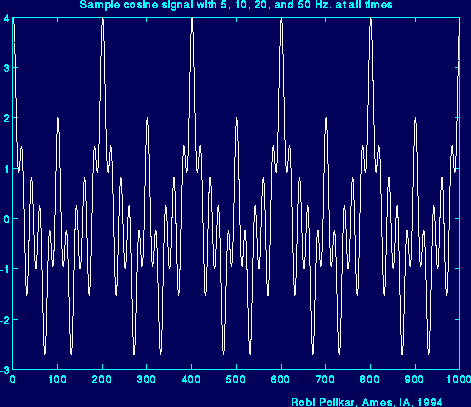
图2.2
这里是它的傅立叶变换。频率轴被剪切过了,因为理论上来说它是无穷的(仅指连续傅立叶变换,实际上我们在这里做的是离散傅立叶变换,频率轴最少要达到采样频率的两倍处,变换过的信号是对称的。不过现在这些都不重要)。
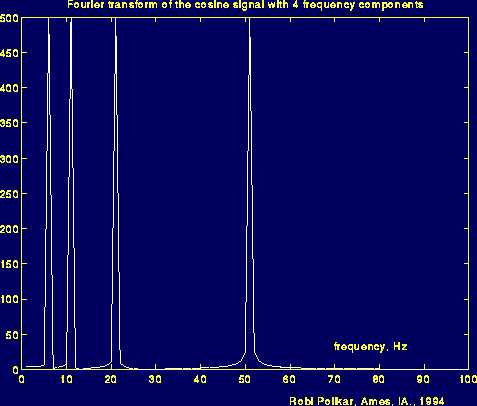
图2.3
上图中出现了四个尖峰,对应四个不同的频率.
现在,看下图,信号是余弦信号,仍然有四个频率分量,不过这四个分量出现在不同时刻:
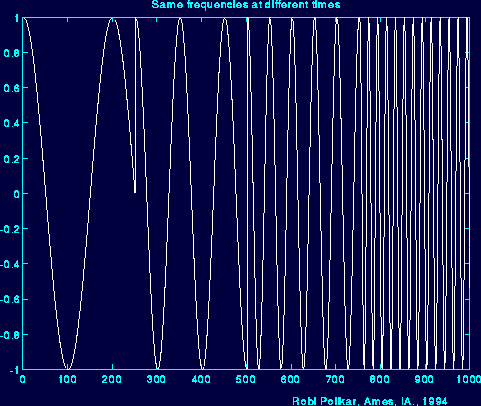
图2.4
下面是它的傅立叶变换:
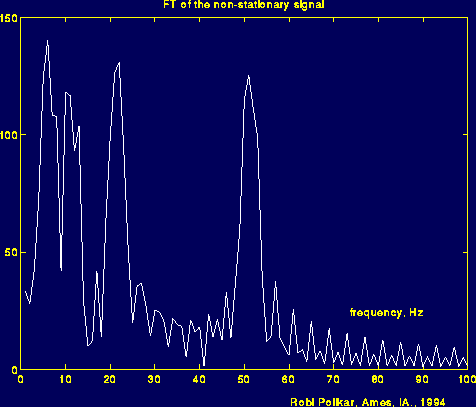
图2.5
在上图中,与你想象的一样,图形与前一个信号的傅立叶变换几乎一样,仔细看,图中也有四个尖峰对应四个频率。我可能把这两张图弄得看起来比较像,但这不并不是有意为之。尖峰中出现的噪声所代表的频率分量在信号中是存在的但是由于它们的幅值很小,不是组成信号的主要分量,我们在图中看到的这些,是由于频率突变产生的。特别注意时域信号在大约250(ms)的时间如何变化(有一些合适的滤波手段可以将频域中的噪声去掉,但是这些与我们要讲的话题无关,如果你需要有更详细的信息,请给我发邮件)。
现在你应该理解了傅立叶变换的基本概念,什么地方可以用什么地方不可以用。正如你从上面的图中所看到的,傅立叶变换不能很好的区分两个信号。傅立叶变换之后的结果基本一致,因为他们都是由相同的频率分量组成的。因此,对非平稳信号来说,例如具有时变性的信号,傅立叶变换并不是一个合适的工具。
请将这个性质记在心里。不幸的是,许多用傅立叶变换的人并不思考这些。他们假定他们处理的信号都是平稳的,但在实际中却经常不是。当然,如果你对频率分量的发生时间不感兴趣,只关心哪些频率分量存在,傅立叶变换还是一个很合适的分析工具。
那么,我们知道了不能用(哦,实际上可以用,但是却不应该用)傅立叶变换处理非平稳信号,我们应该怎么做呢?
还记得吗,我曾经提过小波变换刚刚应用了年左右,你可能会想,那些研究者们是否十年前才注意这种非平稳信号。
很明显不是。
很明显在发现小波变换之前他们还是做了些什么?
是的,他们确实做了些事情。
他们想出了:线性时频表示。
