1. 通过以下观察0-1矩阵，很容易发现以下性质：

• 拥有自反性(reflexive)的0-1矩阵主对角线全为“1”
  
• 拥有非自反性(irreflexive)的0-1矩阵主对角线全为“0”
  
• 拥有对称性(symmetric)的0-1矩阵主对角线任意，关于主对角线对称的元素相等
  
• 拥有反对称性(antisymmetric)的0-1矩阵主对角线任意，关于主对角线对称的元素不能同时为“1”
  

1. 定义两个邻接矩阵的join为这两个矩阵的布尔或运算(boolean ‘or‘)
2. 定义两个邻接矩阵的meet为这两个矩阵的布尔与运算(boolean ‘and‘)

用0-1矩阵表示关系的复合:

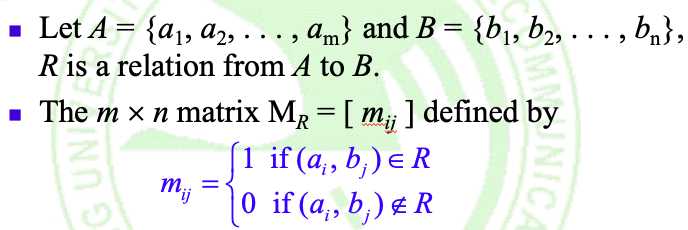
令M_S?R = [t_ij], M_R = [r_ij], M_S = [s_ij]
则M_S?R = M_R⊙M_S
其中，⊙表示两个矩阵进行布尔乘运算(boolean product)

例：

\[ M_R = \left[\begin{matrix} 1 & 0 & 1 \ 1 & 1 & 0 \ 0 & 0 & 0 \end{matrix} \right] \]
\[ and \quad M_S = \left[\begin{matrix} 0 & 1 & 0 \ 0 & 0 & 1 \ 1 & 0 & 1 \end{matrix} \right] \]

则M_S?R的每个t_ij由M_R的第i行与M_S的第j列进行布尔乘运算，得到S?R的邻接矩阵为:
\[ M_{S?R} = \left[\begin{matrix} 1 & 1 & 1 \ 0 & 1 & 1 \ 0 & 0 & 0 \end{matrix} \right] \]

矩阵布尔乘计算器

用图表示关系

理解：

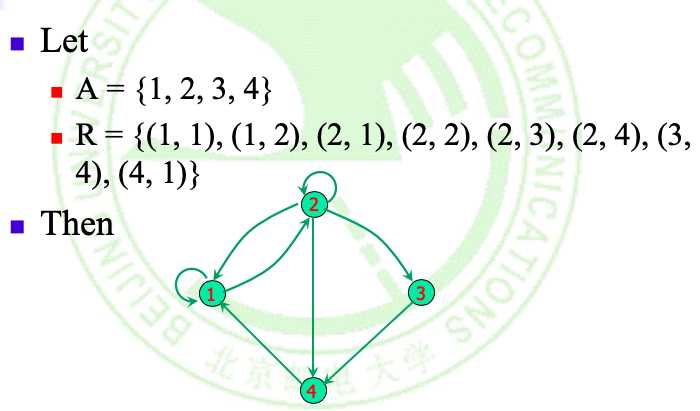
例:用有向图来表示一个关系:

1. 入度与出度

• 顶点a的入度:以顶点a为起点的箭头的个数
  
• 顶点a的出度:以顶点a为终点的箭头的个数
  

1. 限制
   如果R是定义在A上的关系，并且B是A的子集，则R对B的限制(the restriction of R to B)为:

   R ∩ (B × B)

2. 有特殊性质的图

• 具有自反性的图：每个节点都有自环
  
• 具有反自反性的图：无自环节点
  
• 具有对称性的图：所有箭头都是双向的
  

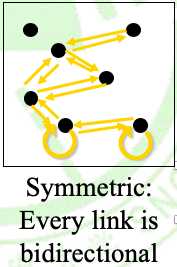
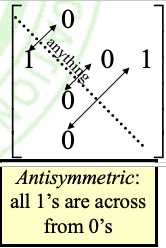
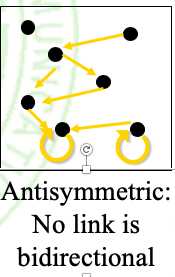
• 具有反对称性的图：无双向箭头
  

• 特别注意:①.没有既不对称又不反对称的图；②.没有既不自反也不反自反的图。

1. 一些等价关系:

有一个关系R以及它的邻接矩阵M_R，设△是一个等价关系，即M_△是单位矩阵

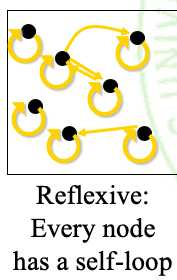
①. R自反 <= => △ ? R <= => all 1‘s on its main diagonal
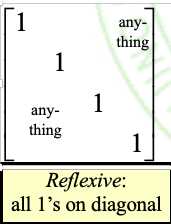
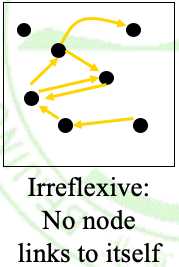
②. R反自反 <= => △ ∩ R = ? <= => all 0‘s on its main diagonal
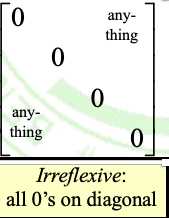
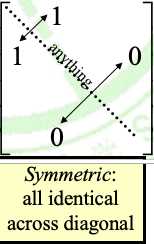
③. R对称反对称非对称显然不赘述
④. R传递 <= => M_R=[m_ij]具有这个性质:如果m_ij = 1，并且m_jk = 1，那么m_ik = 1.
④. R传递 ==> R² ? R, because if a and c are connected by a path of length 2 in R, then they must be connected by a path of length 1.

1. 误区:

The answer is NO!

9.3 关系的表示

标签：顶点   and   表示   邻接   png   title   运算   answer   use   

原文地址：https://www.cnblogs.com/SpicyArticle/p/11868611.html