标签:因此 一个 一般来说 大小 image 中间 而且 哈夫曼 排序
错解:
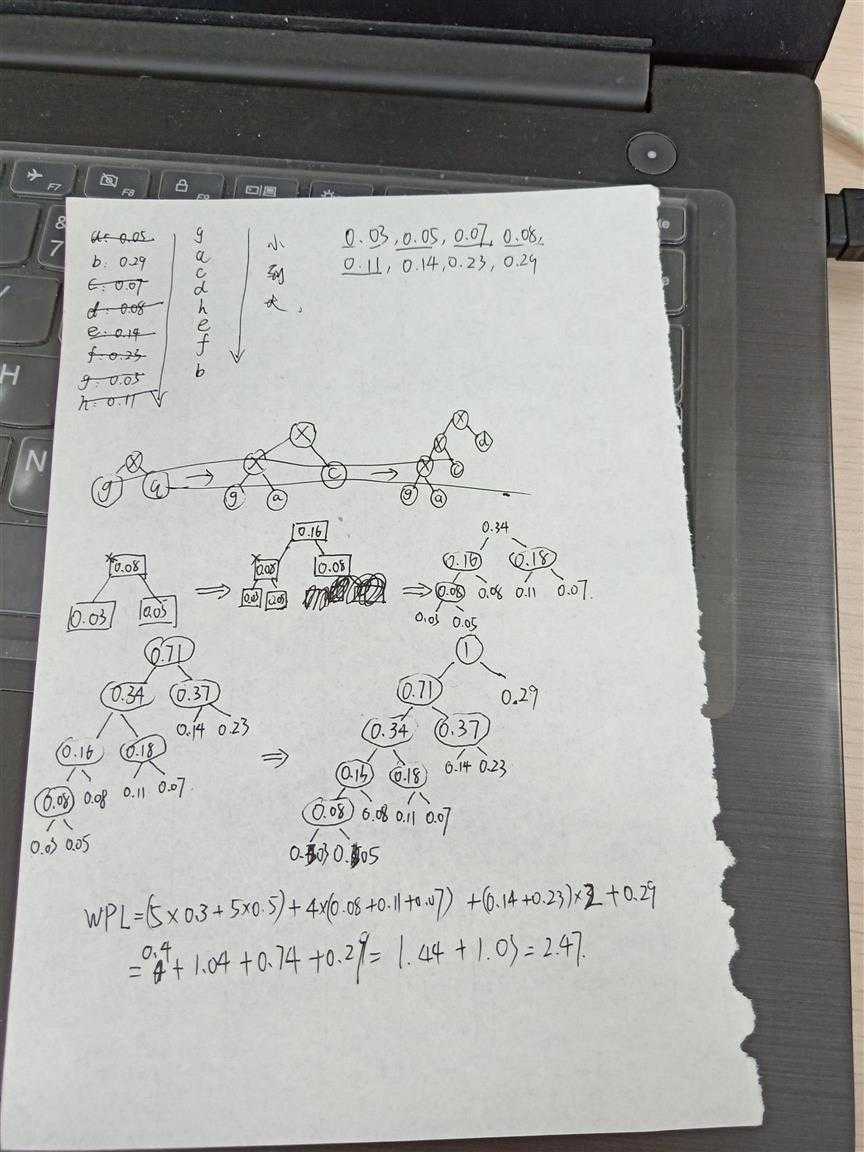
正解:

最优二叉树的构建一般来说都是根据数组从小到大的顺序,从下往上排序。一个父结点就只有两个子结点,而且兄弟结点之间的大小差距应该尽可能小。如果数组中可以找得到差距够小的数字,就直接用数组中的数作为中间结点的兄弟结点(同时也是叶结点),
根据题目中的数据摆放顺序,0.07应该与0.08摆放在一起,之后的0.07+0.08(中间结点)=0.15(中间结点)与0.14比较接近适合放一起,而0.08+0.11=0.19(中间结点)为了遵循大数往上放、小数往下放的原则,如果代替0.14放在0.15的旁边,计算出来的WPL效益肯定不如0.14放在0.15(中间结点)旁边。因此0.08+0.11=0.19(中间结点)可以放在另外一个分支上。
接下来,根据差距小的数字放在一起做兄弟结点的原则,0.14+0.15(中间结点)=0.29(中间结点)与数组中的0.29刚好就可以放在一起,而剩下的0.23就可放在0.19旁边。这样一来数组内的所有数字都摆放完毕,再根据结点的数字计算中间结点的值并连接在一起即可。
标签:因此 一个 一般来说 大小 image 中间 而且 哈夫曼 排序
原文地址:https://www.cnblogs.com/77599aa/p/11869981.html