标签:splay spl 最大值 isp 顶点 图片 ext code math
边长为\(1\)的正方形\(ABCD\)的顶点\(A,D\)分别在\(x\)轴,\(y\)轴的正半轴上滑动,则\(\overrightarrow{OB}\cdot \overrightarrow{OC}\)的最大值为\(\underline{\qquad\qquad}\).
解析:
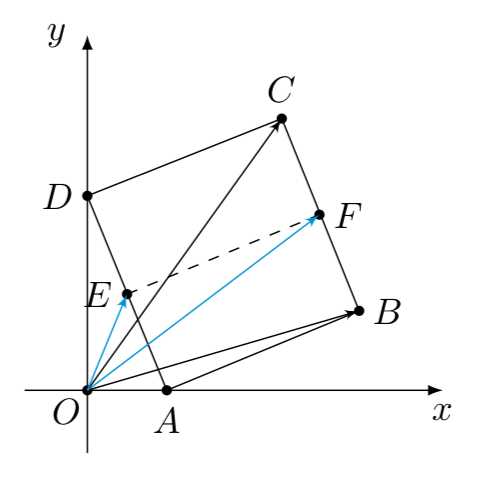
如图,记\(E,F\)分别为\(AD,BC\)的中点,
标签:splay spl 最大值 isp 顶点 图片 ext code math
原文地址:https://www.cnblogs.com/Math521/p/11871556.html