标签:get better tom because 收获 时间 therefore tor round
We now have \(k\) sorted sequences, and we are to merge them into one sorted sequence with the merge algorithm. Our task is to find out the optimal merging order as well as the worst merging order so that the total comparison times for the merging algorithm is the least and the most.
It‘s natural to use the Huffman Tree algorithm to solve the problem. In the task we get the lengths of the sequences, which is a lot like the probabilities of appearance for each character in the Huffman problem. And we merge two sequences each time, which is like picking two characters each time in the Huffman problem.
But since the Huffman algorithm is a greedy algorithm, which is able to find the local optimum of a task but cannot always find the global optimum, we should confirm that the Huffman algorithm can be applied here to find the global minimum and maximum. The global optimum of a task can be found out with the greedy algorithm if the task has the following two features:
It turns out that we can use the same way as the Huffman algorithm to measure if a solution is good. Here‘s the reason. Assume that the total times needed to merge all sequences is \(B(T)\), where \(T\) is the Huffman tree.
Let‘s go through the process of merging the sequences.
The original sequence list which contains sequences to be merged will be:
5 12 11 21. Pick the two smallest sequences and merge them together. According to the formula \(m + n - 1\), the merging time needed for the two sequences will be:
\[2 + 5 - 1 = 6\]
2.1. Add the merged sequence whose length is 7 to the sequence list. The sequence list now is:
7 12 112.2. Pick the two smallest sequences and merge them together. According to the formula \(m + n - 1\), the merging time needed for the two sequences will be:
\[7 + 11 - 1 = 17\]
And the total times will be:
\[
\begin{aligned}
B(T)
&= (2 + 5 - 1) + (7 + 11 - 1) \&= (2 + 5 - 1) + ((2 + 5) + 11 - 1 )
\end{aligned}
\]
3.1. Add the merged sequence whose length is 7 to the sequence list. The sequence list now is:
12 183.2. Pick the two smallest sequences and merge them together. According to the formula \(m + n - 1\), the merging time needed for the two sequences will be:
\[12 + 18 - 1 = 29\]
And the total times will be:
\[
\begin{aligned}
B(T)
&= (2 + 5 - 1) + (7 + 11 - 1) + (12 + 18 - 1) \&= (2 + 5 - 1) + (7 + 11 - 1 ) + (12 + (7 + 11) - 1) \&= (2 + 5 - 1) + ((2 + 5) + 11 - 1) + (12 + ((2 + 5) + 11) - 1)
\end{aligned}
\]
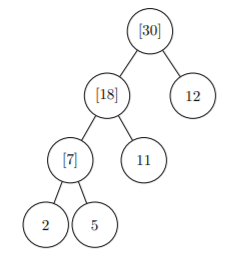
Thus
\[
B(T) = 2 * 3 + 5 * 3 + 11 * 2 + 12 * 1 + (-1) * 3 = 52
\]
And it‘s the minimal solution, according to the question.
The Huffman tree is like:
Obviously it‘s a lot like the way of the Huffman algorithm, except that we have a \((-1) * 3\), where 3 is the depth of the tree. Therefore we can prove the two properties also in the same way as the Huffman algorithm.
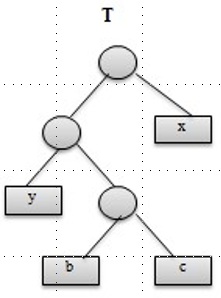
One way to prove the greedy-choice property is pruning. Here‘s what it does:
Assume that we now have an optimal solution \(T\) for the task. In the tree the node \(x\) and \(y\), representing two sequences sorted, have the shortest lengths. According to the greedy algorithm and the proof of the Huffman algorithm they should be two children at the bottom of the tree (but they are not at the bottom in \(T\)).
We now exchange the position of \(x\) and \(b\), so that the new tree is the situation calculated by the greedy choice. Let‘s call it \(T^{'}\).
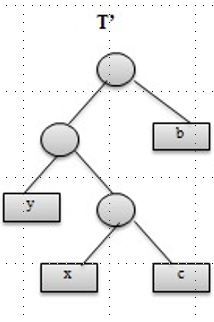
Now we are to prove that the new tree \(T^{'}\) is not worse than the original tree \(T\). In other words, we are to prove that
\[
B(T^{'}) \leq B(T)
\]
that is,
\[
B(T) - B(T^{'}) \geq 0
\]
And since the only difference between the two trees are \(b\) and \(x\),
\[
B(T) - B(T^{'}) = f(b)d_T(b) + f(x)d_T(x) - (f(x)d_{T^{'}}(x) + f(b)d_{T^{'}}(b))
\]
And because
\[
d_{T^{'}}(x) = d_T(b) \d_{T^{'}}(b) = d_T(x) \\]
for that their corresponding positions are the same, we get
\[
\begin{aligned}
B(T) - B(T^{'})
&= f(b)d_T(b) + f(x)d_T(x) - (f(x)d_T(b) + f(b)d_T(x)) \&= f(b)d_T(b) + f(x)d_T(x) - f(x)d_T(b) - f(b)d_T(x) \&= (f(b) - f(x))(d_T(b) - d_T(x))
\end{aligned}
\]
Since \(x\) is the shortest,
\[
f(b) - f(x) \geq 0
\]
And according to tree \(T\)
\[
d_T(b) - d_T(x) > 0
\]
we get
\[
(f(b) - f(x))(d_T(b) - d_T(x)) \geq 0
\]
thus
\[
B(T) - B(T^{'}) \geq 0
\]
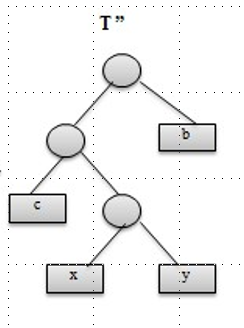
In the same way, when we exchange the position of \(c\) and \(y\) and get a new tree \(T^{''}\), we have
\[
(f(c) - f(y))(d_{T^{'}}(c) - d_{T^{'}}(y)) \geq 0
\]
which is equiavalent to
\[
B(T^{'}) - B(T^{''}) \geq 0
\]
Therefore, we have
\[
B(T) \geq B(T^{'}) \geq B(T^{''})
\]
and since \(T\) is an optimal solution, we get
\[
B(T) \leq B(T^{''})
\]
thus
\[
\left .
\begin{aligned}
B(T) \geq B(T^{'}) \geq B(T^{''}) \B(T) \leq B(T^{''})
\end{aligned}
\right \} B(T^{''}) = B(T)
\]
Therefore we‘ve proved that the tree \(T^{''}\) which is calculated with greedy choices is not worse than the original tree \(T\) which is not calculated with greedy choices.
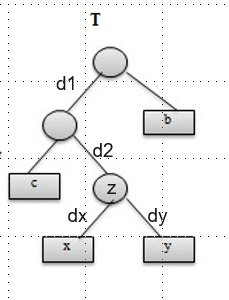
Let‘s say the tree \(T\) here is an optimal solution, and its substructure \(T^{'}\) is the tree without \(x\) and \(y\).
\[ \begin{aligned} f(x)d(x) + f(y)d(y) &\in B(T) \f(x)(d1 + d2 + dx) + f(y)(d1 + d2 + dy) &\in B(T) \f(x)(d1 + d2) + f(x)dx + f(y)(d1 + d2) + f(y)dy &\in B(T) \(f(x) + f(y))(d1 + d2) + f(x)dx + f(y)dy &\in B(T) \f(z)(d1 + d2) &\in B(T) - f(x)dx - f(y)dy \f(z)(d1 + d2) &\in B(T^{'}) \end{aligned} \]
thus
\[
B(T) = B(T^{'}) + f(x)dx + f(y)dy
\]
If \(T^{'}\) is not the optimal substructure, let‘s say the optimal substructure is \(T{''}\). So
\[
B(T^{''}) < B(T^{'})
\]
thus
\[
B(T^{''}) + f(x)dx + f(y)dy < B(T^{'}) + f(x)dx + f(y)dy
\]
and since
\[
B(T) = B(T^{'}) + f(x)dx + f(y)dy
\]
we have
\[ B(T^{''}) + f(x)dx + f(y)dy < B(T) \]
But since \(T\) is the optimal solution, the equation above is wrong. Thus the optimal solution of the task depends on the optimal substructure of the subtask.
The strategy is a lot like the Huffman tree algorithm, as introduced above. To find out the worst solution we should merely find two longest sequences each time instead of two shortest.
int minTotalTimes = 0;
int maxTotalTimes = 0;
for (int i = 1; i <= k - 1; i++) {
// find two shortest sequences
int minTimes1 = qIncreasing.top();
qIncreasing.pop();
int minTimes2 = qIncreasing.top();
qIncreasing.pop();
// add up the times needed
minTotalTimes += minTimes1 + minTimes2 - 1;
// push the merged sequence to the list
qIncreasing.push(minTimes1 + minTimes2);
// find two longest sequences
int maxTimes1 = qDecreasing.top();
qDecreasing.pop();
int maxTimes2 = qDecreasing.top();
qDecreasing.pop();
// add up the times needed
maxTotalTimes += maxTimes1 + maxTimes2 - 1;
// push the merged sequence to the list
qDecreasing.push(maxTimes1 + maxTimes2);
}According to the Huffman algorithm, only a for-loop is needed. And the push() and pop() of priority_queue has a time complexity of \(log k\), where \(k\) is the number of sequences to be merged. Thus the time complexity is
\[
T(k) = O(k log k)
\]
And a queue, which is actually a heap, is needed to store the sequences. According to the Huffman algorithm the maximal length of the queue is \(k\). Thus the space complexity is
\[
S(k) = O(k)
\]
The greedy algorithm is a lot easier than DP. The key point is we should confirm that the global optima of the task can be found out using the greedy algorithm, with the two properties introduced above.
#include <iostream>
#include <queue>
using namespace std;
int main() {
/* receive inputs */
int k; // number of sequences to be merged
cin >> k;
// store sequences in a decreasing order
priority_queue<int> qDecreasing;
// store sequences in an increasing order
priority_queue<int, vector<int>, greater<> > qIncreasing;
// receive lengths of sequences
for (int i = 1; i <= k; i++) {
int input;
cin >> input;
qDecreasing.push(input);
qIncreasing.push(input);
}
/* greedy algorithm */
int minTotalTimes = 0;
int maxTotalTimes = 0;
for (int i = 1; i <= k - 1; i++) {
// find two shortest sequences
int minTimes1 = qIncreasing.top();
qIncreasing.pop();
int minTimes2 = qIncreasing.top();
qIncreasing.pop();
// add up the times needed
minTotalTimes += minTimes1 + minTimes2 - 1;
// push the merged sequence to the list
qIncreasing.push(minTimes1 + minTimes2);
// find two longest sequences
int maxTimes1 = qDecreasing.top();
qDecreasing.pop();
int maxTimes2 = qDecreasing.top();
qDecreasing.pop();
// add up the times needed
maxTotalTimes += maxTimes1 + maxTimes2 - 1;
// push the merged sequence to the list
qDecreasing.push(maxTimes1 + maxTimes2);
}
/* display */
cout << maxTotalTimes << " " << minTotalTimes;
return 0;
}references:
1. 优先队列priority_queue的比较函数
2. priority_queue用法详解
标签:get better tom because 收获 时间 therefore tor round
原文地址:https://www.cnblogs.com/Chunngai/p/11874215.html