标签:for 图片 can dfs 一个 情况 size 遍历 color
POJ 3585 Accumulation Degree 题解
题目的字面意思
给出了一个带权无向图,然后可以任意选一个点做源点,往里面倒水,问最终,可以从叶子节点中流出多少水

在了解题意之后, 基本就可以想到是赤裸裸的树形dp
先来考虑需要注意的问题
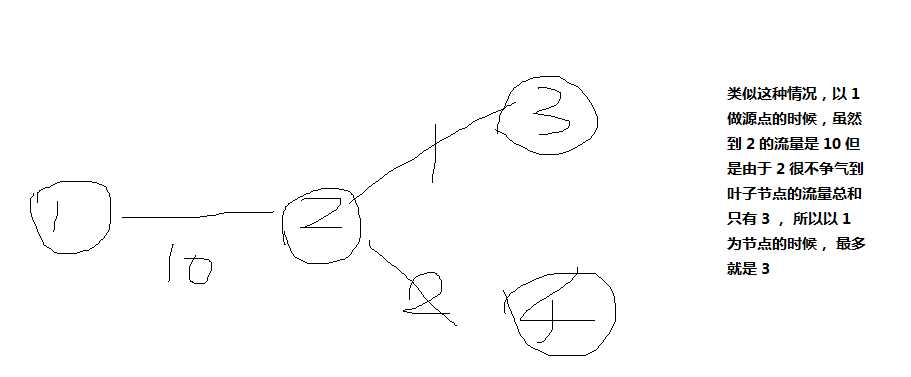
在弄清以上的概念之后,就可开始设计算法了
众所周知, 树形dp 是没法往上走的, 所以我们需要维护两个数组,一个down一个up (down 表示 该节点以dfs序往下走的最大叶子节点流量的和, up则表示往父节点的),最后只需要遍历每个节点的down和up 的和就可以了
转移方程(u 表示父节点 v 表示子节点 w 为当前边的权值)
Down[u] += min(w[i], down[v])
需要考虑,子节点够不够争气, 能不能承受那么w[i]多的流量
第一遍dfs 处理完down
Up[v] = min(w[i], up[u] + down[u] – min(w[i], down[v]));
需要考虑能不能往父节点流w[i]多的流量
up[u] + down[u] – min(w[i], down[v]) 这个是计算如果父节点不往当前子节点流, 最多可以流向叶子节点多少。
然后需要特殊处理子节点是叶子节点的情况, 就不要取最小值了, 一定可以流w[i] 那么多
第二遍dfs 处理up
Talk is cheap, I will show you my code
#include <stdio.h> #include <algorithm> #include <cstring> using namespace std; const int N = 2e5+10; int head[N] = {0}, tot = 0, to[N*2], nt[N*2]; long long w[N*2]; void add(int a, int b, int c) { ++tot;to[tot]=b;nt[tot]=head[a];head[a]=tot;w[tot]=c; ++tot;to[tot]=a;nt[tot]=head[b];head[b]=tot;w[tot]=c; } long long res = 0; long long up[N], down[N]; void dfs1(int now, int pre) { for(int i = head[now]; i; i = nt[i]) { if(to[i]==pre) continue; dfs1(to[i], now); if(down[to[i]]==0) down[now] += w[i]; // 叶子节点情况 else down[now] += min(down[to[i]], w[i]); } } void dfs2(int now, int pre) { for(int i = head[now]; i; i = nt[i]) { if(to[i]==pre) continue; // 叶子节点情况 if(down[to[i]]==0) up[to[i]] = min(w[i], up[now] + down[now] - w[i]); else up[to[i]] = min(w[i], up[now] + down[now] - min(w[i], down[to[i]])); dfs2(to[i], now); } } int main() { int T, n, a, b, c; scanf("%d", &T); while(T--) { scanf("%d", &n); tot = 0; // 初始化 没有就是RE memset(head, 0, sizeof(head)); memset(up, 0, sizeof(up)); memset(down, 0, sizeof(down)); for(int i = 1; i < n; i++) { scanf("%d %d %d", &a, &b, &c); add(a, b, c); //自写邻接表建图 } dfs1(1, 0); dfs2(1, 0); res = 0; //遍历取个最大值 for(int i = 1; i <= n; i++) res = max(res, up[i] + down[i]); printf("%lld\n", res); } }
POJ 3585 Accumulation Degree 题解
标签:for 图片 can dfs 一个 情况 size 遍历 color
原文地址:https://www.cnblogs.com/loenvom/p/11876082.html