红黑树

标签：for   following   导致   bst   组合   span   geek   导出   应用   

红黑树第一部分：介绍

红黑树是一种自平衡的二叉搜索树(BST)，其中每个节点遵循以下规则。

• 每个节点都有红色或黑色
• 树的根总是黑色的
• 没有两个相邻的红色节点(红色节点不能有红色的父节点或红色的子节点)
• 从节点(包括根)到其任何子代NULL节点的每条路径都具有相同数量的黑色节点

为什么要用红黑树

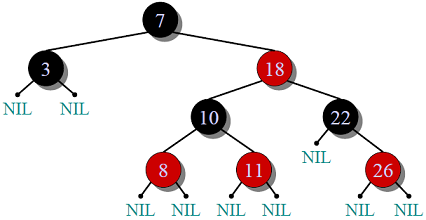
大多数BST操作(例如，搜索，最大，最小，插入，删除等)取\(O(H)\)时间，其中H是BST的高度。对于倾斜二叉树，这些操作的成本可以变为\(O(N)\)。如果我们确保在每次插入和删除后树的高度保持\(O(logN)\)，那么我们可以保证所有这些操作的上限为\(O(logN)\)。红黑树的高度始终为\(O(logN)\)，其中n是树中的节点数。

和AVL树作比较

与红黑树相比，AVL树更平衡，但它们在插入和删除期间可能会导致更多的旋转。因此，如果您的应用程序涉及许多频繁的插入和删除，那么红黑树应该是首选的。如果插入和删除的频率较低，并且搜索是更频繁的操作，则AVL树应该优先于红黑树。

红黑树如何确保平衡？

理解平衡的一个简单示例是，红黑树中不可能有3个节点的链。我们可以尝试任何颜色的组合，看它们是否违反了红黑树的属性。

A chain of 3 nodes is nodes is not possible in Red-Black Trees. 
Following are NOT Red-Black Trees
     30             30               30       
    / \            /  \             /     20  NIL      20(r)  NIL       20(r)  NIL
   / \             / \              /  \   
 10  NIL          10  NIL        10(r)  NIL  
违反性质 4        违反性质 4       违反性质 3
以下是不同的可能的红黑树，具有以上3个键
        20                           20
       /   \                        /         10     30                  10(r)   30(r)
     /  \   /  \                 /  \    /     NIL  NIL NIL NIL             NIL  NIL NIL NIL

从上面的例子中，我们了解到红黑树是如何确保平衡的。以下是红黑树平衡的一个重要事实。

• 红黑树的黑色高度：
  黑色高度Black Height是从根到叶的路径上的黑色节点数。叶节点也算作黑色节点。从上述性质3和4，我们可以推导出高度为h的红黑树具有 \(Black Height >= h/2\)。

红黑树

标签：for   following   导致   bst   组合   span   geek   导出   应用   

原文地址：https://www.cnblogs.com/wjundong/p/11888437.html