multivariate_normal 多元正态分布

标签：椭圆   code   ace   并且   pos   pytho   inf   sig   适用于   

多元正态分布

正态分布大家都非常熟悉了，多元正态分布就是多维数据的正态分布，其概率密度函数为

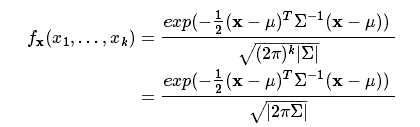
上式为 x 服从 k 元正态分布，x 为 k 维向量；|Σ| 代表协方差矩阵的行列式

二维正态分布概率密度函数为钟形曲面，等高线是椭圆线族，并且二维正态分布的两个边缘分布都是一维正态分布，如图

np.random.multivariate_normal

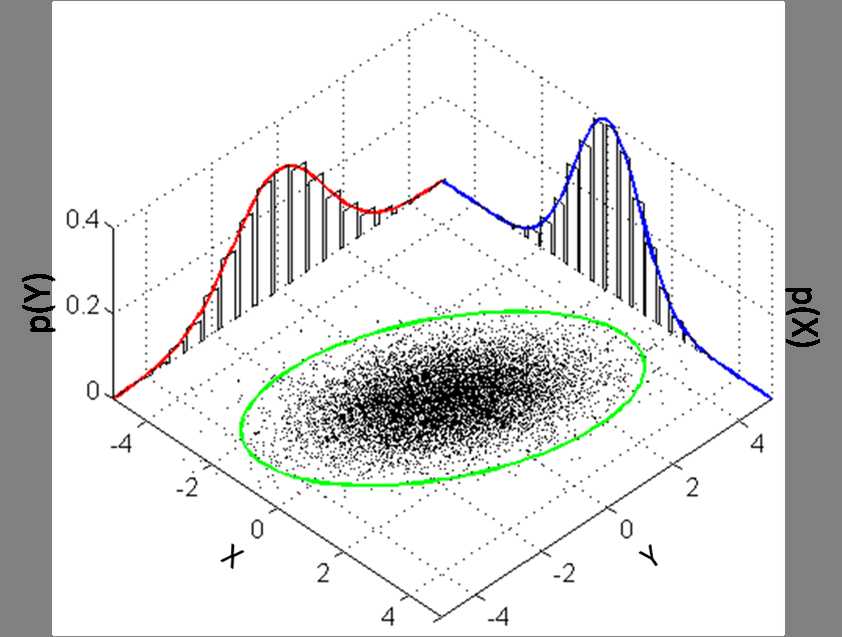
生成一个服从多元正态分布的数组　　　　　　【适用于 python3，但在 python2 中也能用】

multivariate_normal(mean, cov, size=None, check_valid=None, tol=None) 

mean：均值，维度为1，必选参数；

cov：协方差矩阵，必选参数；

size： 指定生成矩阵的维度，若size=(1, 1, 2)，则输出的矩阵的 shape 即形状为 1X1X2XN（N为mean的长度）；

check_valid：可取值 warn，raise以及ignore；

tol：检查协方差矩阵奇异值时的公差，float类型；

示例

mean = (1, 2)
cov = [[1, 0], [0, 1]]
x = np.random.multivariate_normal(mean, cov, (2, 2), ‘raise‘)   # 2x2x2
print(x)   

直接生成数组

scipy.stats.multivariate_normal

生成一个多元正态分布

def __call__(self, mean=None, cov=1, allow_singular=False, seed=None)

示例-生成多元正态分布

import numpy as np
import scipy.stats as st
import matplotlib.pylab as plt

x, y = np.mgrid[-1:1:.01, -1:1:.01]
pos = np.empty(x.shape + (2,))
pos[:, :, 0] = x; pos[:, :, 1] = y
rv = st.multivariate_normal([0, 0], [[1, 0], [0, 1]])   # 生成多元正态分布
print(rv)       # <scipy.stats._multivariate.multivariate_normal_frozen object at 0x08EDDDB0> 只是生成了一个对象，并没有生成数组
plt.contourf(x, y, rv.pdf(pos))
plt.show()

示例-概率密度函数

x = np.linspace(0, 5, 10, endpoint=False)       # 样本
y = st.multivariate_normal.pdf(x, mean=2.5, cov=.5)        # 样本的概率密度函数

plt.plot(x, y)
plt.show()

生成了概率密度曲线

可用方法

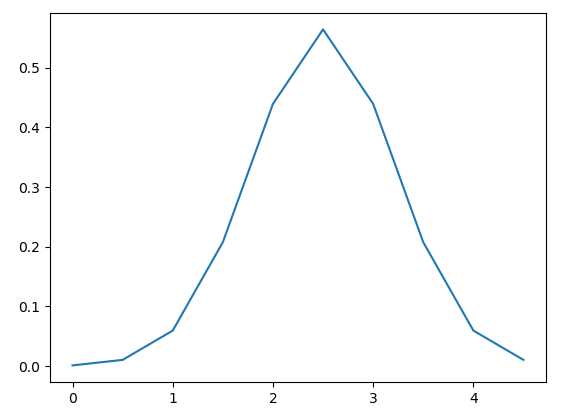
pdf(x, mean=None, cov=1) ：概率密度函数

logpdf(x, mean=None, cov=1) ：概率密度函数日志

rvs(mean=None, cov=1) ：从多元正态分布中随机抽取样本

entropy() ：计算多元法线的微分熵

参考资料：

https://www.cnblogs.com/21207-iHome/p/8039741.html　　多元正态分布

https://blog.csdn.net/zch1990s/article/details/80005940　　np.random.multivariate_normal方法浅析

https://www.cnblogs.com/wanghui-garcia/p/10763418.html 　　scipy.stats.multivariate_normal的使用

multivariate_normal 多元正态分布

标签：椭圆   code   ace   并且   pos   pytho   inf   sig   适用于   

原文地址：https://www.cnblogs.com/yanshw/p/11898408.html