标签:com block class 路径 左右子树 文件 mat math 图片
Huffman树又称为最优树,是一种带权路径最短的树。
在一棵树中我们把一个节点到另一个节点之间的通路叫做路径,在路径中每经过一个节点路径的长度就加一。如果对一个节点附上权值,则该节点的带权路径长为该节点到树根的路径长与权的乘积。
在一棵有\(n\)个叶子节点的树中,令每个叶子节点的权为\(w_i\),路径长为\(l_i\),则树的带权路径长\(WPL=\sum_{k=1}^{n}w_kl_k\)。
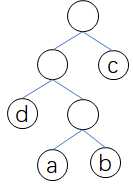
如图所示,令a、b、c、d分别带权7、5、2、4,这他们的带权路径长为\(WPL=7*3+5*3+2*1+4*2=46\)。
对一颗二叉树,如果对一组给定的权,使得其WPL最小,那么这颗二叉树称为Huffman树(或最优二叉树)。
Huffman树的构造方法:
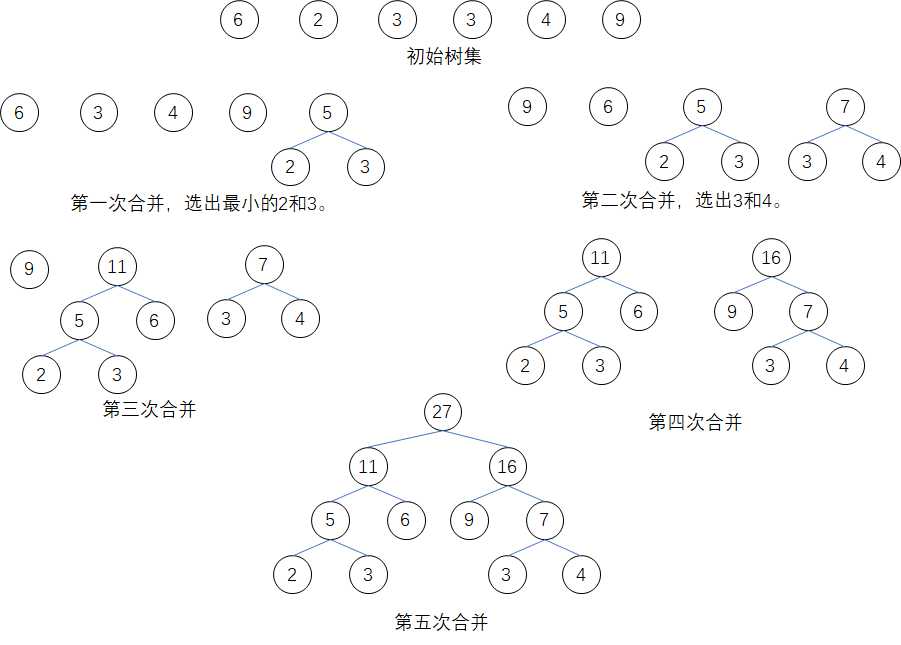
(1)首先建立一组二叉树集合,每颗二叉树仅含一个节点,每个节点对应一个权值。
(2)在二叉树集合中选取权值最小的两科二叉树,把它们合并为一颗新树,新树根节点的左右子树为所选的二叉树,新树的权值为两颗子树权值的和。
(3)在树集中删去选出的两颗二叉树,并将新树加入树集中。
(4)重复(2)和(3),直到树集中只剩下一颗二叉树,这棵树便是所需的Huffman树。
如图:
Huffman编码是一种编码方式,主要用于数据文件的压缩。Huffman编码是一种不定长度编码,它保证让经常使用的字符拥有较短的编码,来加快文件传输的效率。
假如我们有\(n\)个字符,且每个字符在文件里出现的频数为\(w_i(i=1,2,...,n)\)。则我们以\(n\)个字符作为初始树集,并以\(w_i\)作为对应的权值构建Huffman树,且约定左分支为字符‘0‘,右分支表示字符‘1‘,则从根节点到叶子节点的路径上分支字符所组成的字符串即为对应字符的Huffman编码。
假如我们有一个文件,它只包含字符‘a‘,‘s‘,‘d‘,‘f‘,‘g‘,并且字符对应出现的频数为12,4,8,15,9,以此为基础建立Huffman树如下图所示:
标签:com block class 路径 左右子树 文件 mat math 图片
原文地址:https://www.cnblogs.com/sigmun/p/11785996.html