标签:保存 info 存储结构 不同 删除 section 磁盘性能 严格 读取
[TOC]
在说B树之前最好先看看2-3树, 2-3树是B树的一种特例, 什么B树, B树就是2-3树, 2-3-4 树 , 2-3-4-5... 树的统称, 而B+树又是B树的一种变形
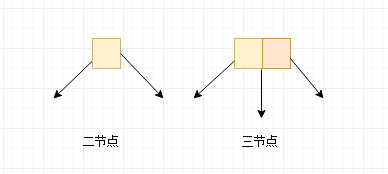
像上图那样,可以有两个子节点的节点叫做二节点, 可以有三个子节点的节点叫做三节点, 并且, 对于二节点来说,可以有节点,也可以,没有节点, 同样对三节点来说,要么有三个节点要么有没节点, 只有这两种情况(不能只有一个节点)
如果一棵树中最大的节点数为m, 我们就称它是m阶的B树
注意点就是B树的所有的子节点全部在同一层, 如果不在同一层了,它肯定不是B树,下文中会讲解调整的技巧
特性:
假设每一个节点能存储的元素的个数为x
? 对于根节点来说: 根节点能存储的元素的范围是 1<= x ? m-1 (m为阶数)
? 对于非根节点来说: 他能存储的元素的个数是 ?? m/2 ? -1 ? x ? m-1
像下面这样, 如果当前节点有子节点的话, 子节点的个数是当前节点中存储的元素数+1
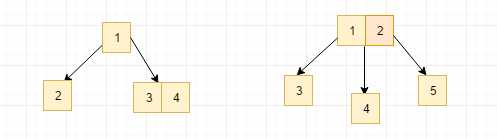
推论:
如果当前节点是根节点, 那么, 当前节点的子节点的个数为x: 2 ? x ? m
如果当前节点是非根节点, 那么, 当前节点的子节点的个数x : ?? m/2 ? ? x ? m
**例子: **
比如当m=3时, 也就是说,当前树为3阶B树, 通过上面的公式计算它的非根节点的个数是 ? m/2 ? ? x ? 3 即 [2,3] , 此时这棵树就是我们所说的2-3树
假设我们有这样一个数组: [6,10,4,14,5,11,15,3,2,12,1,7,8] 下面通过画图将它转换成一个3阶B树
在转化的过程中, 严格遵循上面的特性:
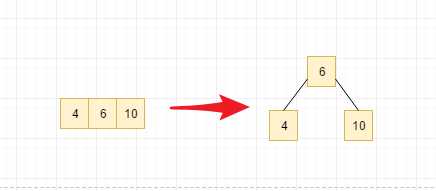
先添加node6, 对于二三树来说,最多的节点数是三节点的状态, 于是我们继续添加node10, 得到的下图

因为node4比node6小, 所以我们想把node4添加到node6的左边, 但是此时4,6,10, 三个节点排放在一起就是4节点,不满足2-3的要求,所以我们需要进行上溢调整 , (或者说,当一个节点中存储的元素的个数=m时, 进行上溢处理)
第一步: 先求出需要上溢的节点的中间元素的位置 k (就是下面node6的位置2)
第二步: 将k位置的元素向上移动和父节点合并, 没有父节点,就让他当父节点
第三步: 将[0-k-1] 和 [k-1,m-1] 位置的元素分裂成上溢节点的左右节点
每次上到父节点时,就会导致树长高, 还需要注意的地方就是上溢可能会导致当前节点的父节点满了, 这时候重复这个过程,对其父节点进行上溢的操作
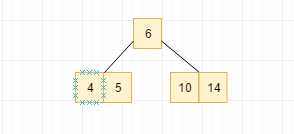
继续添加node5,和node14, 同样可以直接添加进去,且不会打破2-3的平衡
继续添加node11, 按照正常的排序,我们会将他排在node10的右边,但是此时同样,一个节点中三个元素,说明这个节点是4节点, 不符合2-3的三节点特性, 因此需要上溢, 同样是选出中间位置的11,然后和它的上一个父节点进行合并, 剩下的node10, node14当成这个node11的左右子节点

继续添加node15, 按照大小,我们将他排放在node14的右边,且满足二三树的要求
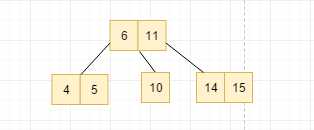
继续添加node3, 按照顺序应该将node3放在node4的左边,但是这个节点里面就回显345三个元素, 也就是说这个节点其实是4节点,因此我们将node4上溢, 和它的父节点合并, 然后我们又发现, 上溢到根节点中,根节点就有了三个元素, 因此我们进行继续上溢, 于是树就会长高一层

继续我们插入node2, 按照大小它被放在node3的左边, 同时树也不会被打破平衡
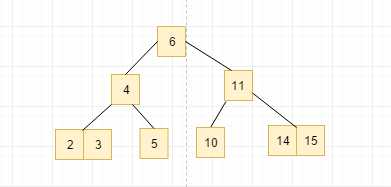
接着我们插入node12, 同样按照顺序它应该被插入在node14的左边, 但是此时,这个节点中又出现了三个元素, 又出现了4节点, 我们重新进行上溢出, 同样是找到 12 14 15 中间的14去和父节点node11进行合并,下图
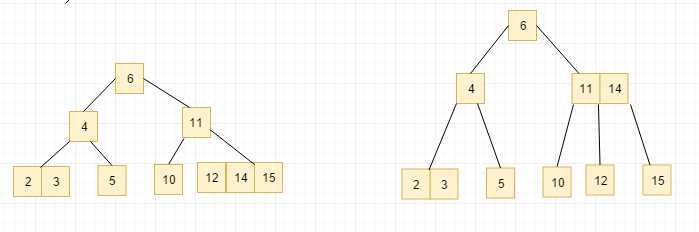
用和上面相反的过程我们可以插入node1
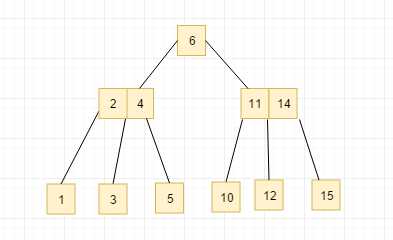
同样插入s10这个节点, 同样我们会发现7,8,10三个元素在同一个节点上, 因此我们需要上溢, 然后8,11,14又在同一个节点上, 继续进行上溢, 然后得到下图
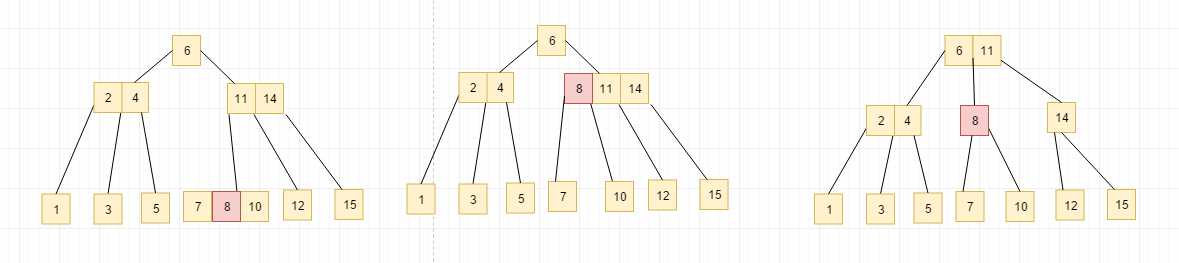
删除一个节点:
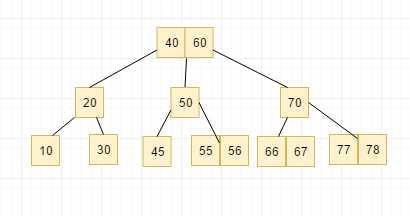
比如我们想删除60这个节点
于是我们找到node60的前驱节点, 怎么找呢? 从node60开始,往左走一次, 然后往右走到头
如果我们想找到node60的后继节点怎么找呢? 从node60开始,往右走一步,然后往左走到头
underflow下溢
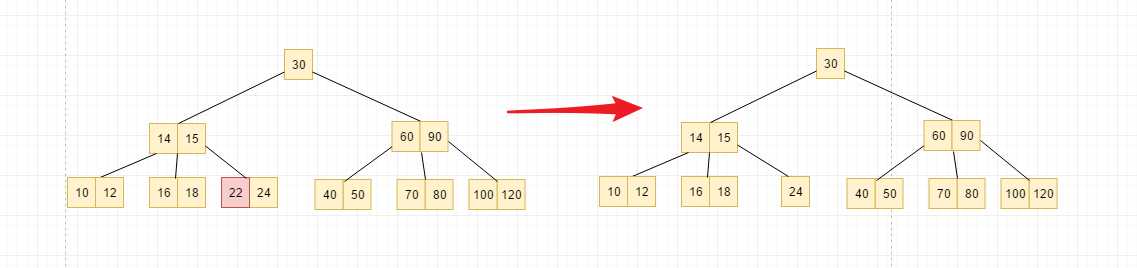
上溢的话,就是节点会往上走,下溢正好是相反的过程, 比如说,上树m=5, 即5阶的B树, 我们想删除上面的node22, 但是node22被删除后,就只剩下了node24, 这时候就违背了B树的定义, 每一个节点中至少要有 ? m/2 ? -1个元素,即 ? 5/2 ? -1 = 2 个元素
下溢节点中元素的数量必定是 ? 5/2 ? -2
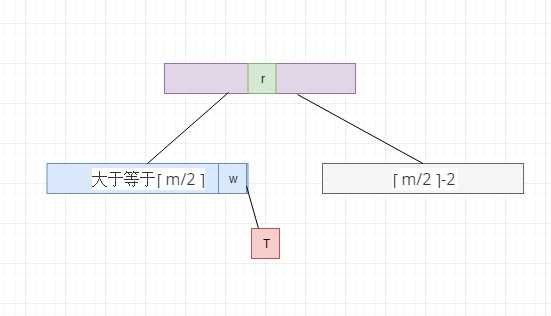
我们在删除了根节点的右子树中的元素,直接导致了这个节点中的元素个数为 ? m/2 ? -2 , 但是B树中要求的是至少为 ? m/2 ? -1 , 我们就向它的兄弟节点借元素, 因为它的兄弟节点的元素个数比 最低要求还大1, 于是向下面这样变动,让根节点中间的元素,放到根节点右子节点的最左边, 根节点左节点的最右侧的元素放到根节点的中间位置, (注意为了不打破树的平衡,我们需要讲nodeT也倒换过去)
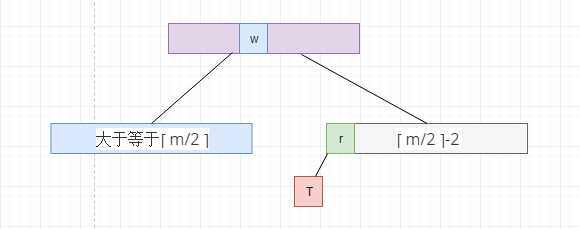
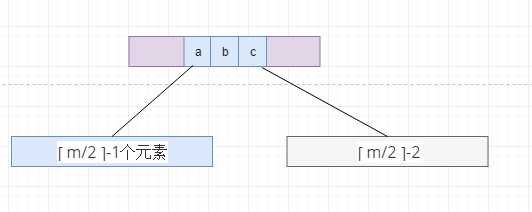
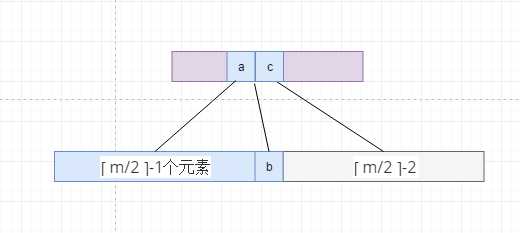
进行元素的合并, 像下面这样,需要注意的地方就是此时父节点的元素中个数可能不足够 ? m/2 ? -1,因此我们重复这个过程
B树又称为多路搜索树, 是为不同的存储设备设计的平衡查找树,
前面一片博文中我们知道, AVL树确实能中和链式存储结构和顺序存储结果的优缺点, 在添加和删除方面都能表现出优越的性能,这里我们 可以将B树理解成是平衡二叉树的升级版
B树不一定只有两个叉, 但是B树和二叉平衡树一样都是有序的, 即当我们按照中序遍历它树, 可以得到有序数列, 而且B树比AVL树更胖,更矮, ,因此树越高, IO次数就会越大,但是也带来了更多的优势, 每次在磁盘上读取数据时,都会进行一次预读, 使用B树可以很好的实现这个特性
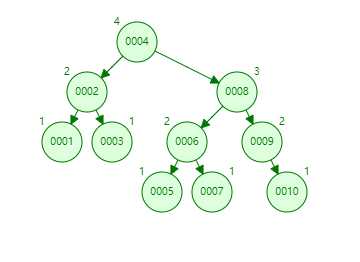
假设使用AVL树建立索引, 如上图, 索引文件不会被保存在内存中, (避免索引文件过大,导致内存的溢出), 于是我们如果想根据索引读取数据, 瓶颈就在每次读取索引文件和磁盘之间的IO上
假设我们有上面的树, 然后我们查询node10, 会和磁盘进行如下几次IO
第一次与磁盘的IO : 读取node4, 往右走
第二次与磁盘的IO : 读取node8, 往右走
第三次与磁盘的IO : 读取node9, 往右走
第四次与磁盘的IO : 定位 node10, 结束
虽然使用AVL树建立索引并不是最好的选择, 但是和全表扫描,进行10次IO相比, 效率还是很明显的高效
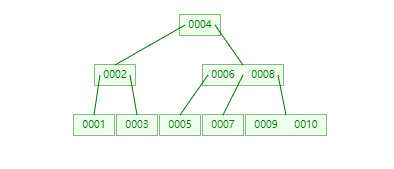
同样我们想查询node10
第一次与磁盘的IO : 读取node4, 往右走
第二次与磁盘的IO : 读取node6,node8, 往右走
第三次与磁盘的IO : 读取node9,定位到node10
很明显,B树会比AVl树更矮, 当存储的数据超级庞大时, 它甚至可以比AVL树减少一半的IO次数
同样, B树的范围查询效率比较低
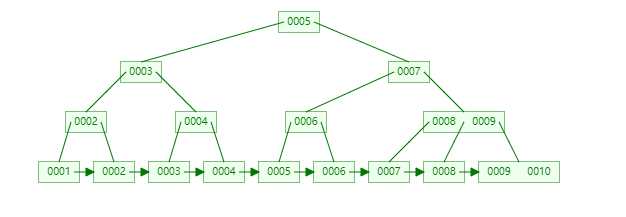
**概念: ** 在上树中, 只有最后一行叫做非叶子节点, 其他的都叫做叶子节点
B+树,是B树的一种变体,查询性能更好。
m阶的B+树的特征:
B+树相比于B树的查询优势:
缺点: 会用冗余的节点, 比较占硬盘的大小, (但是这些冗余的节点都是索引,会大大提高查询速度)
标签:保存 info 存储结构 不同 删除 section 磁盘性能 严格 读取
原文地址:https://www.cnblogs.com/ZhuChangwu/p/11905005.html