每日一题_191122

标签：ant   code   inline   splay   图片   center   因此   rac   面积   

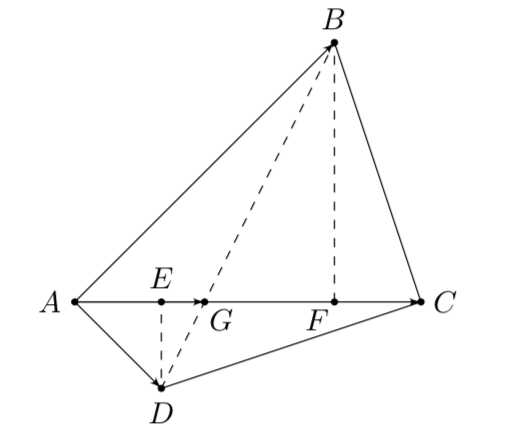
在平面四边形 \(ABCD\) 中,已知 \(\triangle ABC\) 的面积是 \(\triangle ACD\) 的面积的 \(3\) 倍,若存在正实数 \(x,y\),使得 \(\overrightarrow{AC}=\left(\dfrac{1}{x}-3\right)\overrightarrow{AB}+\left(1-\dfrac{1}{y}\right)\overrightarrow{AD}\) 成立,则\(x+y\)的最小值为\(\underline{\qquad\qquad}\).
解析:
如图,连接\(BD\)交\(AC\)于点\(G\),分别过\(B,D\)作\(AC\)的垂线,

每日一题_191122

标签：ant   code   inline   splay   图片   center   因此   rac   面积   

原文地址：https://www.cnblogs.com/Math521/p/11906375.html