标签:style blog http io color os ar for sp
一开始题意没读懂 = =
题意:比如说对于表盘上a到b、c到d都要连边,这两个边不能交叉。这两个边要么都在圆内要么都在圆外,而且可以是曲线= =
比如这种情况:(Reference:http://blog.csdn.net/l04205613/article/details/6668318)
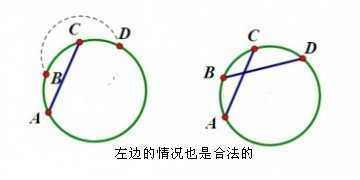
(左边情况看似是合法的,但是一个边在圆内一个在圆外,形成矛盾了)
这回只需判断是否可行不用输出方案,这样就简单多了
STEP:构图,矛盾的地方连边->tarjan求scc->判断是否a和not a在同一分量内

1 #include "iostream" 2 #include "cstring" 3 #include "stack" 4 using namespace std; 5 #define maxn 2010 6 7 int G[maxn][maxn],dx[maxn],dy[maxn]; 8 int pre[maxn],lowlink[maxn],sccno[maxn]; 9 int dfs_clock,scc_cnt,N,M; 10 stack<int> St; 11 12 void tarjan(int u) 13 { 14 pre[u]=lowlink[u]=++dfs_clock; 15 St.push(u); 16 for (int i=1;i<=G[u][0];i++) 17 { 18 int v=G[u][i]; 19 if (!pre[v]) 20 { 21 tarjan(v); 22 lowlink[u]=min(lowlink[u],lowlink[v]); 23 } 24 else if (!sccno[v]) 25 { 26 lowlink[u]=min(lowlink[u],pre[v]); 27 } 28 } 29 if (lowlink[u]==pre[u]) 30 { 31 scc_cnt++; 32 for (;;) 33 { 34 int x=St.top(); 35 St.pop(); 36 sccno[x]=scc_cnt; 37 if (x==u) break; 38 } 39 } 40 } 41 42 void find_scc(int n) 43 { 44 dfs_clock=scc_cnt=0; 45 memset(sccno,0,sizeof(sccno)); 46 memset(pre,0,sizeof(pre)); 47 for (int i=1;i<=n;i++) 48 if (!pre[i]) 49 tarjan(i); 50 } 51 52 void add_edge(int x,int y) 53 { 54 G[x][0]++; 55 G[x][G[x][0]]=y; 56 } 57 58 int main() 59 { 60 cin>>N>>M; 61 for (int i=1;i<=M;i++) 62 cin>>dx[i]>>dy[i]; 63 64 //1->N:dx[i]->dy[i]走圆内 65 //N+1->2*N:dx[i]->dy[i]走圆外 66 for (int i=1;i<=N;i++) 67 { 68 for (int j=i+1;j<=N;j++) 69 { 70 if ((dx[j]<dx[i])&&(dx[i]<dy[j])&&(dy[j]<dy[i])) 71 { 72 add_edge(i,j+N); 73 add_edge(j+N,i); 74 add_edge(j,i+N); 75 add_edge(i+N,j); 76 } 77 if ((dx[i]<dx[j])&&(dx[j]<dy[i])&&(dy[i]<dy[j])) 78 { 79 add_edge(i,j+N); 80 add_edge(j+N,i); 81 add_edge(j,i+N); 82 add_edge(i+N,j); 83 } 84 } 85 } 86 87 find_scc(2*N); 88 89 for (int i=1;i<=N;i++) 90 { 91 if (sccno[i]==sccno[i+N]) 92 { 93 cout<<"the evil panda is lying again"<<endl; 94 return 0; 95 } 96 } 97 cout<<"panda is telling the truth..."<<endl; 98 return 0; 99 100 }
------------------------------------------------------------------------------------------------
注意:对于2-SAT问题构图的时候有些题还要纠结一下是连单向边(如poj3678)还是双向边(如本题),
reference:http://blog.csdn.net/u011026968/article/details/10823853
本题中,我们以第二个判断条件if ((dx[i]<dx[j])&&(dx[j]<dy[i])&&(dy[i]<dy[j]))为例:
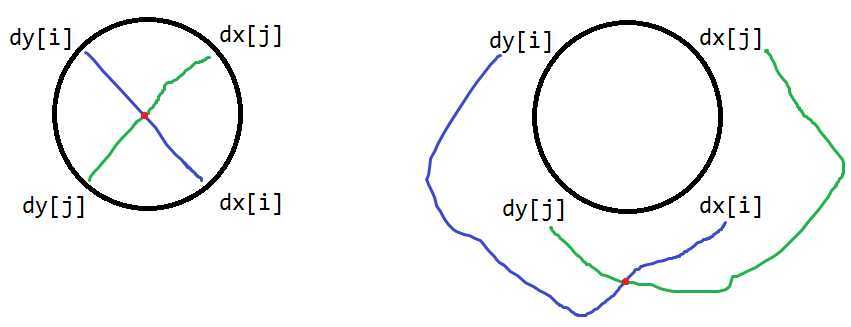
若j在圆内,那么i一定在圆外
若j在圆外,那么i一定在圆内
若i在圆内,那么j一定在圆外
若i在圆外,那么j一定在圆内
注意蓝色部分就是双向边了
------------------------------------
而poj 3683题中:
我们以构图时的第一个判断条件if (min(S[i]+D[i],S[j]+D[j])>max(S[i],S[j]))为例,
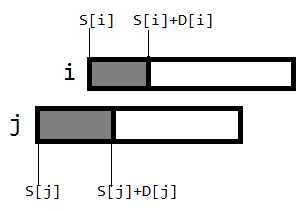
若i在前段举行,那么j一定在后半段举行
若j在后半段举行,那么i不一定要在前半段举行
若j在前段举行,那么i一定在后半段举行
若i在后半段举行,那么j不一定要在前半段举行
注意红色部分:因为不确定(本判断条件中并没有讨论后半段的时间),所以不能双向边
标签:style blog http io color os ar for sp
原文地址:http://www.cnblogs.com/pdev/p/4060698.html