DFT与傅里叶变换的理解

根据信号的不同类型，可以把傅立叶变换分为四类：

1) 非周期性连续信号： 傅立叶变换(Fourier Transform，FT)

2) 周期性连续信号： 傅立叶级数(Fourier Series，FS)

3) 非周期性离散信号： 离散时域傅立叶变换(Discrete Time Fourier Transform ,DTFT)

4)周期性离散信号： 离散傅立叶变换(Discrete Fourier Series，DFS)

根据时域与频域的对应关系，我们可以知道，周期<---->离散，是一对对偶关系，即周期信号的傅里叶变换一定是离散的，离散信号的傅里叶变换一定是周期的，反之也成立。

所以针对上述四种傅里叶变换，我们知道，FT的结果具有连续非周期性质，FS的结果具有离散非周期性质，DTFT结果具有连续周期性质，DFT结果具有离散周期性质。

非周期连续信号的傅里叶变换(FT)为：

非周期离散序列的傅里叶变换(DTFT)为：

周期连续信号的傅里叶变换(FS)为：

周期离散信号的傅里叶变换(DFS)为：

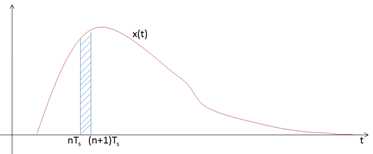
假定x(n)为T_s区域上x(t)的均值，且T_s（抽样间隔）足够小，如下图所示：

则有

其中

所以非周期连续信号与非周期离散信号之间频谱关系为：

F_FT(ω)=T_s·F_DTFT(ω) （ω<2πf_s）

同样可以推导周期连续信号与周期离散信号之间频谱关系为：

F_FS(ω_k)=T_s/T·F_DFS(ω_k)=1/N·F_DFS(ω_k) （k<N）

上述等式所加的限定是由于离散信号的频谱具有周期性，等价于原连续信号频谱以f_s为周期进行平移。这是由于离散信号的傅里叶变换的核函数具有周期性,例如DTFT的核函数为e−iωnTse−iωnTs，当ω增加2πf_s时，其值仍然不变。

假若连续信号为一个波包，最高频率为f_H,只在有限时间内幅值不为0，则连续信号按周期T延拓后周期信号的傅里叶级数是原连续信号的频域抽样，抽样周期为1/T，其中T为周期信号的周期。公式表示为：

F_FS(ω_k)=1/T·F_FT(ω=ω_k)

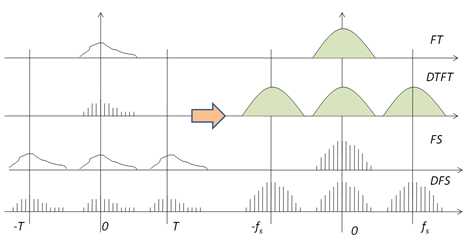
上述四种傅里叶变换的关系由下图可以对比看出：

上图中，离散信号的采样周期f_s>2f_H；FS变换的频谱分辨率为1/T.

在实际使用用计算机处理数据时，要求数据都是有限长度，而上述四种傅立叶变换都是针对无穷长度的信号。

针对有限长度的离散信号，定义了DFT：设x(n)是一个长度为N的有限长序列，则定义x(n)的N点离散傅里叶变换为：

其中W_N=exp(-j2π/N).

*matlab FFT函数中的W_N的定义与此不一样，与上式中的W_N成共轭关系，所以信号做fft之后需要使用fftshift函数变换后才与上式定义一致，这可从help和sin(2π/16*[0:127])的fft结果可以看出。

从DFT的定义式可以看出：

1）DFT可以视为非周期连续信号的FT在频域的抽样，值为F_DFT(ω_k) =f_s·F_FT(ω=ω_k)；

2）DFT也可以视为非周期离散信号的DTFT在主周期的抽样，值为F_DFT(ω_k) =F_DTFT(ω_k)；

3）DFT也可以视为周期连续信号FS，值为F_DFT(ω_k) =N·F_FS(ω_k)；

4）DFT也可以视为周期离散信号的DFS，但只取DFS的主周期，值为F_DFT(ω_k) =F_DFS(ω_k)。

对于上述四种信号的频谱密度，又有：

1）非周期连续信号的FT即为频谱密度；

2）非周期离散信号的频谱密度为F_FT(ω)=T_s·F_DTFT(ω) =F_DTFT(ω)/f_s

3）周期信号的频谱密度为FFT(ω)=2π∑k=−∞∞FFS(ωk)δ(ω−ωk)FFT(ω)=2π∑k=−∞∞FFS(ωk)δ(ω−ωk)，即在某些频点上，频谱密度无穷大；

4）周期离散信号频谱密度与周期连续信号类似，值为2πN∑k=−∞∞FDFS(ωk)δ(ω−ωk)2πN∑k=−∞∞FDFS(ωk)δ(ω−ωk)。

所以用DFT值得到相应信号的频谱密度，根据上述等式转换即可。如对于非周期连续信号的功率谱密度有：

问题：1）上述几个个等式与Paseval定理∫f(t)2dt=12π∫F(ω)2dω∫f(t)2dt=12π∫F(ω)2dω的关系？

            2）各个变换的量纲是什么？

DFT与傅里叶变换的理解

标签：rac   level   之间   over   orm   区域   tla   order   for   

原文地址：https://www.cnblogs.com/focus-z/p/11923532.html