标签：basic   Plan   原因   光照   ilo   dir   www   sphere   over   

C++实现光线追踪之详解

[参考文章]http://www.cnblogs.com/miloyip/archive/2010/03/29/1698953.html

1. 本文简介

作者正大三，刚好选修到计算机图形学这门课，基于兴趣，便试着实现全局光照的效果，由此，写下此篇文章。

2. 光线追踪

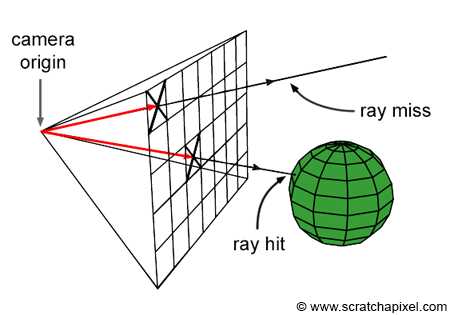
所谓光线追踪，是指从眼睛出发，经过图像平面每一像素，投射光线到场景中，求该光线与场景中几何图形的最近交点，然后求该交点的颜色属性，并将该颜色值记录下来，再根据相交点的材质判断性地进行反射、折射等现象继续追踪计算，最终把多次追踪交点颜色值的结果混合得到最终该像素的颜色值。（本文皆是介绍反向追踪）

• 图片来源: https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-overview/ray-tracing-rendering-technique-overview

  3. 场景说明

  4.1 摄像机
  此次实验，本人将摄像机放置于世界坐标系下的Vec3(0,5,15)下，图像平面置于Vec3(0,0,-1)处。注，为了简化，直接将图像设置width，height一致，均为600。
  
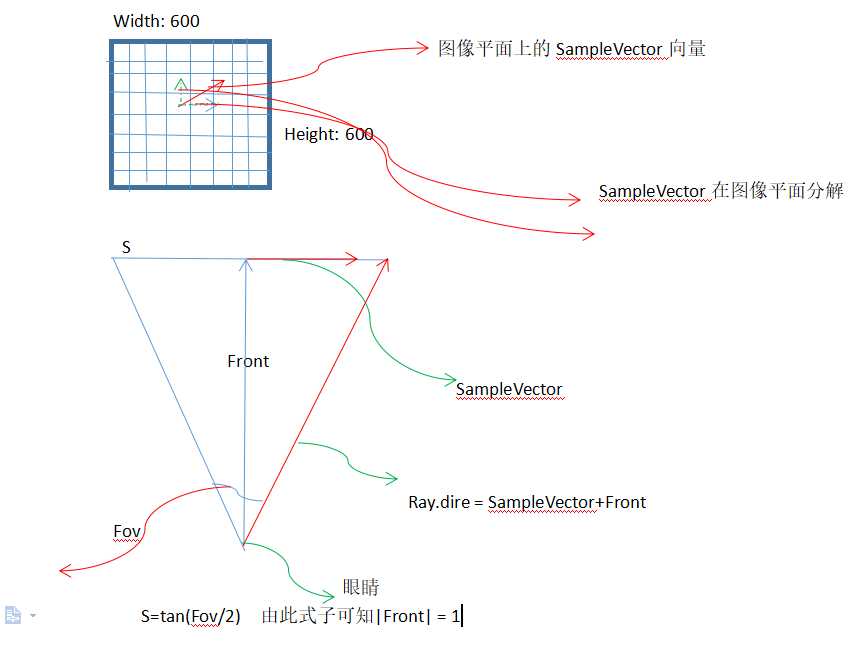
  图一
  特别注意：\(|front| = 1\)
  4.2 场景
  本实验中，场景由两个球以及一个无限平面组成。
  Sphere1：
  Sphere(Vec3(-10,10,-10),float(10))
  参数一:球心
  参数二：球径
  Sphere2:
  Sphere(Vec3(-10,10,-10),float(10))
  Plane:
  在数学表达上，无限平面可表示为\(nP=d\)，其中n为平面法向量，d为原点到平面的最短距离。
  Plane(Vec3(0,1,0),float(0))
  4.3 图像中坐标的转换
  最初，图像是600*600的平面，左上角为原点。现先转换为以左下角为原点的[0,1]范围内的平面。
  左上角为原点且范围为[0,600]：
  \(X = X\)...(1)
  \(Y = Y\)...(2)
  左下角为原点且范围为[0,1]：
  \(X = X/width\)...(2)
  \(Y = 1-Y/height\)...(2)
  图像中心为原点且范围为[-1,1]：
  \(X = 2X-1\)...(3)
  \(Y=2Y-1\)...(3)

4. 过程详解

(1)对于图像平面，自左向右，自上而下的经过每一像素投射光线
(2)计算光线与场景中几何图形的最近交点，都无交点即直接返回黑色，进行(5)，否则进(3)
(3)取样 即计算最近交点的颜色属性
(4)计算反射光线继续追踪，回到(2)。
(5)赋像素予颜色值，回到(1)

4.1 步骤一之生成光线
由图一可知，
\(Ray.dire = SampleVector+front\)...(4)
\(SampleVector=Vec3(X,Y,0)\)...(5)[注:此时是以中心为原点了]
即可得到初始化的Ray对象Ray(eye.origin,Ray.dire);

转换为中心为原点计算光线原因如下：
4.2 步骤二之计算最近交点

• 光线
  \(R(t)=eye.origin+tD\)（t为参数）
• 平面
  \(nP=d\)
  1）判断光线与法向量n是否垂直
  2）不垂直即可计算交点
  光线与无限平面的法向量位置情况：
  
  由上图可知，当\(n·Ray.dire>=0\)时，没有交点；否则，有交点。
  3）交点的计算：
  \(D=(d-eys.origin·n)/(t·n)\)
  
• 球
  

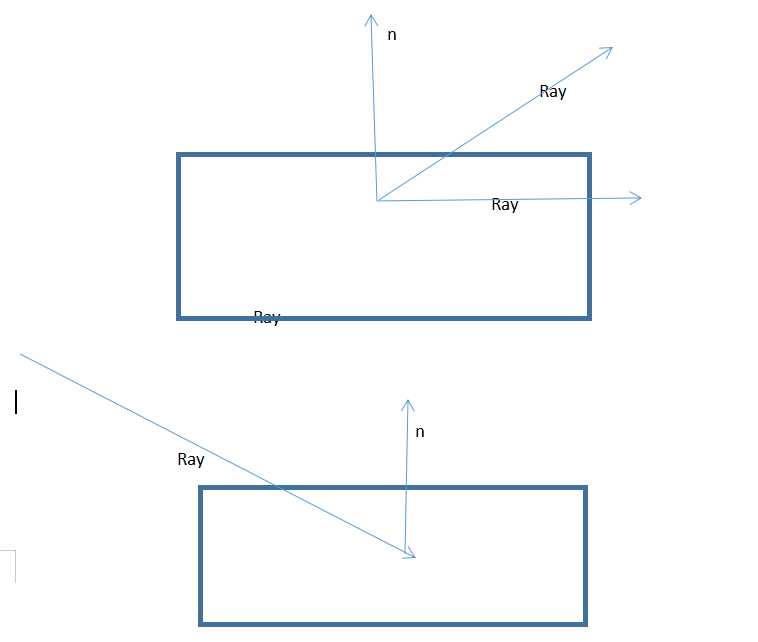
  推导过程复杂，作者不在此详细阐述，有兴趣的朋友可去这里查看

实现光线追踪

标签：basic   Plan   原因   光照   ilo   dir   www   sphere   over   

原文地址：https://www.cnblogs.com/LeeQMoon/p/11927538.html