标签:ali mat alt 文件的 网络流24题 max iostream height com
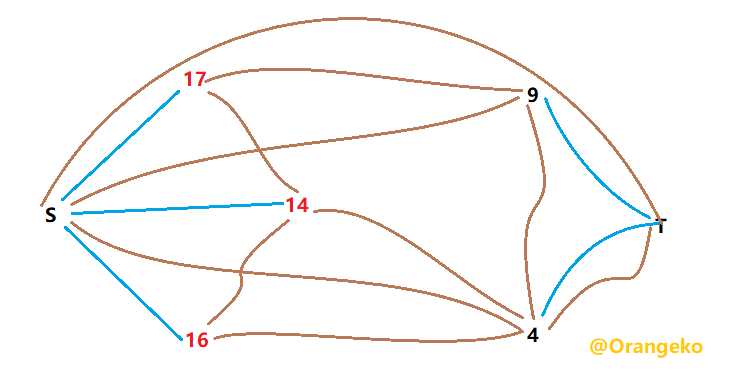
G 公司有 n 个沿铁路运输线环形排列的仓库,每个仓库存储的货物数量不等。如何用最少搬运量可以使 n 个仓库的库存数量相同。搬运货物时,只能在相邻的仓库之间搬运。
文件的第 1 行中有 1 个正整数 n,表示有 n 个仓库。
第 2 行中有 n 个正整数,表示 n 个仓库的库存量。
输出最少搬运量。
5
17 9 14 16 4
11
1≤n≤1001 \leq n \leq 1001≤n≤100
思路:建立超级源和超级汇,∵平衡时每个仓库的容量都是(Σa[i] )/ n,所以a[i] > avy的仓库,让它流向超级汇,以便过剩的流量能流出,a[i] < avy的仓库,让它连向超级源,使过剩的流量能流入。
对每个仓库之间连一条容量+OO的,花费为1的边,跑最小费用最大流
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;
const int maxn = 1e5 +7;
const int inf = 0x3f3f3f3f;
int n, m, s, t;
int head[maxn],pre[maxn],inq[maxn],dis[maxn];
int a[maxn];
int cnt = 1;
struct edge {
int u,to,nxt,w,c;
}e[maxn << 1];
template<class T>inline void read(T &res)
{
char c;T flag=1;
while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1;res=c-‘0‘;
while((c=getchar())>=‘0‘&&c<=‘9‘)res=res*10+c-‘0‘;res*=flag;
}
inline void BuildGraph(int u, int v, int w, int cost)
{
e[++cnt] = (edge){u, v, head[u], w, cost}, head[u] = cnt;
e[++cnt] = (edge){v, u, head[v], 0, -cost}, head[v] = cnt;///反向边
}
queue < int > q;
bool SPFA(int x)
{
memset(inq, 0, sizeof(inq));
for(int i = s; i <= t; i++) {
dis[i] = inf;
}
q.push(x);
dis[x] = 0;
inq[x] = 1;
while(!q.empty()) {
int u = q.front();
q.pop();
inq[u] = 0;
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to, w = e[i].c;
if(e[i].w) {
if(dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
pre[v] = i;
if(!inq[v]) {
q.push(v);
inq[v] = 1;
}
}
}
}
}
if(dis[t] == inf)
return 0;
return 1;
}
int MCMF()
{
int ans = 0;
while(SPFA(s)) {
int temp = inf;
for(int i = pre[t]; i; i = pre[e[i].u]) {
temp = min(temp, e[i].w);
}
for(int i = pre[t]; i; i = pre[e[i].u]) {
e[i].w -= temp;
e[i^1].w += temp;
ans += e[i].c * temp;
//printf("ans:%d\n",ans);
}
}
return ans;
}
int main()
{
read(n);
int sum = 0;
for(int i = 1; i <= n; i++) {
read(a[i]);
sum += a[i];
}
sum /= n;
s = 0; t = 2*n + 1;
for(int i = 1; i <= n; i++) {
if(sum > a[i]) {
BuildGraph(s, i, sum - a[i], 0);
}
if(sum < a[i]) {
BuildGraph(i, t, a[i] - sum, 0);
}
}
for(int i = 1; i <= n; i++) {
if(i == 1) {
BuildGraph(i, n, inf, 1);
BuildGraph(i, 2, inf, 1);
}
else if(i == n) {
BuildGraph(n, 1, inf, 1);
BuildGraph(n, n-1, inf, 1);
}
else {
BuildGraph(i, i+1, inf, 1);
BuildGraph(i, i-1, inf, 1);
}
}
printf("%d\n",MCMF());
return 0;
}
标签:ali mat alt 文件的 网络流24题 max iostream height com
原文地址:https://www.cnblogs.com/orangeko/p/11934619.html