标签:获得 深度学习 超出 最小二乘法 过程 数据 形式 图片 mic
相关问题:
1.弄清除为什么有这个东西,线性回归有什么不足,延申出了逻辑回归,线性回归为什么会不足以解决问题。
2.逻辑回归能怎么解决问题。自己能说出什么一般的例子,解决这些问题的推导过程是什么?
3.用到什么数学工具来构造逻辑回归的损失函数,为什么要选择这样的损失函数形式?
4.怎么样最终解决这个损失函数的最优化过程
5.逻辑回归的优缺点
问题1:线性回归可以预测连续值,但是不能解决分类问题,我们需要根据预测的结果判定其属于正类还是负类。
所以逻辑回归就是将线性回归的(−∞,+∞)结果,通过sigmoid函数映射到(0,1) 之间。
为什么使用sigmoid函数:
① 可以对(−∞,+∞)结果,映射到(0,1) 之间,作为概率。
② x<0,sigmoid(x)<0.5;x>0,sigmoid(x)>0.5 ; 可以将0.5作为决策边界。
③ 数学特性好,求导容易:g′(z)=g(z)⋅(1−g(z))
线性回归的损失函数为平方损失函数,如果将其用于逻辑回归的损失函数,则其数学特性不好,有很多局部极小值,
难以用梯度下降法求最优。
逻辑回归损失函数:对数损失函数

如果一个样本为正样本,那么我们希望将其预测为正样本的概率p越大越好,也就是决策函数的值越大越好,
则logp越大越好,逻辑回归的决策函数值就是样本为正的概率;
如果一个样本为负样本,那么我们希望将其预测为负样本的概率越大越好,也就是(1-p)越大越好,即log(1-p)越大越好。
为什么要用log:
样本集中有很多样本,要求其概率连乘,概率为(0,1)间的数,连乘越来越小,利用log变换将其变为连加,不会溢出,不会超出计算精度。
逻辑回归模型是非线性模型,不能用通常的最小二乘法来估计
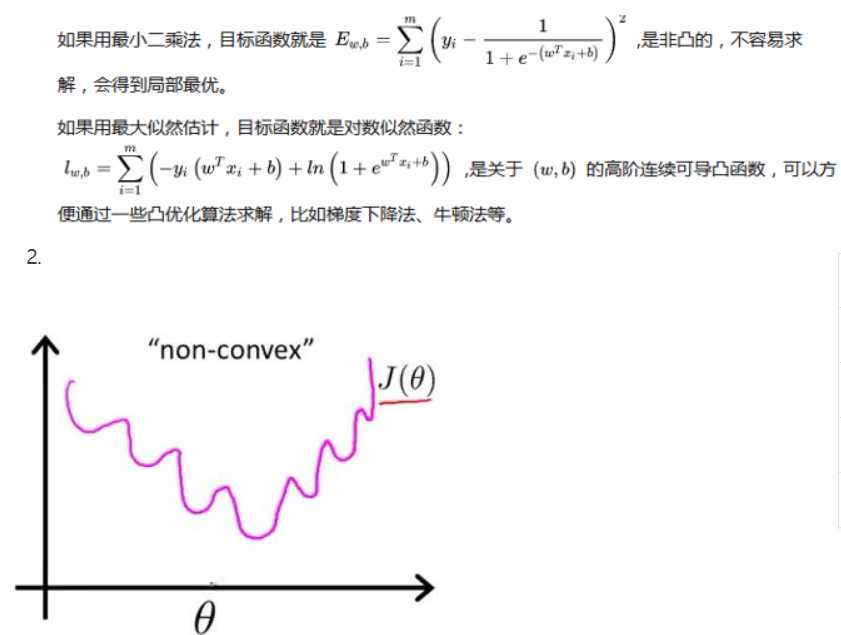
逻辑回归为什么使用对数损失函数
逻辑回归的损失函数是它的极大似然函数。损失函数一般有四种,平方损失函数,对数损失函数,HingeLoss0-1损失函数,
绝对值损失函数。将极大似然函数取对数以后等同于对数损失函数。在逻辑回归这个模型下,对数损失函数的训练求解参数的速度是比较快的。

其中对数损失在单个数据点上的定义为:
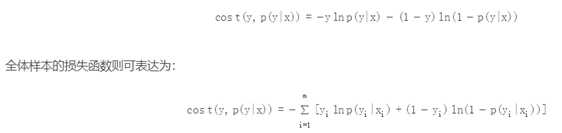
可以看到,这个对数损失函数与上面的极大似然估计的对数似然函数本质上是等价的。
为什么不选平方损失函数的呢?
其一是因为如果你使用平方损失函数,你会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。
sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。
逻辑回归算法

逻辑回归如何分类
逻辑回归作为一个回归(也就是y值是连续的),如何应用到分类上去呢。y值确实是一个连续的变量。逻辑回归的做法
是划定一个阈值,y值大于这个阈值的是一类,y值小于这个阈值的是另外一类。阈值具体如何调整根据实际情况选择。
一般会选择0.5做为阈值来划分。
逻辑回归的求解方法
由于该极大似然函数无法直接求解,我们一般通过对该函数进行梯度下降来不断逼近最优解
因为就梯度下降本身来看的话就有随机梯度下降,批梯度下降,small batch 梯度下降三种方式。
简单来说 批梯度下降会获得全局最优解,缺点是在更新每个参数的时候需要遍历所有的数据,计算量会很大,并且会有
很多的冗余计算,导致的结果是当数据量大的时候,每个参数的更新都会很慢。
随机梯度下降是以高方差频繁更新,优点是使得sgd会跳到新的和潜在更好的局部最优解,缺点是使得收敛到局部最优解
的过程更加的复杂。
小批量梯度下降结合了sgd和batch gd的优点,每次更新的时候使用n个样本。减少了参数更新的次数,可以达到更加稳定
收敛结果,一般在深度学习当中我们采用这种方法
逻辑回归优缺点:
优点:容易使用和理解

缺点:
1.不适合处理复杂数据。因为形式非常的简单
2.很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.
我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好
3.容易产生过拟合
标签:获得 深度学习 超出 最小二乘法 过程 数据 形式 图片 mic
原文地址:https://www.cnblogs.com/Lazycat1206/p/11942985.html