标签:漏洞 ssis 它的 写用 不用 ber html ace 很多
首先,该如何评审自己写的测试用例是否满足测试要求?是否存在漏洞与缺陷?
这就要引入一个测试覆盖率的概念了。
测试覆盖率
覆盖率是用来度量测试完整性的手段,是测试效果衡量的标准,是测试技术有效性的度量:
覆盖率 = (至少被执行一次的项目(item)数) / (项目的总数)
项目是指:语句、判定、分支、函数等等。
覆盖率按照测试方法一般可分为三大类:
另外还包括面向对象覆盖率等。
注意,测试用例设计不能一味的追求覆盖率,因为测试成本随覆盖率的增加而增加,要在覆盖率和成本之间有所取舍。
白盒覆盖率中使用的最常见的就是逻辑覆盖率(Logical Coverage),也称为代码覆盖率(Code Coverage)、或者称为结构化覆盖率(Structural Coverage)。
逻辑覆盖率包括:
语句覆盖(Statement Coverage)的含义是,在测试时运行被测程序后,程序中被执行到的可执行语句的比率:
语句覆盖率 = (至少被执行一次的语句数量) / (可执行的语句总数)
现在我们祭出在测试覆盖率篇中都会使用的一张图。
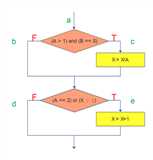
这个一个函数的流程图,需要传入三个参数;有两个语句,每个语句中有两个判断条件;根据传入参数的不同,它有几种可能的执行过程:abd、abe等等。牢记这张图。
我们用Python代码实现这个函数:
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
if a == 2 or x > 1:
x = x + 1
case1 = foo(a=2, b=0, x=3)
case2 = foo(a=2, b=1, x=3)上面的示例中,我们分别写了两个用例case1和case2。
那么它们的用例怎么设计呢?又怎么计算语句覆盖率呢?
在测试时,首先设计若干个测试用例,然后运行被测程序,使程序中的每个可执行语句至少执行一次。
首先来看case1,在函数foo中,因为每个语句都包含两个子条件,所有共有4个语句,当然,你也可以只根据大的语句来划分,那就是2个语句。
根据case1的传入参数a=2, b=0, x=3,它符合:
| 编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1 | T |
| 2 | B==0 | T |
| 3 | A==2 | T |
| 4 | X>3 | F |
在程序运行中,上面4种情况都会覆盖到,所以,根据上面的公式:
被执行的语句是4条除以可执行的语句总数4条,它的覆盖率是100%。
而case2,根据传入参数a=2, b=1, x=3:
| 编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1, B==0 | T,F |
| 2 | A==2, X>1 | T,F |
因为and的关系,上面第一条语句不会执行。所以,它的覆盖率50%。
需要注意的是,有时候语句覆盖率达到100%也会有缺陷发现不了,比如开发人员将第二个语句写成了and:
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
if a == 2 and x > 1: # 偷偷将 or 替换为 and
x = x + 1
case1 = foo(a=2, b=0, x=3)
case2 = foo(a=2, b=1, x=3)自己算覆盖率吧!
所以覆盖率只是我们度量的一个手段。
判定覆盖(Decision Coverage)也叫分支覆盖(Branch Coverage),它是指在测试时运行被测试程序后,程序中所有判定语句的取真分支和取假被执行到的比率:
判定覆盖率 = (判定结果被评价的次数) / (判定结果的总数)
一般的判定条件可能有这些:if、if\else、if\elif\else等等。
这个怎么玩呢?把最开始的程序图拿过来(你想象它在这!)。
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
if a == 2 or x > 1:
x = x + 1
case1 = foo(a=2, b=0, x=3)
case2 = foo(a=1, b=0, x=1)我们设计了两个用例,来判断取真取假的情况。
来看case1,参数是a=2, b=0, x=3:
| 编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1, B==0 | T |
| 2 | A==2, X>1 | T |
在来看case2,参数是a=1, b=0, x=1:
| 编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1, B==0 | F |
| 2 | A==2, X>1 | F |
case1走了两次真,case2走了两次假,我们认为这两个用例的判定覆盖率达到了100%:
需要注意的是,有时候语句覆盖率达到100%也会有缺陷发现不了,比如开发人员将第二个条件语句的X>1写成了X<1它的执行情况是:
| 用例 | 编号 | 条件取值 | 标记 |
|---|---|---|---|
| case1 | 1 | A>1, B==0 | T |
| case1 | 2 | A==2, X>1 | T |
| case2 | 3 | A>1, B==0 | F |
| case2 | 4 | A==2, X<1 | F |
此时的判定覆盖率仍然为100%,但是程序已经存在问题了。
条件覆盖(Condition Coverage)的含义时,在测试时运行被测程序后,所有的判断语句中每个条件的可能取值(真和假)出现过的比率:
条件覆盖率 = (条件操作数值至少被评价一次的数量) / (条件操作数的总数)
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
if a == 2 or x > 1:
x = x + 1
case1 = foo(a=2, b=0, x=3)
case2 = foo(a=1, b=0, x=1)
case3 = foo(a=2, b=1, x=1)这个又该怎么玩呢?
我们在设计用例时,要使每个判断中的每个条件的可能值都要满足一次,这么说,上面的程序有4个语句,每个语句都有两种情况,所以,共有八种情况:
| 条件 | 取真 | 取假 | 标记 |
|---|---|---|---|
| A>1 | T | F | T,F |
| B==0 | T | F | T,F |
| A==2 | T | F | T,F |
| X>1 | T | F | T,F |
设计测试用例(看着那个图!):
| 测试用例 | 参数:A B X | 执行路径 | 覆盖条件 |
|---|---|---|---|
| case1 | 203 | ace | T,T,T,T |
| case2 | 101 | abd | F,T,F,F |
| case3 | 211 | abe | T,F,T,F |
case1执行了四个真,case2执行了三个假,漏掉一个假,所以,我们又设计了case3来补上这个假,最终它们的条件覆盖率是:
八种情况都覆盖了。
没完!覆盖了条件的测试用例不一定覆盖了分支:
| 测试用例 | 参数:A B X | 执行路径 | 覆盖条件 |
|---|---|---|---|
| case1 | 103 | abe | F,T,F,T |
| case2 | 211 | abe | T,FT,F |
八种条件都走完了,但是用例少覆盖了分支acd。
判定条件覆盖率(Decision Condition Coverage)也叫分支条件覆盖率(Branch Condition Coverage)。所谓判定条件覆盖就是设计足够的测试用例,使得判断中每个条件的所有可能取值至少执行一次,同时每个判断本身的所有可能判断结果至少执行一次:
判定条件覆盖率 = (条件操作数值或判定结果至少被评价一次的数量) / (条件操作数值 + 判定结果总数)
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
if a == 2 or x > 1:
x = x + 1
case1 = foo(a=2, b=1, x=3)
case2 = foo(a=0, b=0, x=1)我们先单独算出来case1的条件覆盖率和判定覆盖率。
先来看条件的:
| 条件 | 取真 | 取假 | 标记 |
|---|---|---|---|
| A>1 | T | F | T,F |
| B==0 | T | F | T,F |
| A==2 | T | F | T,F |
| X>1 | T | F | T,F |
因为是8个条件。所以结果是4/8,覆盖率也是50%。
再来看判定,参数是a=2, b=1, x=3:
| 编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1, B==0 | T,F |
| 2 | A==2,X>1 | T,T |
虽然4个条件得的结果是TFTT,但由于第一个条件是and,而结果是TF,所以,不执行,所以结果是2/4,覆盖率是50%。
那么判定条件覆盖率怎么算呢?
在来个示例,看看case2的,参数是a=0, b=0, x=1。
先来看条件的:
| 编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1, B==0 | F,T |
| 2 | A==2,X>1 | F,F |
因为是8个条件(四个语句分别取真假)。所以结果是4/8,覆盖率也是50%。
再来看判定,参数是a=0, b=0, x=1:
| 条件 | 取真 | 取假 | 标记 |
|---|---|---|---|
| A>1,B==0 | T | F | F,T |
| A==2,X>1 | T | F | F,F |
4个语句得的结果是FTFF,所以结果是2/4,覆盖率是50%。
最后的判定条件覆盖率仍然是6/12。
再说条件覆盖率之前先来看个示例:
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
if a == 2 or x > 1:
x = x + 1
case1 = foo(a=2, b=0, x=3)
case2 = foo(a=1, b=1, x=1)上例中,两个用例的判定:
| 用例名 | 取值 | 标记 |
|---|---|---|
| case1:203 | A>1,B==0 | T,T |
| case1:203 | A==2,X>1 | T,T |
| case2:111 | A>1,B==0 | F,T |
| case2:111 | A==2,X>1 | F,F |
汇总一下,两个用例的判定都覆盖到了,所以是4/4。
而条件覆盖率:
| 用例名 | 取值 | 标记 |
|---|---|---|
| case1:203 | A>1,B==0 | T,T |
| case1:203 | A==2,X>1 | T,T |
| case2:111 | A>1,B==0 | F,F |
| case2:111 | A==2,X>1 | F,F |
8个条件都覆盖到了,所条件覆盖率是8/8,那么,它们的判定条件覆盖率是12/12:
也就是说,现在判定条件覆盖率是100%。
现在,开发把上面两个条件的and 和or条件互换了。那么用上面的两个case它们的判定条件覆盖率同样是100%。
def foo(a, b, x):
if a > 1 or b == 0:
x /= a
if a == 2 and x > 1:
x = x + 1
case1 = foo(a=2, b=0, x=3)
case2 = foo(a=1, b=1, x=1)判定:
| 用例 | 取值 | 标记 |
|---|---|---|
| case1:203 | A>1,B==0 | T,T |
| case1:203 | A==2,X>1 | T,T |
| case1:111 | A>1,B==0 | F,F |
| case2:111 | A==2,X>1 | F,F |
两个用例的判定仍然是4/4。条件是8/8,那么判定条件覆盖率是12/12,最终的结果是100%。所以开发写错了代码,这两个用例仍然没有发现这类问题。
针对这类问题,就要使用条件组合覆盖率了。
条件组合覆盖(Multiple Condition Coverage)的基本思想是设计足够的测试用例,使每个判定中条件的各种可能的组合都至少出现一次:
条件组合覆盖率 = (条件组合至少被评价一次的数量) / (条件组合总数)
同样是上面的示例。
每个判断中所有的组合都要覆盖到。
| 组合编号 | 条件取值 | 标记 |
|---|---|---|
| 1 | A>1,B==0 | T,T |
| 2 | A>1,B!=0 | T,F |
| 3 | A<=1,B==0 | F,T |
| 4 | A<=1,B!=0 | F,F |
| 5 | A==2,X>1 | T,F |
| 6 | A==2,X<=1 | T,F |
| 7 | A!=2,X>1 | F,T |
| 8 | A!=2,X<=1 | F,F |
两个判定,每个判定中有两个条件,所有共有八种条件,所以,要想达到条件组合覆盖率100%的话,这八种情况都要覆盖到。
| 测试用例 | 参数:A B X | 覆盖组合编号 | 所走路径 | 覆盖条件 |
|---|---|---|---|---|
| case1 | 203 | 1,5 | ace | TTTT |
| case2 | 211 | 2,6 | abe | TFTF |
| case3 | 103 | 3,7 | abe | FTFT |
| case4 | 111 | 4,8 | abd | FFFF |
PS:覆盖组合编号内容是上上表中的组合编号。
上例中的四个测试用例覆盖了所有的条件、分支。
所以,条件组合覆盖率是100%的话,那么,条件、判定、语句都会达到100%。
但从程序运行路径角度来看,仅覆盖了3条路径,遗漏掉了acd。
所以,目前为止,并没有一种覆盖率能保证测试覆盖率达到100%。
路径覆盖(Path Coverage)是指在测试时运行被测程序后, 程序中所有可能的路径被执行过的比率。
路径覆盖率 = (至少被执行到一次的路径数) / (总的路径数)
还是那个示例,还是那个图!
如果你看着图的话, 程序执行的路径有以下几条:
| 测试用例 | 参数:A B X | 覆盖路径 |
|---|---|---|
| case1 | 203 | ace |
| case2 | 101 | abd |
| case3 | 211 | abe |
| case4 | 301 | acd |
所以,我们设计的测试用以,要把这些路径都要覆盖到。
看着采用路径覆盖率好使,但是仍然不是完美的。
如果开发将程序写错成了:
def foo(a, b, x):
if a > 1 and b == 0:
x /= a
# if a == 2 or x > 1: # 正确的
if a == 2 and x >= 1: # 开发写错后的
x = x + 1那么,在这个错误示例中,用上面的几个用例,仍然每个路径都能覆盖到,但是这个错误却不能发掘出来。
所以说,每种覆盖率都有自己的局限性,因此在测试中, 要把各种覆盖率组合起来对测试用例进行综合考量。
一般的,我们选择覆盖率优先级是:
在白盒这里的几种覆盖率,大致就是这些,我们来看其他的。
灰盒覆盖率这主要包括:
函数覆盖(Function Coverage)是针对系统或者一个子系统测试,它表示在该测试中,有那些函数被测试到了。其被测到的频率有多大,这些函数在系统所有函数中的比例有多大,函数覆盖是一个比较容易自动化的技术:
函数覆盖 = (至少被执行一次的函数数量) / (系统中函数的总数)
假如有100个函数,在测试过程中,有90个函数(至少被执行了一次的函数)被测试到了, 所以它的覆盖率是90%。
也有很多测试工具提供了了函数覆盖,比如说TrueCoverage、PureCoverage等。
接口覆盖(Interface Coverage)也叫做入口点覆盖(Entry-Point Coverage),要求通过设计一定的用例使系统的每个接口被测试到:
接口覆盖率 = (至少被执行一次的接口数量) / (系统中接口的总数)
被测试的接口可能是对外提供访问的接口,也可能是内部接口。
接口可是是函数与函数之间,模块与模块之间,子系统与子系统之间的接口。
我们主要关注接口之间的数据交换、有没有逻辑依赖等等。
比如有两条测试用例去测试4个接口,那么覆盖到了其中的两个,那么它的接口覆盖率是2/4。
黑盒测试主要应用在系统测试阶段,那么在系统测试阶段,它的测试过程一般是这样的。
所以,在黑盒覆盖率这块,主要就是做功能覆盖率(Functional Coverage)。
而在功能覆盖率中最常见的是需求覆盖(Requirement Coverage),其含义是通过设计一定的测试用例,要求每个需求点都被测试到。
需求覆盖率 = (被验证到的需求数量) / (总的需求数量)
功能覆盖方面的自动化工具比较少。
当然,以上是针对系统测试阶段来划分的。
当然,单元测试阶段,也能进行黑盒测试。
比如,我们对一个函数进行测试。我们可以把函数当成一个黑匣子,我们关注入参和返回的两边数据即可,而不用特意关注函数内部的实现。
结构化覆盖率用来度量测试的完整性已经被大家所接受,但是这个技术在面向对象领域却遇到挑战,由于传统的结构化度量没有考虑面向对象的一些特性,如继承、封装、多态。
继承对覆盖率度量的影响
class Base(object):
def foo(self): pass
def bar(self): pass
class Derived(Base):
def foo(self): pass
case1 = Derived().foo()
case2 = Derived().bar()
# 要考虑到面向对象的继承关系
case3 = Base().foo()
case4 = Base().bar()上例中,如果我们的用例不仅要测试到派生类的两个方法,虽然它背后也调用了基类的方法,但要考虑到继承的概念,要让基类自己执行自己的方法。
基于状态的类的覆盖率特点
来举个栈的示例。
class Stack(object):
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
def pop(self):
self.items.pop()
p = Stack()
p.push(‘a‘) # case1
p.pop() # case2现在,站在灰盒测试的角度来说,通过测试出栈和入栈的操作,已经达到了测试的效果了。
这就完了么?没有!因为我们没有考虑到栈的特点,比如,我们有没有考虑,如果栈为空,你做出栈操作,会不会抛出异常?
如果这是个有边界限制的栈,栈满了,你还能做入栈操作吗?
所以,我们要考虑到栈的各种情况。
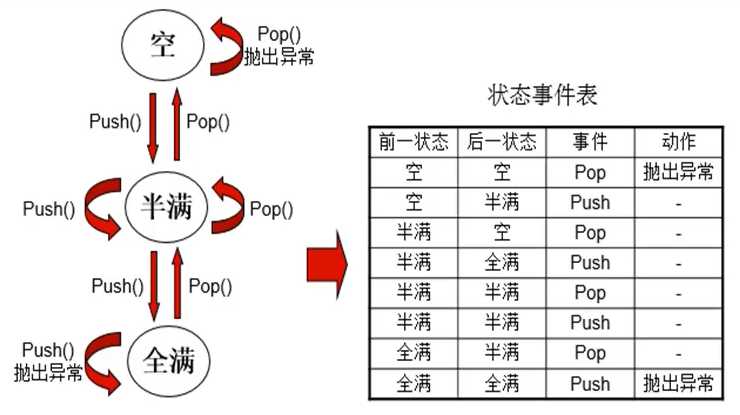
根据这些状态,来针对性写用例。
最后,从测试方法来说,有白盒、黑盒、灰盒。
当然,在平日没有必要将彼此划分的很清楚,因为我们学习覆盖率的目的是用来度量测试完整性的手段,只是验证测试效果的一种衡量标准。
还是要根据项目、测试阶段、测试方法不同,来采用不同的测试覆盖率。
标签:漏洞 ssis 它的 写用 不用 ber html ace 很多
原文地址:https://www.cnblogs.com/sundawei7/p/11944489.html