标签:最小 make 参数 公式 机器学习 增加 def 就会 大量
在Andrew Ng的机器学习课程里面,讲到使用梯度下降的时候应当进行特征缩放(Feature Scaling)。进行缩放后,多维特征将具有相近的尺度,这将帮助梯度下降算法更快地收敛。 为了解释为什么特征缩放会帮助梯度下降算法更快地收敛,Andrew给了两幅图来解释:
Feature Scaling
Idea: Make sure features are on a similar scale.
E.g.
归一化前,代价函数关于参数
??和
??的关系等高线图可能如下图:
而如果进行了,归一化,那么其等高线图可能就变成了下图:
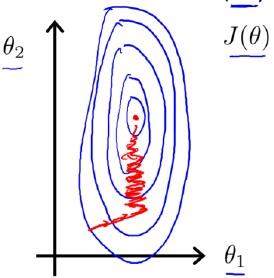
而如果进行了,归一化,那么其等高线图可能就变成了下图:
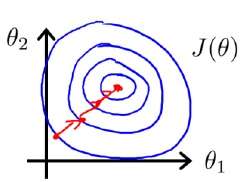
关于等高线图的变化,Andrew并没有细说原因,只是直接这么说了。一种常见的误解是:
原来和
的尺度不一样,所以等高线图是狭长的,而归一化以后,大家尺度(甚至取值范围)一样了,等高线图被压扁了,所以就是一个圆形了呗。
但是问题在于,等高线图的变量(即轴)是和
,而不是
和
!对
和
做的缩放,导致
关于
和
的等高线图产生的变化根本不是直观上的那么一目了然。
本文的目标就在于把这个问题解释清楚:对和
的缩放是怎么把以
,
为变量的
等高线图变得更加圆,从而使得梯度下降效率变高的。
首先我们把问题定义一下,我们是要预测房价,目前有两个特征:
– : 面积,以平方英尺计,取值范围在0 ~ 2,000
– : 卧室数,取值范围在0 ~ 5
假设,房价是关于这两个特征的线性关系:
那么,在进行梯度下降的时候,目标最小化的代价函数(Cost Function)则为:
在缩放(scaling)前,由于的尺度比较大(0 ~ 2,000),而
的尺度小(0 ~ 5),因此
和
同等大小的变化,对
的影响差距巨大,即
对
影响要比
大很多。进而,会造成
对
更加敏感(即
的单位变化比
的单位变化对
的影响更大)。因此在等高线图上,在
方向上更扁平,即较小的变化会造成
取值的剧烈变化,而在
方向上更加狭长,即较大的变化才会造成
取值的较大变化。
那么缩放(scaling)以后,和
的尺度是一致的,故
和
同等大小的变化,对
的影响不再含有特征尺度上的因素,这也同样反映在
上。那么在等高线图上的表现就是,在
方向上等高线图会拉长,即
对
相较于缩放前变得"迟钝"了。
如果我们只观察和
,那么二者的关系在进行特征缩放前后的图形可能如下:
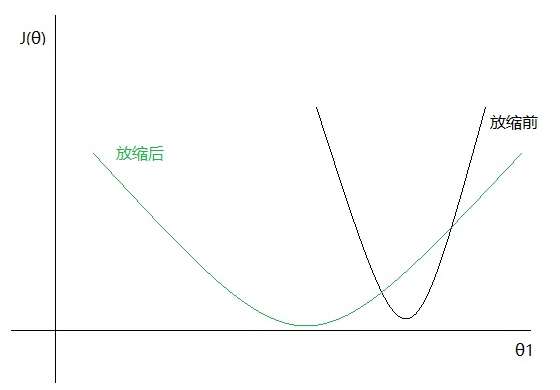
即关于
更加缓和,且在
上被拉长了(缩放后,参数
的最优解跟缩放前几乎不会是同一个值,因此上图中
的最小值点对应的
值并不相同)。
因此,Andrew的缩放前后的图形,并不是在(纵轴)方向上被压扁了,而是在
(横轴)方向上被拉长了!
而从梯度下降迭代上看,每次迭代使用的公式为:
注意到,每次迭代的时候,的更新幅度是和
相关的,因此如果某个
的尺度相较其他维度特征大很多的话,势必造成该维度对应的参数
的更新非常剧烈,而其他维度特征对应的参数更新相对缓和,这样即造成迭代过程中很多轮次实际上是为了消除特征尺度上的不一致。
另一个角度,实际上就是当前
的梯度方向,它和
是相关的,因为对于而言,
是它的参数。所以,当我们迭代更新
的时候,梯度下降的方向会因特征
的尺度产生剧烈变化,即在尺度大(导致梯度大)的方向上持续迭代。而这种变化显然不是迭代的目的,它仅仅是为了消除尺度差距上的悬殊。
故,因为的梯度是跟特征
取值相关的,而梯度下降迭代就是不断在梯度方向上寻找最优点。所以如果特征在尺度上差距显著,那么迭代中就会有一些(甚至大量)轮次主要在抹平尺度上的差异。在理论上,如果迭代轮次足够多,仍然能够得到最优解,但在实际中往往会限定一个迭代轮次上限,可能会出现找到的解并不是最优解。
因为要抹平尺度上的差异,迭代到最优解的轮次势必增加,即表现为常说的"收敛速度慢"。
标签:最小 make 参数 公式 机器学习 增加 def 就会 大量
原文地址:https://www.cnblogs.com/bind/p/11956095.html