标签：int   输入   最大的   怎么   ges   宽度   ace   使用   ++   

直方图最大矩形面积

这是一个栈的应用题，利于深入了解栈的原理和功能，每次存元素的索引，遇到小的就触发，开始依次往左出栈，算的时候算到该的最右边，就实现了。注意长度是多少和栈里面现在都是递增，最后怎么处理，了解运行机制

一个直方图是由许多矩形组成的，要求在给定的直方图中找出最大的矩形面积。假定直方图矩形数量不超出1000个。

假定所有矩形的宽度都为1个单位 。如下图所示的直方图中有7个矩形，高度分别是6，2，5，4，5，1，6，其中连续的矩形能组成的最大的矩形面积是12。

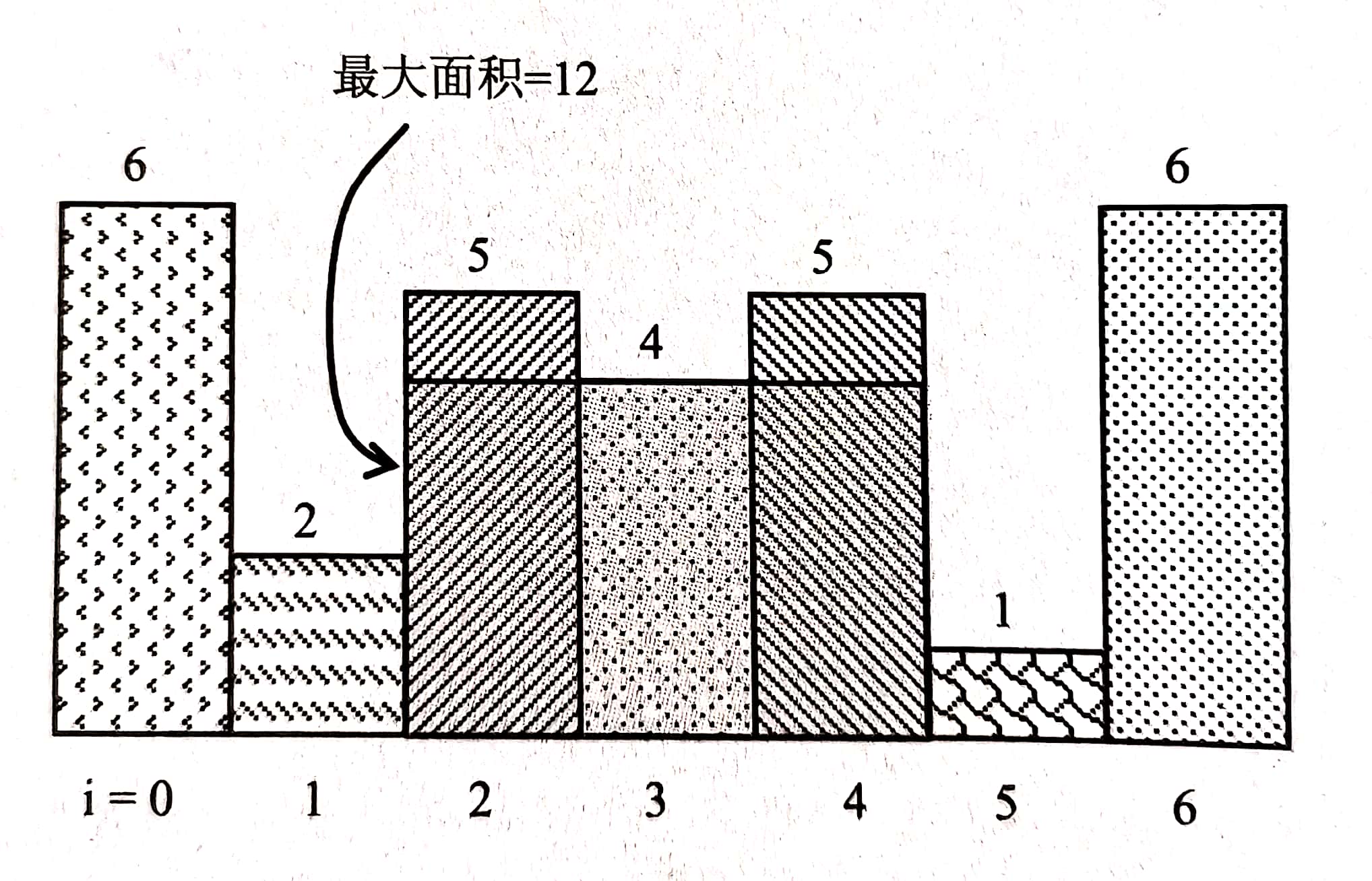
实现提示：考虑使用栈解决此问题。

输入格式:

第一行输入直方图中矩形的数量。 第二行输入一组直方图的高度，每个高度用空格符间隔。

输出格式:

输出连续矩形能组成的最大矩形面积。

输入样例:

在这里给出一组输入。例如：

7
6 2 5 4 5 1 6

输出样例:

在这里给出相应的输出。例如：

12

AC代码

#include<iostream>
#include<cstdio>
#include<stack>
#include<cmath>
using namespace std;
int main()
{
    int maxs=0,i,h[1010],n,t;
    stack <int> s;
    cin>>n;
    for (i=0;i<=n-1;i++)
      scanf("%d",&h[i]);
    i=0;
    while (i<=n-1)
    {
        if (s.empty() or h[s.top()]<=h[i])
          s.push(i++);
        else
        {
            t=s.top();
            s.pop();
            maxs=max(maxs,h[t]*(s.empty() ? i : (i-s.top()-1)));//触发的i和次峰值之间的（峰值左面都是比他高的，不在栈里，已经出栈、处理过，栈里面存的是地址）长度，空就说明都是比他大的
        }
    }
    while (!s.empty())
    {
        t=s.top();
        s.pop();
        maxs=max(maxs,h[t]*(s.empty() ? i : (i-s.top()-1)));
    }   
    cout<<maxs;
    return 0;
}

栈的灵活实际应用——直方图最大矩形面积

标签：int   输入   最大的   怎么   ges   宽度   ace   使用   ++   

原文地址：https://www.cnblogs.com/IamIron-Man/p/11956822.html