标签：flag   fail   sea   class   title   cpp   als   时间复杂度   问题：   

kmp

问题：有两个字符串，S为主串（长度为n），T为模式串（长度为m），其中n>m，如何判断T是否为S的子串

样例：
abbaabbaaba
abbaaba

朴素解法：
S从头开始遍历，以每个字母为开头，再遍历T看是否匹配。

如何降低时间复杂度？
第一次匹配时，到了第七个字符发现不匹配，那么我们S不回退，只在T上进行回退，利用S前面已知信息，快速定位，进行匹配。

如何利用已知信息？
next数组，next[i]表示模式串T前i个字符的最长相同前缀后缀的长度。
abbaab 的前缀有 a,ab,abb,abba,abbaa
abbaab 的后缀有 b,ab,aab,baab,bbaab
所以next[i]=2
可以得到S第五个第六个字符和T前两个字符相同，我们不需要再次进行比较，直接比较下一个（next[i]+1）即可

next数组的求取？
自己和自己进行匹配

next[1]=0;
    //先处理出next数组，无非是b和自己匹配，与b和a匹配一样，故代码差不多
    for(int i=2;i<=lb;i++){
        while(j>0 && b[i]!=b[j+1]) j=next[j];//往前翻记录了有相同前缀的j
        if(b[i]==b[j+1]) j++;//i匹配成功了，i继续往后
        next[i]=j;
    }
    j=0;
    for(int i=1;i<=la;i++){
        while(j>0 && a[i]!=b[j+1]) j=next[j];
        if(a[i]==b[j+1]) j++;
        if(j==lb){
            flag=1;
            printf("%d\n",i-lb+1);
            break;
        }
    }

Trie（字典树）

用于实现字符串快速检索的多叉树

问题：给出n个单词构成一个字典，再给一个单词，问此单词在字典中有没有出现。

解法：
用n个单词建成一棵树，在树上查找指定单词。

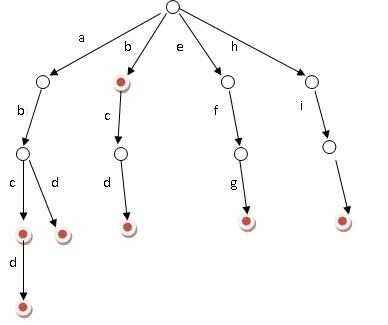
插入单词（构建Trie树）
1、初始化
Trie树为空，只包含根结点
2、插入
对于Trie树，我们从根结点开始，设该节点为P；对于这个单词，我们从第一个字母开始，设此字符为s
（1）扫描P下方的所有边，看s有没有出现过
如果出现了，设s与P→Q这条边上的字符相同，则P=Q
如果没有出现，另建一条边，使该边上的字母为s，新节点为Q，然后P=Q
（2）s变为该单词的下一个字符，重复步骤2，直到扫描完整个单词为止

void insert(char *str)
{
    int len=strlen(str);
    int p=1;//1为根节点 
    for(int k=0;k<len;k++)
    {
        int ch=str[i]-'a';//'a'有时需换成'A'或'0' 
        if(!trie[p][c])//没有共同前缀，建立一个新的 
            ch[u][c]=++tot;//tot为总点数 
        p=ch[u][c];//继续向下插入单词 
    }
    end[p]=true;//标记是一个出现过的单词（图中涂红色） 
}

检索：
（1）对于Trie树，我们从根结点开始，设该节点为P；对于这个单词，我们从第一个字母开始，设此字符为s
（2）扫描P下方的所有边，看s有没有出现过
如果出现了，设s与P→Q这条边上的字符相同，则P=Q
如果没有出现，则该单词没有出现过，直接返回false
（3）s变为该单词的下一个字符，重复步骤2，直到扫描完整个单词为止
（4）扫描完成后，判断节点P有没有被标记（是不是某个出现过的单词的结尾）。如果标记了，那么该单词出现过，返回true；如果没有标记，那么该单词是词典中这个单词的前缀，返回false。

void search(char *str)
{
    int len=strlen(str);
    int p=1;
    for(int k=0;k<len;k++)
    {
        p=trie[p][str[k]-'a'];
        if(!p) return 0;
    }
    return end[p];
}

ac自动机

问题：给定n个模式串和1个文本串，求有多少个模式串在文本串里出现过

解法：
类似Trie树上跑kmp。

fail指针：
失配后跳去哪里

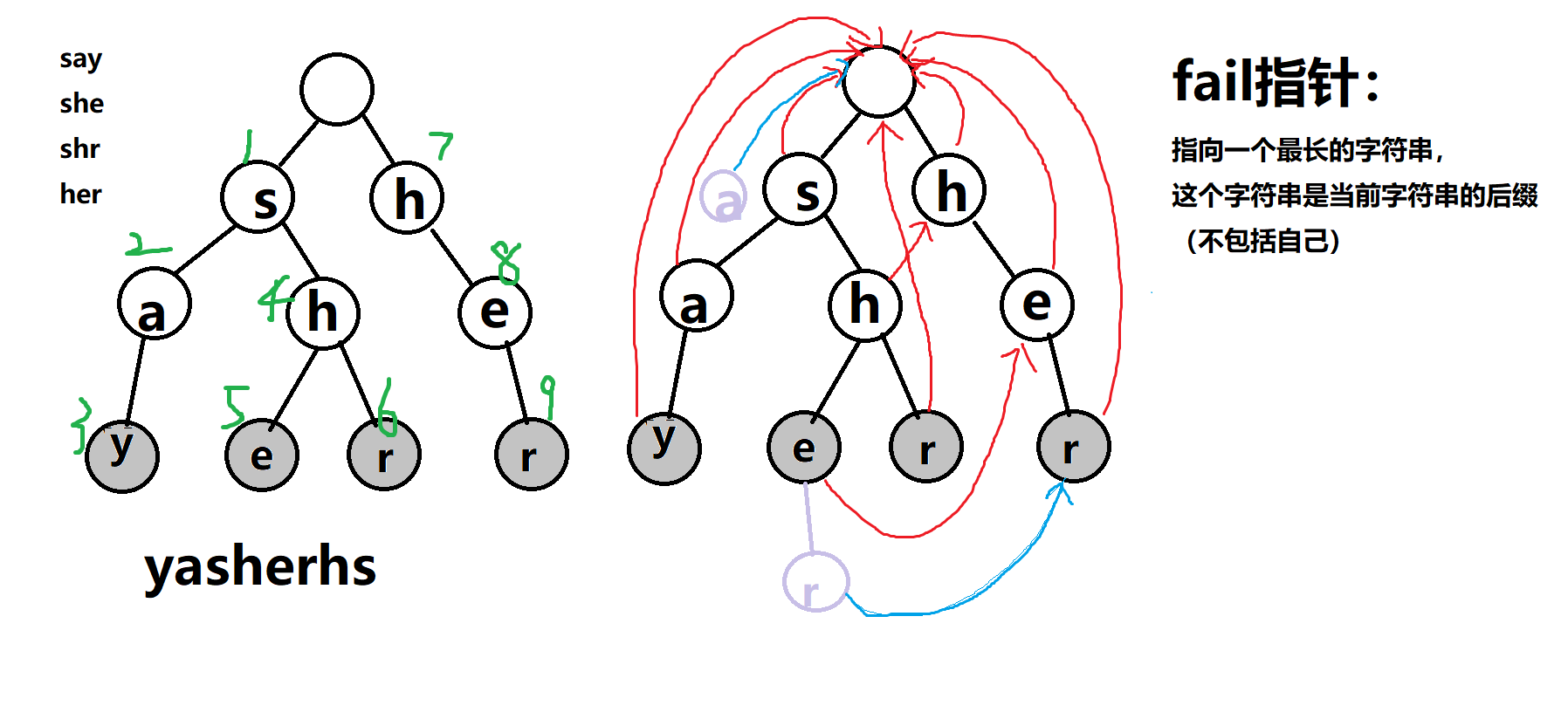
fail指针构建
通过bfs，逐层构建
1、每个模式串的首字母指向根节点
2、其余每层字母 fail指向 其父亲节点的fail指针的 和自己一样的 儿子节点

字符串

标签：flag   fail   sea   class   title   cpp   als   时间复杂度   问题：   

原文地址：https://www.cnblogs.com/qjy73/p/11967355.html