标签:二次 mamicode 绘制 math png rac image splay 相等
若关于\(x\)的方程\(\dfrac{x}{\mathrm{e}^x}+\dfrac{\mathrm{e}^x}{x+\mathrm{e}^x}+m=0\)有三个不相等的实数解\(x_1,x_2,x_3\),且\(x_1<0<x_2<x_3\),其中\(m\in\mathbb{R}\),\(\mathrm{e}\)为自然对数的底数,则\(\left( \dfrac{x_1}{\mathrm{e}^{x_1}}+1\right)^2\left(\dfrac{x_2}{\mathrm{e}^{x_2}}+1\right)\left(\dfrac{x_3}{\mathrm{e}^{x_3}}+1\right)\)的值为\((\qquad)\)
\(\mathrm{A}.1+m\) \(\qquad\mathrm{B}.\mathrm{e}\) \(\qquad\mathrm{C}.m-1\) \(\qquad\mathrm{D}.1\)
解析:
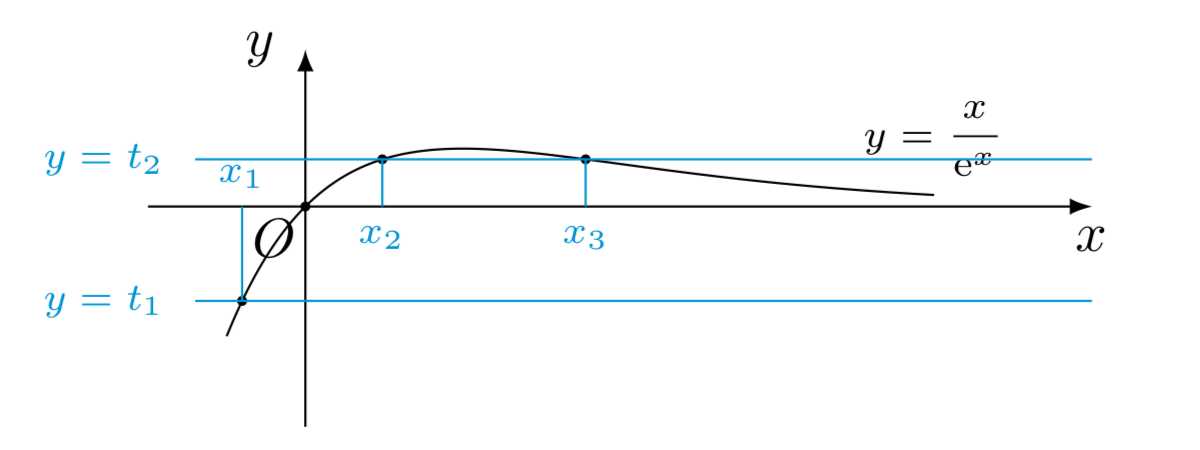
若记\[t(x)=\dfrac{x}{\mathrm{e}^x},t\neq -1.\]则\(t\)的取值范围为\(\left(-\infty,-1\right)\cup\left(-1,\dfrac{1}{\mathrm{e}}\right]\),由题可得关于\(t\)的一元二次方程\[
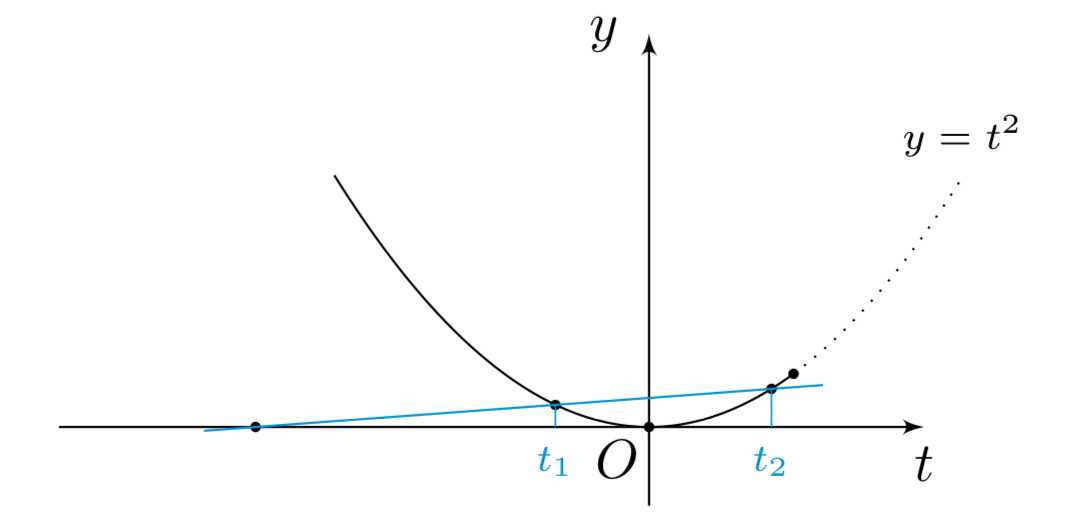
t^2=-(1+m)(t+1),t\in\left(-\infty,-1\right)\cup\left(-1,\dfrac{1}{\mathrm{e}}\right].\]如下图绘制出二次函数\(y=t^2\)与\(y=-(1+m)(t+1)\)的图象,由于关于\(x\)的方程有三个实数解,
标签:二次 mamicode 绘制 math png rac image splay 相等
原文地址:https://www.cnblogs.com/Math521/p/11991907.html