每日一题_191208

时间：2019-12-05 22:06:12 阅读：490 评论：0 收藏：0 [点我收藏+]

标签：坐标 end 图片公式椭圆 image mamicode enter img

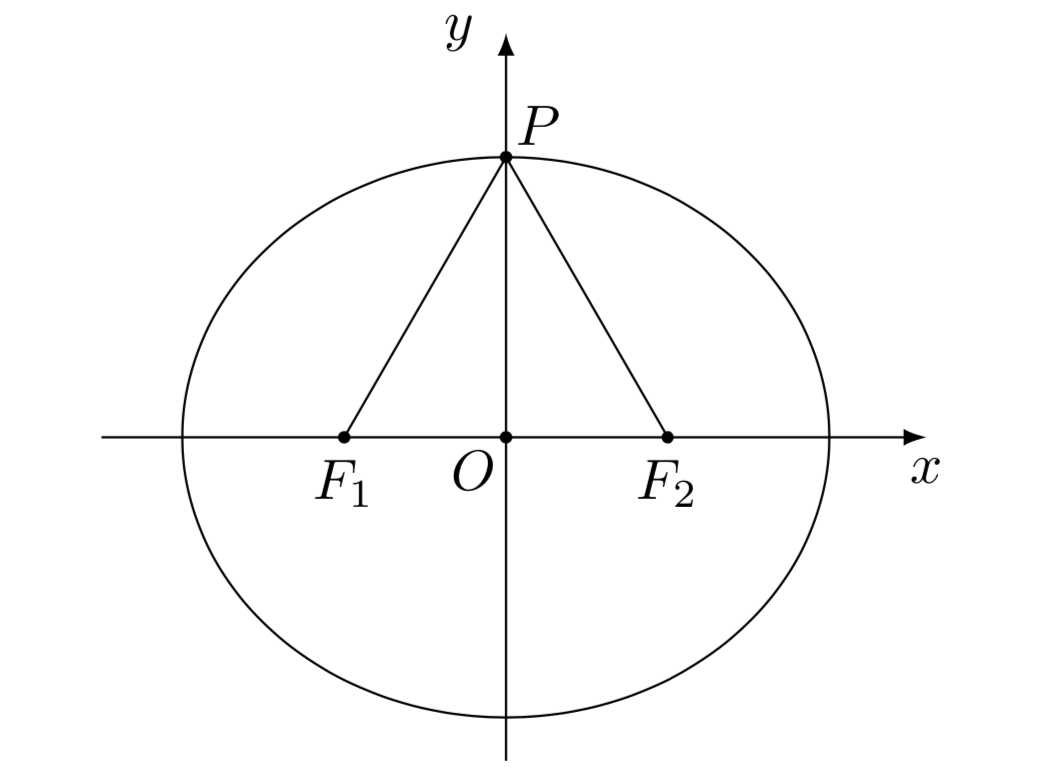
设$F_1,F_2$是椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$的左右焦点,点$P$在椭圆上, 且$\angle F_1PF_2=\dfrac{\pi}{3}$, $\triangle F_1PF_2$的外接圆的半径与其内切圆半径之比为$2:1$.
$(1)$ 求椭圆的离心率$e$;
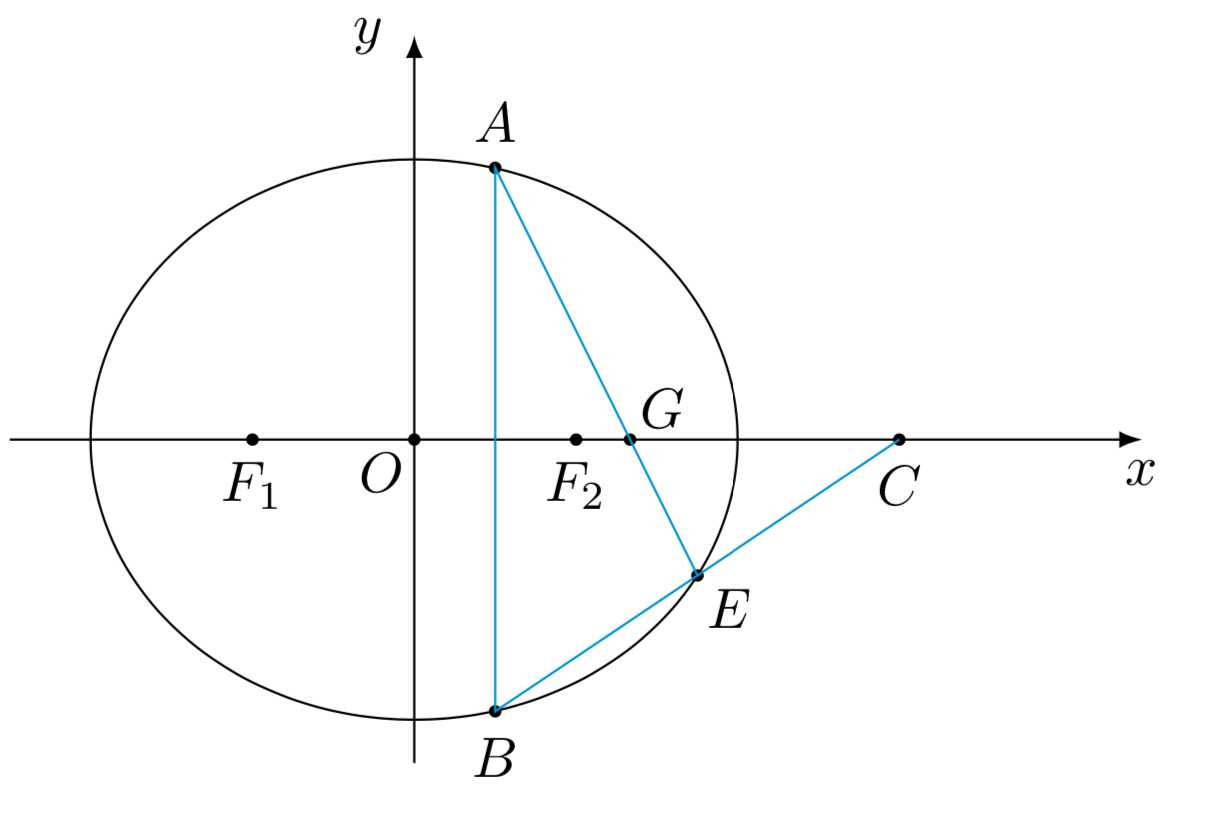
$(2)$ 设$AB$是椭圆垂直于$x$轴的弦,$C$的坐标为$(3,0)$,直线$BC$与椭圆交于点$E$,若直线$AE$恒过定点$\left(\dfrac{4}{3},0\right)$,求椭圆的方程.

技术图片

解析:
$(1)$ 设$\triangle F_1PF_2$的外接圆和内切圆半径分别为$R,r$,设$c$为椭圆的半焦距,则由正弦定理可知\[ R=\dfrac{1}{2}\cdot \dfrac{|F_1F_2|}{\sin \angle F_1PF_2}=\dfrac{2\sqrt{3}c}{3}.\]
由椭圆焦点三角形面积公式可知,$\triangle F_1PF_2$的面积\[ S_{\triangle F_1PF_2}=b^2\tan\dfrac{\angle F_1PF_2}{2}=\dfrac{\sqrt{3}}{3}b^2=\dfrac{\sqrt{3}}{3}(a^2-c^2).\]
易知$\triangle F_1PF_2$的周长为\[ L_{\triangle F_1PF_2}=|PF_1|+|PF_2|+|F_1F_2|=2(a+c).\]
由等面积法计算得$\triangle F_1PF_2$的内切圆半径长为\[ r=\dfrac{2S_{\triangle F_1PF_2}}{L_{\triangle F_1PF_2}}=\dfrac{\sqrt{3}}{3}\left(a-c\right).\]又由$R:r=2:1$可得\[ e=\dfrac{c}{a}=\dfrac 12.\]
$(2)$ 法一如图,连接$AC$,由于$A,B$关于$x$轴对称,因此直线$BC$和$AC$也关于直线$x$轴对

技术图片

称,从而$AC$与椭圆的另一个交点$M$也与$E$关于$x$轴对称,所以$M,G,B$三点共线.其中$G$的坐标为\[G\left(\dfrac{4}{3},0\right),\]
结合$(1)$可设椭圆方程为$\dfrac{x^2}{4t}+\dfrac{y^2}{3t}=1$,其中$t>0$.则$C$点位于$G$点关于椭圆的极线\[x=3t\]上.而$C(3,0)$,所以$t=1$,于是可得所求椭圆方程为$\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.
法二

技术图片

设待求椭圆方程为$\dfrac{x^2}{4t^2}+\dfrac{y^2}{3t^2}=1$,其中$t>0$,则$A,B,E$三点坐标可记为
\[ \begin{split} &A\left(2t\cos\alpha,-\sqrt{3}t\sin\alpha\right) ,\ &B\left(2t\cos\alpha,\sqrt{3}t\sin\alpha\right),\ &E\left(2t\cos\beta,\sqrt{3}t\sin\beta\right). \end{split} \]
由于$BE$直线的$x$截距为$3$,因此由截距坐标公式可得
\[ \begin{split} 3&=\dfrac{2t\cos\alpha\cdot \sqrt{3}t\sin\beta-2t\cos\beta\cdot\sqrt{3}t\sin\alpha}{\sqrt{3}t\sin\beta-\sqrt{3}t\sin\alpha}\ &=\dfrac{2t\sin\left(\beta-\alpha\right)}{\sin\beta-\sin\alpha}\ &=\dfrac{2t\cos\dfrac{\beta-\alpha}{2}}{\cos\dfrac{\beta+\alpha}{2}}. \end{split} \]
同理,由直线$AE$的$x$截距为$\dfrac{4}{3}$,可得\[ \dfrac{4}{3}=\dfrac{2t\cos\dfrac{\beta+\alpha}{2}}{\cos\dfrac{\beta-\alpha}{2}}.\]将以上两式相乘可得$
4=4t^2$,从而解得 $t=1$ ,于是所求椭圆方程为 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$.

每日一题_191208

标签：坐标 end 图片公式椭圆 image mamicode enter img

原文地址：https://www.cnblogs.com/Math521/p/11991852.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行