标签:ast splay load ilo nta math thinking 路径 形式
在transformer model出现之前,主流的sequence transduction model是基于循环或者卷积神经网络,表现最好的模型也是用attention mechanism连接基于循环神经网络的encoder和decoder.
Transformer model是一种摒弃了循环及卷积结构,仅仅依赖于注意力机制的简洁的神经网络模型。我们知道recurrent network是一种sequential model,不能很好地解决长距离依赖的问题(序列过长时,信息在序列模型中传递时容易一点点丢失),并且阻碍了parallelism within train example.而transform最引人瞩目的一点正是很好地解决了长距离依赖的问题,通过引入自注意力机制(self-attention)使得对依赖的建模与输入输出序列的距离无关,并且支持train exmaple内部的并行化。注意力机制可以参考之前写的notes of cs224n lecture8.
下图1是transformer的模型架构图
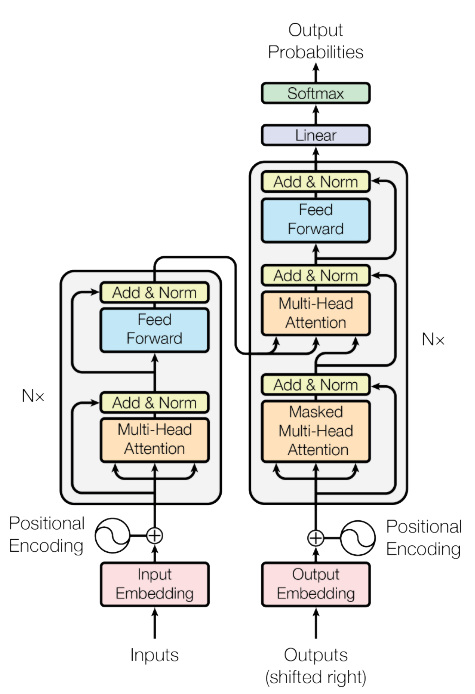
左边是encoder,右边是decoder,各有6层,下面我将讲解个人觉得比较重要的几个点。
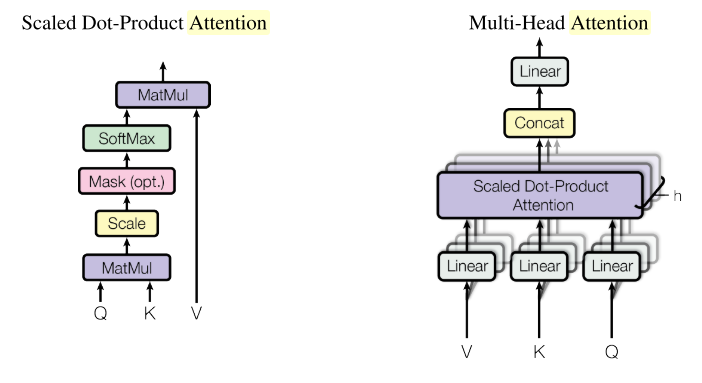
如上图2左边所示即为dot-producted attention的一般形式,在transformer中,初始Q, K, V即为一个句子所有的subword编码构成的矩阵(seq_len, d_model),其中d_model是subword的编码长度。Deocder的第二个Multi-Head Attention中的Q, K, V会有所不同,在讲解Multi-Head Attention是提到。下面是dot-producted attention的数学表达形式
\[
Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_{k}}})V
\]
这里除以\(\sqrt{d_k}\)是因为在与additive attention(之前写的文章有提到)对比时发现\(d_k\)较小时,这两种注意力机制表现相似,但是当\(d_k\)较大时dot-producted attention不如additive attention。最后分析原因发现\(d_k\)较大时\(QK^T\)点乘结果矩阵元素在数量级很大,使得softmax函数求导的梯度非常小。下面是原论文的一个解释
To illustrate why the dot products get large, assume that the components of q and k are independent random variables with mean 0 and variance 1. Then their dot product, \(q \cdot d=\sum_{i=1}^{d_k}{q_{i}k_{i}}\), has mean 0 and variance dk.
如上图2右边所示即为Multi-Head Attention的结构图。它的中心思想就是将原来的\((Q, K, V)\)转换成num_heads个shape为(seq_len, d_model/num_heads)的\((Q_i, K_i, V_i)\),然后再为每个head执行dot-producted attention的操作,最后再将所有head的输出在最后一个维度上进行拼接得到与对原始输入\((Q, K, V)\)执行单个dot-producted attention操作后shape一致的结果。下面是Multi-Attention的数学表达形式
\[
\begin{aligned} \text { MultiHead }(Q, K, V) &=\text { Concat }\left(\text { head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}} &=\text { Attention }\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned}
\]
其中,\(W^{Q}_{i} \in \mathbb{R}^{d_{model} \times d_k}, W^{K}_{i} \in \mathbb{R}^{d_{model} \times d_k}, W^{V}_{i} \in \mathbb{R}^{d_{model} \times d_k}\),而\(W^{O}_{i} \in \mathbb{R}^{hd_{v} \times d_{model}}\)
在transformer中使用h=8个parallel attention heads.对于每个head使用\(d_k=d_v=d_{model}/h=64\). 我看tf official tutorial of transformer实现中并没有为每个head学习转换矩阵\(W^{Q}_{i},W^{K}_{i},W^{V}_{i}\),而是直接对\(d_{model}\)的编码表示进行划分成h份,然后输入到各自的head中进行处理。Multi-Head Attention机制允许模型在不同位置共同关注来自不同表示子空间的信息。
Decoder中包含两层的Multi-Head Attention(MHA),第二层的MHA不再使用初始的\((Q, K, V)\)作为输入,而是使用上一层MHA的输出作为\(Q\),Encoder最后一层(第6层)的输出作为\(K, V\).
无论encoder还是decoder都需要使用mask屏蔽掉不必要的信息干扰。
对于encoder,由于我们传入的数据是padded batch,因此需要对padded的信息进行mask,具体mask的位置放置在dot-producted attention的scale即\(\frac{Qk^T}{\sqrt{d_k}}\)之后softmax之前,对需要mask的位置赋值为1e-9,这样在softmax之后需要mask的位置就变成了0,就像是指定mask的位置进行dropout.
对于decoder,每一层包含两个Multi-Head Attention(MHA),第一个MHA同样需要对padded信息进行mask,除此之外还要对output中还未出现的词进行mask,保证只能根据前面出现的词信息来预测后面还未出现的词。将两个mask矩阵叠加之后输入到dot-producted attention单元中的scale之后用于屏蔽非必要信息。第二个MHA由于使用Encoder最后一层的输出作为\(K, V\),所以需要对Encoder初始输入的padded信息进行mask,同样是在dot-producted attention单元中的scale之后操作。
encoder和decoder的输入是两套独立的embedding(例如translation task,分别是原语和目标语subword的Embeddings),embedding的维度为\(d_{model}\),论文中的base model设为512,big model设为1024.在embedding输入模型前逐元素乘以\(\sqrt{d_{model}}\),因为在dot-producted attention中 \(\frac{QK^T}{\sqrt{d_{model}}}\).
由于transform model不包含循环和卷积网络,为了使模型能利用sequence的顺序信息,必须加入序列中每个subword的相对或者绝对位置信息。因此引入了Positional Encoding,它保持和embedding一样维度\(d_{model}\),具体encoding的方式有很多种,主要分为学习的和固定的(learned and fixed)。在论文中使用了固定的无须学习的positional embedding,使用不同频率的cos和sin函数如下
\[
\begin{align}
PE_{(pos,2i)}&=sin(pos/10000^{2i/d_{model}})\PE_{(pos,2i+1)}&=cos(pos/10000^{2i/d_{model}})
\end{align}
\]
其中,pos是token position in sequence,i是dimension position.之所以选择cos和sin函数是因为对于固定的偏置量\(k,PE_{pos+k}\)能够表示为\(PE_{pos}\)的线性函数,假设它可以很容易学习到相对位置引入的信息。使用cos和sin的另一个原因是它允许模型推断比训练过程中遇到的更长的序列。论文中作者表示也使用了learned positional embeddings,但是与上述的fixed positional embeddings结果基本一致,所以最终采用了fixed positional embedings,这种方式更高效,减少训练开销。
最终作为模型输入的是token embeddings + positional embeddings,然后套一层dropout.

如上图所示,使用self-attention机制主要有三点原因
由于self-attention的complexity per layer为\(O(n^2 \cdot d)\),考虑非常长序列的极限情况,可以限制self-attention在计算时只考虑输入序列K,V中的r个邻居即可将complexity per layer限制在\(O(r \cdot n \cdot d)\),这就是上图2中的Self-Attention(restricted).
WMT 2014 English-German datasset和WMT 2014 English-French dataset,数据集官网download,论文使用其中的newstest2013作为验证集(development dataset),newstest2014作为测试集(test dataset)。base model平均最后5个checkpoint的结果,big model平均最后20个checkpoint的结果。由于数据集太过庞大,训练代价很大。论文中使用8 NVIDIA P100 GPUs,base model训练100000 steps耗时12h,big model训练300000 steps耗时3.5 days.
论文中主要使用了两种正则化手段来避免过拟合并加速训练过程。
在每一residual Multi-Head Attention之后,Add&Norm之前进行dropout,以及add(token embedding,positional encoding)之后进行dropout,FFN中没有dropout,base model的dropout rate统一设置为0.1,big model在wmt14 en-fr数据集上设置为0.1,在en-de数据集上设置为0.3
Label Smothing Regularization(LSR)是2015年发表在CoRR的paper:Rethinking the inception architecture for computer vision中的一个idea,这个idea简单又实用。假设数据样本x的针对label条件概率的真实分布为
\[
q(k|x)=\delta_{k,y}=\left\{
\begin{aligned}
1, k = y\0, k \neq y
\end{aligned}
\right.
\]
这使得模型对自己给出的预测太过自信,容易导致过拟合并且自适应能力差(easy cause overfit and hard to adapt)。解决方案:给label分布加入平滑分布\(u(k)\),一般取均匀分布\(u(k)=\frac{1}{k}\)就好,于是得到
\[
q'(k|x)=(1-\epsilon)\delta_{k,y}+\epsilon u(k)
\]
映射到损失函数cross entropy有
\[
\begin{aligned}
H(q',p)&=-\sum_{k=1}^{K}\log^{p(k)}q'(k)\&=(1-\epsilon)H(q,p)+\epsilon H(u,p)
\end{aligned}
\]
由上式可知,LSR使得不仅要最小化原来的交叉熵H(q,p),还要考虑预测分布\(p\)与\(u(k)\)之间差异最小化,使得模型预测泛化能力更好。transformer的论文中指定\(\epsilon_{ls}=0.1\)。下表是使用LSR和未使用LSR在tensorflow datasets的ted_hrlr_translate/pt_to_en dataset上bleu score对比
| bleu on validation dataset | bleu on test dataset | |
|---|---|---|
| beam_search | 0.415/41.5 | 0.420/42.0 |
| beam_search + label_smooth_regualrization | 0.473/47.3 | 0.468/46.8 |
可以看到使用了LSR在验证集和测试集上都取得了比更好的bleu score.但是LSR对perplexity不利,因为模型的学习目标变得更不确切了。
在multi-head attention之后使用layer normlization可以加速参数训练使得模型收敛,并且可以避免梯度消失和梯度爆炸。相比BatchNormalization,LayerNormalization更适用于序列化模型比如RNN等,而BatchNormalization则适用于CNN处理图像。
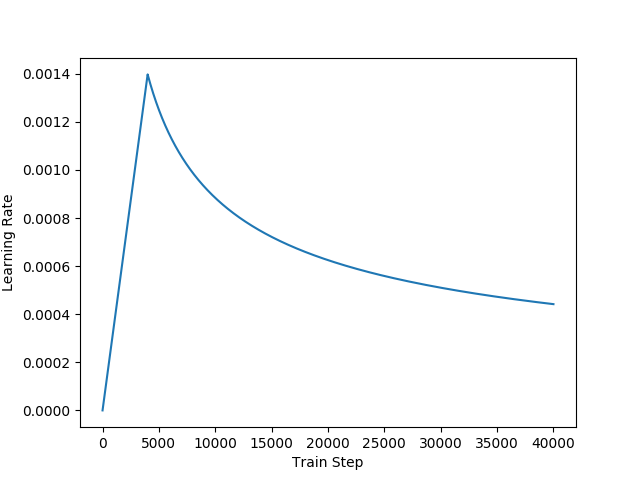
Transformer使用Adam optimizer with \(\beta_{1}=0.9,\beta_{2}=0.98,\epsilon=10^{-9}\).学习率在训练过程中会变动,先有一个预热,学习率呈线性增长,然后呈幂函数递减如上图所示,下面是学习率的计算公式
\[
lrate=d^{-0.5}_{model} \cdot min(step\_num^{-0.5},step\_num \cdot warmup\_steps^{-1.5})
\]
论文中设置warmup_steps=4000.也就是说训练的前4000步线性增长,4000步后面呈幂函数递减。这么做可以加速模型训练收敛,先以上升的较大的学习率让模型快速落入一个局部收敛较优的状态,然后以较小的学习率微调参数慢慢逼近更优的状态以避免震荡。
Transformer是NLP在深度学习发展历程上的一座里程碑,目前主流的预训练语言模型都是基于transformer的,逐渐取代了LSTM的位置,深入理解transformer的细节对后续NLP的学习非常重要。
Transformer最大的亮点在于不依靠RNN和CNN,通过引入self-attention机制,很好地解决了让人头疼的长距离依赖问题,使得输入和输出直接关联,没有了RNN那样的序列传递信息损失,输入输出之间经过的的路径长为常数级,与输入序列长度无关,上下文信息保留更完整。因此tranformer是非常强大的文本生成模型,应用于MT, 成分句法分析(constituency parsing)等效果非常好。
标签:ast splay load ilo nta math thinking 路径 形式
原文地址:https://www.cnblogs.com/brooksj/p/12001361.html