标签:自己 导致 pre 它的 二分法查找 font 绝对值 结构 二叉堆
树
一、树的定义
1,树Tree是n(n >= 0) 个结点的有限集, n = 0时 称为空树 。
在任意一棵非空的树中:
(1)有且仅有一个特定的根结点
(2)当n>1时,其余节点可分为m(m > 0)个互不相交的有限集T1,T2,.....,Tm,其中每一个集合又是一棵树,并且称为根的子树。
如下图所示
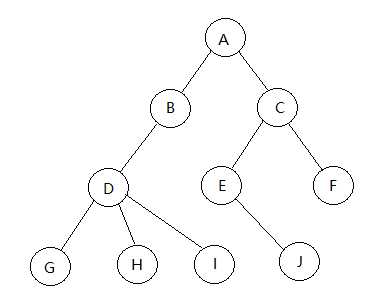
2,结点
(1)结点包含一个数据元素以及若干指向其子树的分支。
(2)结点拥有的子树数量称为结点的度
(3)度为0的结点称为叶节点或终端节点
(4)度不为0的结点称为非终端结点或分支结点
(5)一棵树的度是树内各结点的度的最大值
3,结点间的关系
结点的子树的根称为该结点的孩子,该结点称为孩子的双亲。同一个双亲的孩子之间互称兄弟。
结点的祖先是从根到该结点所经分支上的所有结点。反之,以某结点为根的子树中的任一结点都成为该结点的子孙。
二叉树
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树有如下特性:
1、每个结点都包含一个元素以及n个子树,这里0≤n≤2。
2、左子树和右子树是有顺序的,次序不能任意颠倒。左子树的值要小于父结点,右子树的值要大于父结点。
假设我们现在有这样一组数[35 27 48 12 29 38 55],顺序的插入到一个数的结构中,
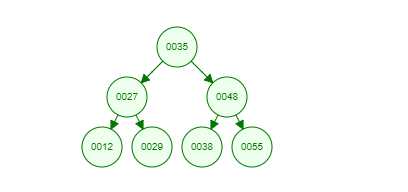
这就是一棵二叉树啦!我们能看到,经通过一系列的插入操作之后,原本无序的一组数已经变成一个有序的结构了,并且这个树满足了上面提到的两个二叉树的特性!
但是如果同样是上面那一组数,我们自己升序排列后再插入,也就是说按照[12 27 29 35 38 48 55]的顺序插入,会怎么样呢?
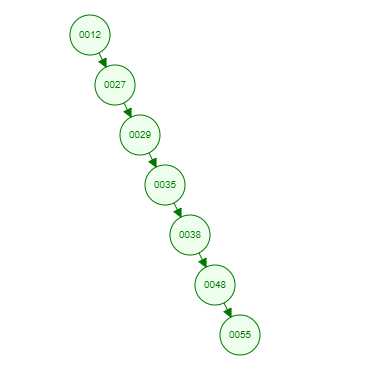
由于是升序插入,新插入的数据总是比已存在的结点数据都要大,所以每次都会往结点的右边插入,最终导致这棵树严重偏科!!!上图就是最坏的情况,也就是一棵树退化为一个线性链表了,这样查找效率自然就低了,完全没有发挥树的优势了呢!
为了较大发挥二叉树的查找效率,让二叉树不再偏科,保持各科平衡,所以有了平衡二叉树!
平衡二叉树
平衡二叉树是一种特殊的二叉树,所以他也满足前面说到的二叉树的两个特性,同时还有一个特性:
它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
大家也看到了前面[35 27 48 12 29 38 55]插入完成后的图,其实就已经是一颗平衡二叉树啦。
那如果按照[12 27 29 35 38 48 55]的顺序插入一颗平衡二叉树,会怎么样呢?我们看看插入以及平衡的过程:
![]()

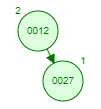
![]()
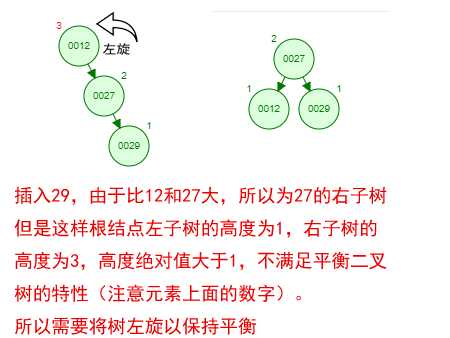
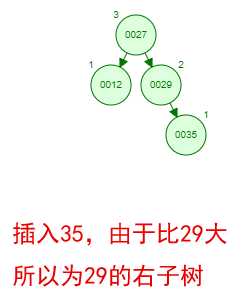
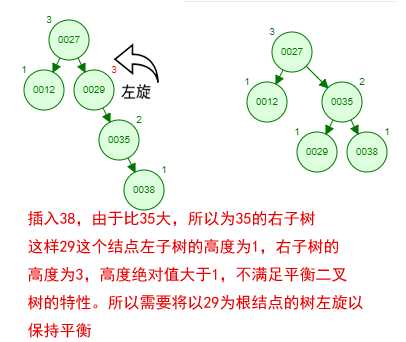
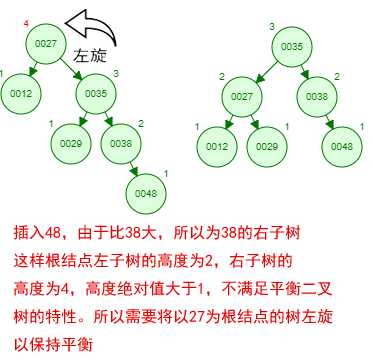
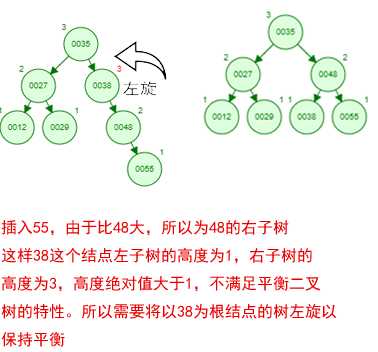
这棵树始终满足平衡二叉树的几个特性而保持平衡!这样我们的树也不会退化为线性链表了!我们需要查找一个数的时候就能沿着树根一直往下找,这样的查找效率和二分法查找是一样的呢!
一颗平衡二叉树能容纳多少的结点呢?这跟树的高度是有关系的,假设树的高度为h,那每一层最多容纳的结点数量为2^(n-1),整棵树最多容纳节点数为2^0+2^1+2^2+...+2^(h-1)。这样计算,100w数据树的高度大概在20左右,那也就是说从有着100w条数据的平衡二叉树中找一个数据,最坏的情况下需要20次查找。如果是内存操作,效率也是很高的!但是我们数据库中的数据基本都是放在磁盘中的,每读取一个二叉树的结点就是一次磁盘IO,这样我们找一条数据如果要经过20次磁盘的IO?那性能就成了一个很大的问题了!那我们是不是可以把这棵树压缩一下,让每一层能够容纳更多的节点呢?虽然我矮,但是我胖啊...
标签:自己 导致 pre 它的 二分法查找 font 绝对值 结构 二叉堆
原文地址:https://www.cnblogs.com/ljl150/p/11995907.html