正则化

标签：lin   取值   matrix   sha   strong   term   span   矩阵   sdn   

过拟合问题

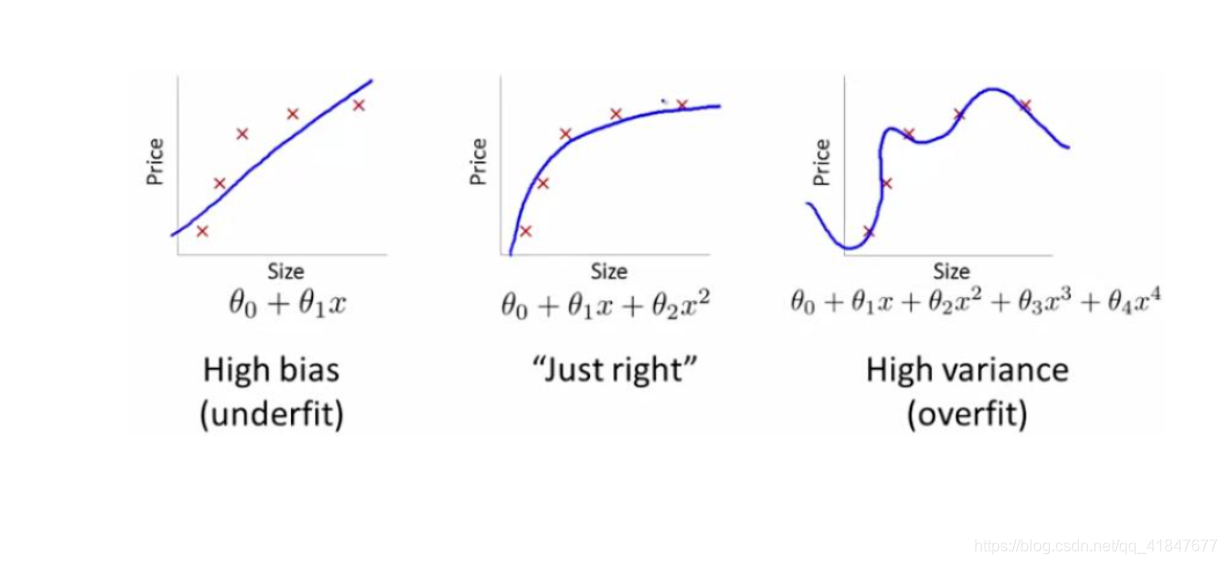
导致结果不正确。

解决办法

使\(\theta\)的取值尽量小，已达到曲线平滑。
但当\(\theta\)取值过小会导致欠拟合
改变代价函数
线性回归：
\[J(\theta)=\frac{1}{2m}(\sum_{i=1}^{m}({h_\theta(x^i)-y(x^i)})^2+\lambda\sum_{j=1}^n\theta_j^2)\]
使用梯度下降迭代
\[\theta_0=\theta_0-\alpha\frac1m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}\]
\[\theta_j=\theta_j-\alpha[\frac1m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+\frac\lambda m\theta_j]\]
\(\theta_j变形\)
\[\theta_j=\theta_j(1-\frac\lambda m\theta_j)-\alpha\frac1m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\]

使用正则化公式
\[ \theta=\left(X^TX+\lambda \left[ \begin{matrix} 0 \\ & 1 \\& &1\\ &&&\ddots\\&&&&1 \end{matrix} \right] \right)^{-1}X^Ty\]

其中
\[X=\begin{bmatrix} x(1)^T\\x(2)^T\\\vdots\\x(m)^T \end{bmatrix} ,y=\begin{bmatrix} y(1) \\y(2) \\\vdots\\y(m) \\\end{bmatrix}\]
\[X为m*(n+1)的矩阵，y为m维向量\]
logistic回归：
与线性回归相同，但是\(h_\theta(X)\)定义不同。

正则化

标签：lin   取值   matrix   sha   strong   term   span   矩阵   sdn   

原文地址：https://www.cnblogs.com/Kseven77/p/12019361.html