标签:石子合并 合并石子 合并类动态规划 合并dp 区间dp
问题描述
设有N堆沙子排成一排,其编号为1,2,3,…,N(N<=100)。每堆沙子有一定的数量。现要将N堆沙子并成为一堆。归并的过程只能每次将相邻的两堆沙子堆成一堆,这样经过N-1次归并后成为一堆。找出一种合理的归并方法,使总的代价最小。
【输入格式】
输入由若干行组成,第一行有一个整数,n(1≤n≤100);表示沙子堆数。第2至m+1行是每堆沙子的数量。
【输出格式】
一个整数,归并的最小代价。
【输入样例】
输入文件名:shizi.in
7
13
7
8
16
21
4
18
【输出样例】
输出文件名:shizi.out
239
矩阵连乘与这类问题非常相似。矩阵连乘每次也是合并相邻两个矩阵(只是计算方式不同)。那么石子合并问题可用矩阵连乘的方法来解决。
那么最优子结构是什么呢?如果有N堆,第一次操作肯定是从n-1个对中选取一对进行合并,第二次从n-2对中选取一对进行合并,以此类推……
求出w的前缀和s,s[0]设为0,s[i]表示w[1]+w[2]+...+w[i],这样的话w[i]+w[i+1]+...+w[j]就是s[j]-s[i-1].
f[i][j]表示从第i堆合并到第j堆的最小代价,则f[i][j] = min(f[i][k]+f[k+1][j]+s[j]-s[i-1])(i<=k<j),f[i][j]初始设置为
INT_MAX.
三层循环,最外层枚举一串合并的长度len,最小是2堆石子合并,最大是n堆.
然后枚举i,那么j就是i+len-1,在i和j之间枚举破点k,比较.
DP 过程:
阶段:以归并石子的长度为阶段,一共有n-1个阶段。
#include <iostream>
using namespace std;
#define M 101
#define INF 1000000000
int n,f[M][M],sum[M][M],stone[M];
int main()
{
int i,j,k,t;
cin>>n;
for(i=1;i<=n;i++)
scanf("%d",&stone[i]);
for(i=1;i<=n;i++)
{
f[i][i]=0;
sum[i][i]=stone[i];
for(j=i+1;j<=n;j++)
sum[i][j]=sum[i][j-1]+stone[j];
}
for(int len=2;len<=n;len++)//归并的石子长度
{
for(i=1;i<=n-len+1;i++)//i为起点,j为终点
{
j=i+len-1; //由于len,表示有len个石子进行归并,从i开始,由于只有相邻的石子才能合并,所以结束位置j=i+len-1
f[i][j]=INF; //初始值都置为无穷大
for(k=i;k<=j-1;k++) //中间断开位置,查找在[i,j]什么位置设置断点k,f[i][j]取最优值
{
if(f[i][j]>f[i][k]+f[k+1][j]+sum[i][j])
f[i][j]=f[i][k]+f[k+1][j]+sum[i][j];
}
}
}
printf("%d/n",f[1][n]);
return 0;
}
在一个圆形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 试设计出1个算法,计算出将N堆石子合并成1堆的最小得分和最大得分.
数据的第1行试正整数N,1≤N≤100,表示有N堆石子.第2行有N个数,分别表示每堆石子的个数.
输出共2行,第1行为最小得分,第2行为最大得分
4
4 4 5 9
43
54
hzoi
递推公式如下:
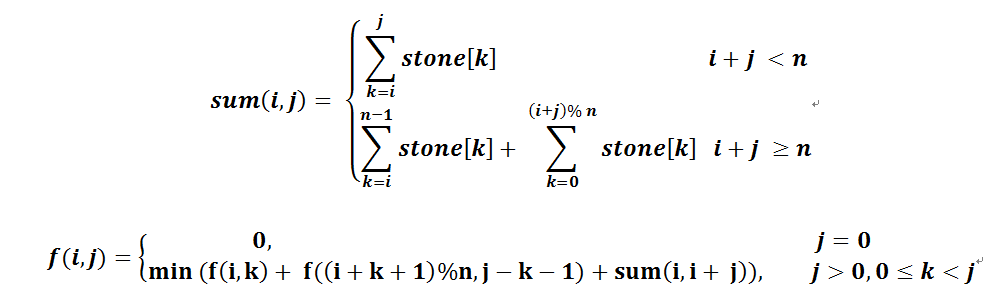
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define MAXN 100
int sum[MAXN];
int mins[MAXN][MAXN], maxs[MAXN][MAXN];
int INT_MAX=999999999;
int n, stone[MAXN];
int sums(int i, int j) {
if(i + j >= n) {
return sums(i, n - i - 1) + sums(0, (i + j) % n);
} else {
return sum[i + j] - (i > 0 ? sum[i - 1] : 0);
}
}
void getBest(int& minnum, int& maxnum) {
//初始化,没有合并,花费为0
for(int i = 0; i < n; ++i) {
mins[i][0] = maxs[i][0] = 0;
}
//还需进行合并次数
for(int j = 1; j < n; ++j) {
for(int i = 0; i < n; ++i) {
mins[i][j] = INT_MAX;
maxs[i][j] = 0;
for(int k = 0; k < j; ++k) {
mins[i][j] = min(mins[i][k] + mins[(i + k + 1)%n][j - k - 1] + sums(i, j), mins[i][j]);
maxs[i][j] = max(maxs[i][k] + maxs[(i + k + 1)%n][j - k - 1] + sums(i, j), maxs[i][j]);
}
}
}
minnum = mins[0][n - 1];
maxnum = maxs[0][n - 1];
for(int i = 0; i < n; ++i) {
minnum = min(minnum, mins[i][n - 1]);
maxnum = max(maxnum, maxs[i][n - 1]);
}
}
int main() {
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%d", &stone[i]);
sum[0] = stone[0];
for(int i = 1; i < n; ++i) {
sum[i] = sum[i - 1] + stone[i];
}
int minnum, maxnum;
getBest(minnum, maxnum);
printf("%d/n%d/n", minnum, maxnum);
return 0;
}环形DP解题思路2:
对于线性的合并石子问题,dp模型类似于“加括号”那类型的dp题目,设 f(i, j)为 将第i项到第j项合并得到的最优解
关键是,这题目是环形的。环形结构,经常采用双倍长度线性化手段,也就是说,把环形结构看成是长度为环的两倍的线性结构来处理。
环的长度是N,所以题目相当于有一排石子1....N+1....N,然后就可以用线性的石子合并问题的方法做了。
有个要注意的地方,f(i, j) 总是与 f(N +i, N +j) 相等的,所以可以减少一些不必要的计算。
此题的关键在于化环为线性结构,与N个数围成一圈,连续多少个数的最大和,异曲同工。
将N结构的线性表,转换为双倍长度的2N结构的线性表,然后在2N长度的表中,截取我们需要的长度为N的部分就可以了。
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <limits.h>
using namespace std;
int dpx[1100][110],p[1100][1100],s[1100],dp[1100][1100];
int anx,any;
int main()
{
int n;
while(cin>>n)
{
memset(p,0,sizeof(p));
for(int i=1;i<=n;i++)
{
cin>>s[i];
s[n+i]=s[i];
}
for(int i=1;i<=2*n;i++)
{
p[i][i]=s[i];
for(int j=i+1;j<=2*n;j++)
p[i][j]=p[i][j-1]+s[j];
}
memset(dp,0,sizeof(dp));
for(int r=1;r<n;r++) //r 表示待合并进来的石子个数
{
for(int i=1;i<=2*n-r;i++) //i表示合并石子,起始位置
{
int j=r+i; //j表示要合并r个石子,合并序列结束的位置
dpx[i][j]=INT_MAX; //初始化
for(int k=i;k<j;k++)
{
dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+p[i][j]);
dpx[i][j]=min(dpx[i][j],dpx[i][k]+dpx[k+1][j]+p[i][j]);
}
}
}
anx=0;
any=INT_MAX;
for(int i=1;i<=n;i++) //2N堆中,求解所有长度为N的连续序列合并最大,最小值
{
anx=max(anx,dp[i][n+i-1]);
any=min(any,dpx[i][n+i-1]);
}
printf("%d\n",any);
printf("%d\n",anx);
}
return 0;
}
标签:石子合并 合并石子 合并类动态规划 合并dp 区间dp
原文地址:http://blog.csdn.net/txl199106/article/details/40620957