标签：机器学习实战 info start 元类 数据 logistic 介绍 科学 isp
本篇随笔是数据科学家学习第六周的内容，主要参考资料为：
1.出场率No.1的逻辑回归算法，是怎样“炼成”的？
https://mp.weixin.qq.com/s/xfteESh2bs1PTuO2q39tbQ
2.逻辑回归
3.以及《机器学习实战》
逻辑回归是应用非常广泛的算法。逻辑回归的建模过程体现了数据建模中很重要的思想：对问题划分层次，并利用非线性变换和线性模型的组合，将未知的复杂问题分解为已知的简单问题。
许多问题需要将概率估算值作为输出。可以使用下面两种方式来获取概率：
1."按原样"
2.转换成二元类别。
我们来了解一下如何“按原样”使用概率。假设我们创建一个逻辑回归模型来预测狗在半夜发出叫声的概率。我们将此概率称为：
p(bark | night)
如果逻辑回归模型预测 p(bark | night) 的值为 0.05，那么一年内(365天)，狗的主人应该被惊醒约 18 次：
startled = p(bark | night) * nights 18 ~= 0.05 * 365
在很多情况下，逻辑回归输出将映射到二元分类问题的解决方案，该二元分类问题的目标是正确预测两个可能的标签（例如，“垃圾邮件”或“非垃圾邮件”）中的一个。之后的单元会重点介绍这一内容。
我们需要将逻辑回归模型返回的概率值映射到0和1之间：
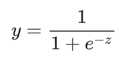S 型函数会产生以下曲线图：
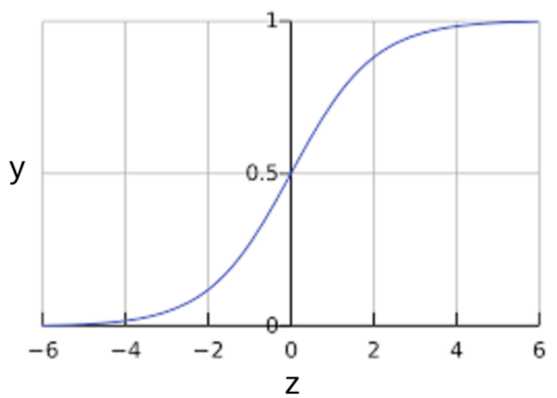
如果Z表示使用逻辑回归训练的模型的线性层的输出，则 S 型(z) 函数会生成一个介于 0 和 1 之间的值（概率）。用数学方法表示为：
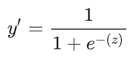
其中：
请注意，z 也称为对数几率，因为 S 型函数的反函数表明，z 可定义为标签“1”（例如“狗叫”）的概率除以标签“0”（例如“狗不叫”）的概率得出的值的对数：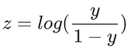
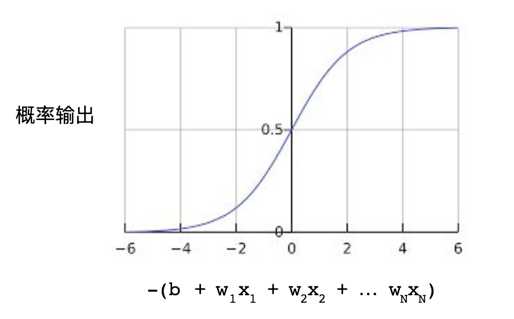
以下是具有机器学习标签的 S 型函数：
TODO
TODO
TODO
标签：机器学习实战 info start 元类 数据 logistic 介绍 科学 isp
原文地址：https://www.cnblogs.com/favor-dfn/p/12038741.html
