标签:存在 ret img color 奇数 时间 ima lld sig
连续打了3场$codeforces$,深深的被各种模拟贪心分类讨论的$C$,$D$题给恶心到了
还有永远看到题一脸懵的$B$题
首先考虑画出不同函数值迭代转移的关系,要注意考虑连边是否能成立,也就是满不满足函数的定义域
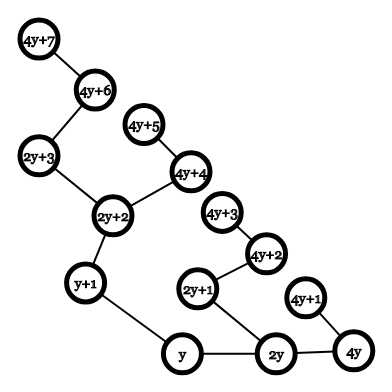
首先观察上图,可以发现如果$y$是偶数,节点$y$的左子树存在
但如果$y$是奇数,节点$y$的左子树不存在,因为$y+1$是偶数,不满足$f(x)=x-1$的定义域
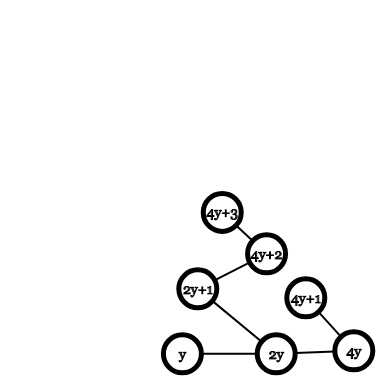
并且右子树的所有节点都存在,因为都是奇数,如下图
那么现在统计一个定值$y$在$1-n$中经过$y$的$path$数,就是以y为根这棵树结点值小于等于n的节点数
观察可以发现,这些节点的值有规律
对于$2^{k}y$级别,树上的范围为$2^{k}y$到$2^{k}y+2^{k+1}-1$
那么可以在$log$的时间求出来
奇数的也是同理,$2^{k}y$到$2^{k}y+2^{k}-1$
但题目要求的是最大的$y$
那么可以分奇数偶数分别二分求解

1 #include <bits/stdc++.h> 2 #define ll unsigned long long 3 #define inf (int)1e9 4 #define m_k make_pair 5 using namespace std; 6 ll n,k,z[63],ans; 7 bool check(ll mid) 8 { 9 if (mid==1) 10 return 1; 11 ll cnt=0; 12 if (mid%2==1) 13 { 14 for (int i=0;i<=62;i++) 15 { 16 if (z[i]*mid>n) 17 break; 18 if (z[i]*mid+z[i]-1<n) 19 cnt+=z[i]; 20 else 21 { 22 cnt+=n-z[i]*mid+1; 23 break; 24 } 25 } 26 } 27 else 28 { 29 for (int i=0;i<=62;i++) 30 { 31 if (z[i]*mid>n) 32 break; 33 if (z[i]*mid+z[i+1]-1<n) 34 cnt+=z[i+1]; 35 else 36 { 37 cnt+=n-z[i]*mid+1; 38 break; 39 } 40 } 41 } 42 if (cnt>=k) 43 return 1; 44 else 45 return 0; 46 } 47 int main() 48 { 49 scanf("%lld%lld",&n,&k); 50 if (k==n) 51 { 52 printf("1\n"); 53 return 0; 54 } 55 z[0]=1; 56 for (int i=1;i<=62;i++) 57 z[i]=z[i-1]*2; 58 ll l,r; 59 l=0;r=(n-1)/2; 60 while (l<r) 61 { 62 ll mid=l+((r-l+1)>>1); 63 if (check(2*mid+1)) 64 l=mid; 65 else 66 r=mid-1; 67 } 68 ans=2*l+1; 69 l=0;r=n/2; 70 while (l<r) 71 { 72 ll mid=l+((r-l+1)>>1); 73 if (check(2*mid)) 74 l=mid; 75 else 76 r=mid-1; 77 } 78 ans=max(ans,2*l); 79 printf("%lld\n",ans); 80 }
标签:存在 ret img color 奇数 时间 ima lld sig
原文地址:https://www.cnblogs.com/huangchenyan/p/12045964.html