LeetCode 第53题，最大子序和

标签：sub   图片   cto   subarray   src   分治   来源   arrays   jpg   

题目概述

• 题目：力扣：53.最大子序和
• 难易：简单
• 内容：

  给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  示例:

  输入: [-2,1,-3,4,-1,2,1,-5,4]

  输出: 6

  解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

  来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/maximum-subarray

第一次思路

首先将数组类型分为三类：1.空数组 2.只有一个元素 3. 多个元素

1. 空数组：返回0；
2. 只有一个元素：最大子序和即为他本身
3. 多个元素：
   ①. 将第一个元素记为和（sum）和最大的和(max)
   ②. 如果和大于0，则继续加上下一位数字，如果和小于零就将sum赋值为下一位数字
   ③. max保存的是到当前元素为止最大的子序和

Code

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum=nums[0];
            int max=nums[0];
        if(nums.size()==0)
            return 0;
        else if(nums.size()==1)
            return nums[0];
        else{
            
            for(int i(1);i<nums.size();i++){
                if(sum>0)
                    sum+=nums[i];
                else 
                    sum=nums[i];
                if(max<sum)
                    max=sum;
            
            }
           
        }
      return max;   
    }

};

测试 Submit

分析

在LeetCode分析中发现一个很有趣的描述为赌徒，下图为LeetCode的截图

改进

分治法
其实就是它的最大子序和有三种可能。在左半边，在右半边，第三种是穿过中间。对于左右边的序列，情况一样，因此可以用递归处理。中间部分的则可以直接计算出来。

改进Code

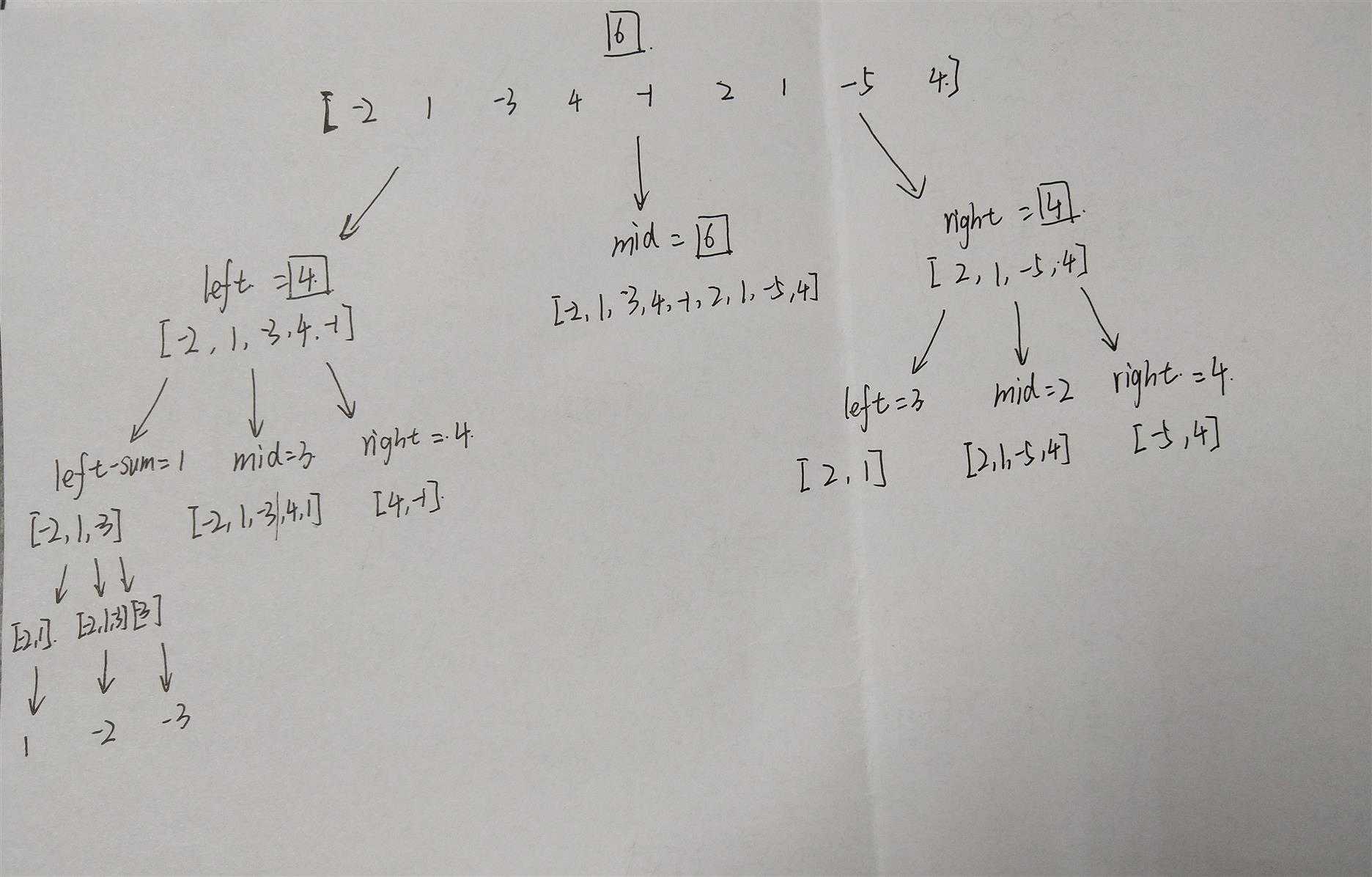
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result=INT_MIN;
        result = maxSubArraySum(nums,0,nums.size()-1);
        return result;
    }
    int maxSubArraySum(vector<int>& nums,int left,int right){
        if(left==right){
            return nums[left];
        }
        int mid = (left+right)/2;
        int leftSum = maxSubArraySum(nums,left,mid);
        int rightSum = maxSubArraySum(nums,mid+1,right);
        int midSum = midmaxSubArraySum(nums,left,mid,right);
        int result = max(leftSum,rightSum);
        result = max(result,midSum);
        return result;
    }
    int midmaxSubArraySum(vector<int>& nums,int left,int mid,int right){
        int sum=0;
        int leftSum=INT_MIN;
        int rightSum=INT_MIN;
        for(int i=mid;i>=left;i--){
            sum = sum+nums[i];
            leftSum = max(sum,leftSum);
        }
        sum=0;
        for(int i=mid+1;i<=right;i++){
            sum = sum+nums[i];
            rightSum = max(sum,rightSum);
        }
        return (leftSum+rightSum);
    }
};

改进Submit

收获总结

分治法是真的难理解啊啊啊啊啊！！！

LeetCode 第53题，最大子序和

标签：sub   图片   cto   subarray   src   分治   来源   arrays   jpg   

原文地址：https://www.cnblogs.com/HanLongfeng/p/12050031.html