标签：直接   向量   相加   观测   机器学习   认知   问题   因此   数学   

前言：学习机器学习的过程意识到，数学是工科的基石。很多数学公式似懂非懂，因此有了这篇博客，想在学习每个模型的过程中搞懂其中的数学理论。

贝叶斯决策论

1.前置知识：先验概率与后验概率

• 先验概率P(B)：根据以往经验和分析得到的概率

　　先验概率是一种常识性、经验性认知，比如抛硬币正反面的概率是1/2。

• 后验概率P(A|B)：某个因素的到来影响了对某个结果发生可能性的判断

　　后验概率是基于已知，对结果发生的可能性一种推测。

比如：文本分类中，假设文章类别为3类，没有数据时，观测到类别c的概率是先验概率P(c),数据x的到来改变这个概率为P(c|x)，是数据支持这个类发生的可能性，以此作为数据所属类别。这就是后验概率。

2.贝叶斯分类器

• 2.1.贝叶斯公式：

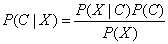　　（公式1）

　　其中，P（C|X）是根据样本X对类别C的预测值。P(C)是类先验概率，它表示为某类样本在总样本中出现的可能性，对于某个样本，P(X)与样本分类无关。因此，求贝叶斯公式的关键在于求类条件概率P(X|C)。

• 2.2.对数极大似然估计

　　似然即类条件概率P(X|C)，假设P(X|C)被参数向量θ_c唯一确定，则参数θ_c对数据样本某类类别为C的训练样本D_c的似然可以表示为：

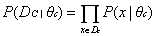　　　（公式2）

 　　对θ_c进行极大似然估计，就是去寻找最大化似然P(D_c|θ_c)的参数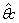。在文本分类的实际问题中，表现为寻找一个最可能使数据D_c出现的类别，即：为数据D_c找到最可能的分类。

 　　在公式2中，因为每个文本类别的属性值往往有多个，这种连乘操作容易造成下溢，因此需要估计对数似然：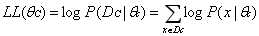

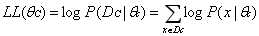　　(公式3)

 　　此时，多个属性的连乘就通过对数函数表现为相加。

 　　此时，对参数θ_c的极大似然估计表现为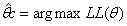：　（公式4）

• 2.3.朴素贝叶斯分类器

　　在实际分类问题中，样本的属性有可能是互相关联的，比如：x₁的出现有可能会影响到x₂的出现。对于类条件概率P(X|C),它涉及X中所有属性的联合概率，直接根据样本频率去估计，假设有d个属性，假设每个属性有n种可能取值，样本空间则有n^d种排列，远远大于训练样本数。难以从有限样中估计得到。

　　朴素贝叶斯分类器的“朴素”之处在于：假设这些属性都是独立的。即每个属性都独立的对结果造成影响。基于这种思想，贝叶斯公式可以改写为：

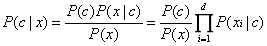　　（公式5）

 　　对于所有类别来说，P(x)相同，不起作用。所以，朴素贝叶斯公式的准则可以进一步表达为：

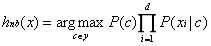　　（公式6）

 　　其中，h_nb(x)为错误率，它就等于最大化似然。

3.朴素贝叶斯文本分类

在文本分类中，各成员的实际意义表示为：

，

 此时有一个问题：假设测试样本中某个单词在训练样本中没有出现过，那么似然估计结果为0，会导致估计错误。因此需要对数据做拉普拉斯平滑处理。处理过程如下：

，

这样就有效解决了某个出现新词语导致的连乘结果为0的问题。

基于朴素贝叶斯的文本分类

标签：直接   向量   相加   观测   机器学习   认知   问题   因此   数学   

原文地址：https://www.cnblogs.com/yanglive/p/12050611.html