标签:iter 作业 pyplot 向量 code load 一个 flat 导致
前言:今天从早上开始写吴恩达多层神经网络的题目。反复运算,出现一个天坑,一个存储矩阵的字典parameters的W1和b1在传入函数updata_parameters前维数还是(7, 12288), 传进去后变成了(3, 4)导致不能和grads["dW1"]的维数(7, 12288)进行广播出错。调了半天也不知道到底哪里出错了。最后重新写了一遍没有出错。
神经网络训练过程:
1.初始化参数
2.进行前向传播(其中分两部分,一部分是前向传播的计算部分,另一部分是前向传播的激活部分)
3.计算损失
4.进行后向传播(同样分为两部分,一部分是后向传播的计算部分,另一部分是后向传播的激活部分)
5.更新参数,整合模型,进行预测
1.初始化参数
首先导入需要用到的包。我们先做只有两层的神经网络。
1 import numpy as np 2 import h5py 3 import matplotlib.pyplot as plt 4 import testCase 5 from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward 6 import lr_utils 7 8 9 plt.rcParams[‘figure.figsize‘] = (5.0, 4.0); 10 plt.rcParams[‘image.interpolation‘] = ‘nearest‘; 11 plt.rcParams[‘image.cmap‘] = ‘gray‘; 12 13 14 np.random.seed(1);#初始化随机种子
进行参数的初始化。
1 def initialize_parameters(n_x, n_h, n_y):#因为只有两层,所以只有输入层数量n_x,隐藏层数量n_h,输出层数量n_y 2 np.random.seed(1); 3 4 W1 = np.random.randn(n_h, n_x) * 0.01; 5 b1 = np.zeros((n_h, 1)); 6 W2 = np.random.randn(n_y, n_h) * 0.01; 7 b2 = np.zeros((n_y, 1)); 8 9 assert(W1.shape == (n_h, n_x)); 10 assert(b1.shape == (n_h, 1)); 11 assert(W2.shape == (n_y, n_h)); 12 assert(b2.shape == (n_y, 1)); 13 14 parameters = {"W1": W1, 15 "b1": b1, 16 "W2": W2, 17 "b2": b2}; 18 19 return parameters;
2.进行前向传播
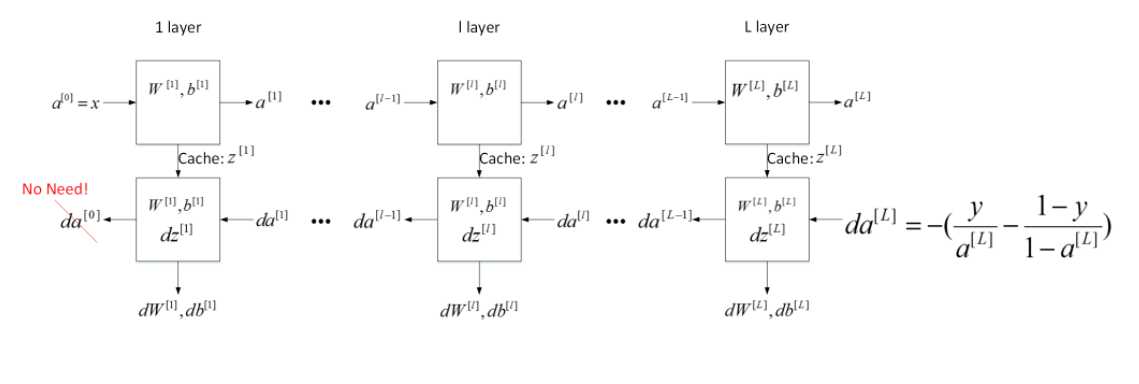
进行前向传播的计算部分,计算Z,需要传入的参数为A,W,b, 并将A,W,b放入缓存cache中,后面需要用到。
1 def linear_forward(A, W, b): 2 3 Z = np.dot(W, A) + b; 4 5 assert(Z.shape == (W.shape[0], A.shape[1])); 6 cache = (A, W, b); 7 8 return Z, cache;
接着计算前向传播的激活部分,需要传入的数据是A_prev(前一层的激活值A),W, b,激活函数的类型activation。
1 def linear_activation_forward(A_prev, W, b, activation): 2 if activation == "sigmoid": 3 Z, linear_cache = linear_forward(A_prev, W, b); # Z, linear_cache中缓存(W, A_prev, B) 4 A, activation_cache = sigmoid(Z); # A, activation_cache中缓存(Z) 5 elif activation == "relu": 6 Z, linear_cache = linear_forward(A_prev, W, b); 7 A, activation_cache = relu(Z); 8 9 assert (A.shape == (W.shape[0], A_prev.shape[1])); 10 cache = (linear_cache, activation_cache); #, ((W, A_prev, B) ,(Z)) 11 12 return A, cache;
3.计算损失
需要传入的参数是最后第L层的激活值AL,和目标向量Y。
1 def compute_cost(AL, Y): 2 m = Y.shape[1]; 3 4 cost = -1 / m * (np.dot(Y, np.log(AL).T) + np.dot(1 - Y, np.log(1 - AL).T)); 5 6 cost = np.squeeze(cost); # 将形状如[[17]]的向量转为形状为17的向量 7 assert(cost.shape == ()); 8 9 return cost;
4.后向传播


先计算后向传播的计算部分。需要的参数是dZ(可以通过dA和Z计算得出), cache中缓存的是(A_prev, W, b)。
1 def linear_backward(dZ, cache): 2 A_prev, W, b = cache; 3 m = A_prev.shape[1]; 4 5 dW = 1 / m * np.dot(dZ, A_prev.T); 6 db = 1 / m * np.sum(dZ, axis = 1, keepdims = True); 7 dA_prev = np.dot(W.T, dZ); 8 9 assert (dA_prev.shape == A_prev.shape); 10 assert (dW.shape == W.shape); 11 assert (db.shape == b.shape); 12 13 return dA_prev, dW, db;
接着计算后向传播的激活部分。需要的参数是dA, cache(有两部分缓存的值,一个是linear_cache,一个是activation_cache), activation。
1 def linear_activation_backward(dA, cache, activation): 2 3 linear_cache, activation_cache = cache 4 5 if activation == "relu": 6 dZ = relu_backward(dA, activation_cache); 7 dA_prev, dW, db = linear_backward(dZ, linear_cache); 8 9 elif activation == "sigmoid": 10 dZ = sigmoid_backward(dA, activation_cache); 11 dA_prev, dW, db = linear_backward(dZ, linear_cache); 12 13 return dA_prev, dW, db;
5.更新参数,整合模型,进行预测
更新参数需要传入的参数有parameters(存储参数W1, b1等的字典), grads(存储梯度的字典), learning_rate。
1 def update_parameters(parameters, grads, learning_rate): 2 L = len(parameters) // 2 #整除2,因为parameters中的参数是按W1,b1,W2,b2排列的 3 for l in range(L): 4 parameters["W" + str(l + 1)] -= learning_rate * grads["dW" + str(l + 1)]; 5 parameters["b" + str(l + 1)] -= learning_rate * grads["db" + str(l + 1)]; 6 return parameters;
传入吴恩达第二周编程作业中的数据集。
1 train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset() 2 3 train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T 4 test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T 5 6 train_x = train_x_flatten / 255 7 train_y = train_set_y 8 test_x = test_x_flatten / 255 9 test_y = test_set_y
整合模型。
1 def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False): 2 3 np.random.seed(1); 4 grads = {}; 5 costs = []; 6 m = X.shape[1]; 7 (n_x, n_h, n_y) = layers_dims; 8 9 parameters = initialize_parameters(n_x, n_h, n_y); 10 11 W1 = parameters["W1"]; 12 b1 = parameters["b1"]; 13 W2 = parameters["W2"]; 14 b2 = parameters["b2"]; 15 16 17 for i in range(0, num_iterations): 18 A1, cache1 = linear_activation_forward(X, W1, b1, "relu"); 19 A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid"); 20 21 cost = compute_cost(A2, Y); 22 23 dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2)); 24 25 dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid"); 26 dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu"); 27 28 grads[‘dW1‘] = dW1; 29 grads[‘db1‘] = db1; 30 grads[‘dW2‘] = dW2; 31 grads[‘db2‘] = db2; 32 33 parameters = update_parameters(parameters, grads, learning_rate); 34 35 W1 = parameters["W1"]; 36 b1 = parameters["b1"]; 37 W2 = parameters["W2"]; 38 b2 = parameters["b2"]; 39 40 if i % 100 == 0: 41 #记录成本 42 costs.append(cost) 43 #是否打印成本值 44 if print_cost: 45 print("第", i ,"次迭代,成本值为:" ,np.squeeze(cost)) 46 47 48 plt.plot(np.squeeze(costs)); 49 plt.ylabel(‘cost‘); 50 plt.xlabel(‘iterations (per tens)‘); 51 plt.title("Learning rate =" + str(learning_rate)); 52 plt.show(); 53 54 return parameters;
整合完成后直接调用该函数就可以进行训练。
1 n_x = 12288
2 n_h = 7
3 n_y = 1
4 parameters = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost = True);
训练结果:

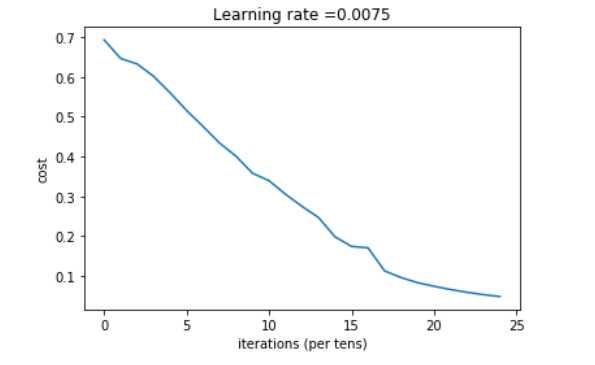
查看一下准确率,需要写一个函数。
1 def predict(X, y, parameters): 2 m = X.shape[1] 3 n = len(parameters) // 2 # 神经网络的层数 4 p = np.zeros((1,m)) 5 6 #根据参数前向传播 7 probas, caches = L_model_forward(X, parameters) 8 9 for i in range(0, probas.shape[1]): 10 if probas[0,i] > 0.5: 11 p[0,i] = 1 12 else: 13 p[0,i] = 0 14 15 print("准确度为: " + str(float(np.sum((p == y))/m))) 16 17 return p
查看准确率。
1 pred_train = predict(train_x, train_y, parameters) #训练集
2 pred_test = predict(test_x, test_y, parameters) #测试集
![]()
相较之前的logistic回归的预测70%有所提高。
标签:iter 作业 pyplot 向量 code load 一个 flat 导致
原文地址:https://www.cnblogs.com/1-0001/p/12057501.html