标签:根据 高度 灵活 思考 block line 图片 图形 abc
利用正余弦定理判断三角形的个数的常用思路:
①代数法:从数的角度思考,根据大边对大角的性质,三角形内角和公式,正弦函数值判断;
②几何图形法,从形的角度思考,根据条件画出图形,通过图形直观判断三角形的个数;
法1:代数法,由\(\cfrac{a}{sinA}=\cfrac{b}{sinB}\),得到\(sinB=\cfrac{\sqrt{3}}{2}\),
故\(B=60^{\circ}\)或\(B=120^{\circ}\),则对应的三角形有两个,故选\(B\);
法2:几何图形法,可仿例3完成,由于\(bsinA=\sqrt{3}\),则\(bsinA<a<b\),
故满足条件的三角形有两个。
法1:从形的角度,如图所示,\(AD=20\sqrt{3}\),当以点\(A\)为圆心,以\(20\)为半径做圆时,
此时和角的另一边\(CD\)没有交点,故满足题意的三角形是不存在的。
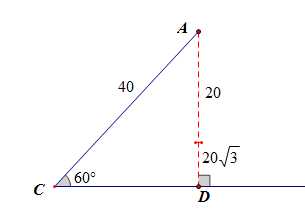
法2:从数的角度,如果这样的三角形是存在的,那么由正弦定理可知,
\(\cfrac{b}{sinB}=\cfrac{c}{sinC}\),得到\(sinB=\cfrac{bsinC}{c}=\sqrt{3}>1\),
我们知道\(|sinx|\leq 1\),故这样的\(B\)不存在,即满足题意的三角形不存在。
分析:这样的题目我们一般是从形的角度入手分析的多见一些,因为毕竟有形的帮助要直观的多。
如图所示,由图像可知\(CD=6\sqrt{3}\),
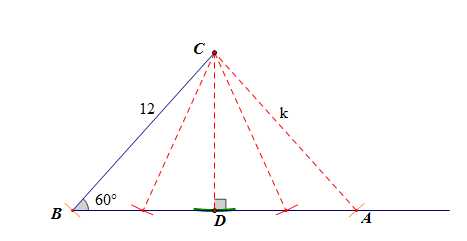
当\(k\in(0,6\sqrt{3})\)时,满足题意的三角形不存在;
当\(k=6\sqrt{3}\)时,满足题意的三角形是唯一的,且是直角三角形。
当\(k\in(6\sqrt{3},12)\)时,满足题意的三角形是两个。
当\(k=12\)时,满足题意的三角形是一个,是等腰三角形。
当\(k>12\)时,满足题意的三角形是一个。
【解后反思】1、学生对这类题目的掌握一般都不太好,不会作图,不会应用图像解决问题。
2、这类题目作图的顺序是这样的,先做出\(\angle B\),一条已知边\(BC\)要么水平放置,要么斜放着,一般都是斜放着,此时点\(C\)就有了着落,这样放置也便于求点\(C\)到下底边上的高,然后以点\(C\)为圆心,以\(AC\)长为半径画弧,若所画的弧与下底边有交点,这个交点就是点\(A\),有几个交点就意味着有几个三角形存在,若所画的弧与下底边没有交点,则这样的三角形是不存在的。
法1:从数的角度入手,由正弦定理\(\cfrac{k}{sinA}=\cfrac{12}{sin60^{\circ}}\),
得到方程\(k=8\sqrt{3}sinA,A\in(0,\cfrac{2\pi}{3})\)有一个解,或者两个函数图像有一个交点,数形结合求解即可。
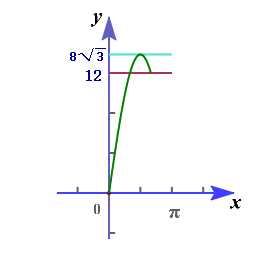
由图可知,满足题意的三角形恰有一个,则\(k\in(0,12]\)或\(k=8\sqrt{3}\)。
法2:从形的角度入手,动静元素互换位,即让长为12的边变化,让长为\(k\)的边不变化。
如图,以点C为圆心画弧,当12小于点C到边AB的高度\(k\cdot\cfrac{\sqrt{3}}{2}\)时 此时三角形是不存在的,
即\(k\cfrac{\sqrt{3}}{2}>12\)时,解得\(k>8\sqrt{3}\);
当12等于点C到边AB的高度\(k\cfrac{\sqrt{3}}{2}\)时,三角形是唯一的,
即\(12=k\cfrac{\sqrt{3}}{2}\),解得\(k=8\sqrt{3}\);
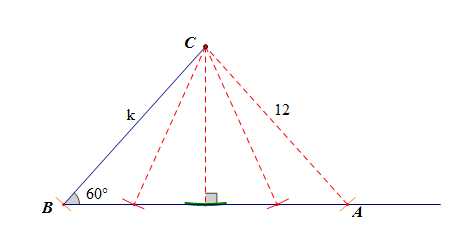
当\(12\)大于点\(C\)到边\(AB\)的高度\(k\cdot\cfrac{\sqrt{3}}{2}\)时,三角形是两个的,
即\(12>k\cdot\cfrac{\sqrt{3}}{2}\),解得\(k<8\sqrt{3}\);
当\(12\)大于或等于边\(BC\)时,三角形是唯一的,即\(12\ge k>0\),
综上可知,当\(k=8\sqrt{3}\)或\(k\in(0,12]\)时,满足条件的三角形恰好只有一个。
【解后反思】1、动静互换,体现了思维的灵活性;
2、是否可以这样想,有一种从形入手分析的思路,必然就会有一种从数入手的思路与之对应。
标签:根据 高度 灵活 思考 block line 图片 图形 abc
原文地址:https://www.cnblogs.com/wanghai0666/p/12058516.html