标签:date() 分析 leo 形状 similar github 不用 counter binary
Solver类用于网络参数的更新,而SGDSolver类实现了优化方法中的随机梯度下降法(stochastic gradient descent),此外还具备缩放、正则化梯度等功能。caffe中其他的优化方法都是SGDSolver类的派生类,重载了基类的ComputeUpdateValue()函数,用于各自计算更新的梯度。
// Return the current learning rate. The currently implemented learning rate
// policies are as follows:
// - fixed: always return base_lr.
// - step: return base_lr * gamma ^ (floor(iter / step))
// - exp: return base_lr * gamma ^ iter
// - inv: return base_lr * (1 + gamma * iter) ^ (- power)
// - multistep: similar to step but it allows non uniform steps defined by
// stepvalue
// - poly: the effective learning rate follows a polynomial decay, to be
// zero by the max_iter. return base_lr (1 - iter/max_iter) ^ (power)
// - sigmoid: the effective learning rate follows a sigmod decay
// return base_lr ( 1/(1 + exp(-gamma * (iter - stepsize))))
//
// where base_lr, max_iter, gamma, step, stepvalue and power are defined
// in the solver parameter protocol buffer, and iter is the current iteration.
template <typename Dtype>
Dtype SGDSolver<Dtype>::GetLearningRate() { //根据当前的迭代次数和学习率的更新策略计算并返回当前的学习率
Dtype rate;
const string& lr_policy = this->param_.lr_policy(); //获取学习率的更新策略
if (lr_policy == "fixed") { //每次迭代的学习率为固定值
rate = this->param_.base_lr();
} else if (lr_policy == "step") { //每隔stepsize_次,当前的学习率乘上系数gamma_
CHECK_GT(this->param_.stepsize(), 0);
this->current_step_ = this->iter_ / this->param_.stepsize(); //current_step_为int类型,为当前阶数
CHECK_GE(this->param_.gamma(), 0);
rate = this->param_.base_lr() * pow(this->param_.gamma(), this->current_step_); //lr = base_lr_ * (gamma_ ^ current_step_)
} else if (lr_policy == "exp") { //每次迭代,当前的学习率乘上系数gamma_
CHECK_GE(this->param_.gamma(), 0);
rate = this->param_.base_lr() * pow(this->param_.gamma(), this->iter_); //lr = base_lr_ * (gamma_ ^ iter_)
} else if (lr_policy == "inv") { //计算公式: lr = base_lr_ * (1 + gamma_ * iter_) ^ (-power_)
CHECK_GE(this->param_.gamma(), 0);
rate = this->param_.base_lr() * pow(Dtype(1) + this->param_.gamma() * this->iter_, - this->param_.power());
} else if (lr_policy == "multistep") {
//stepvalue_中保存了每个阶段需要的迭代次数,stepvalue_[0] stepvalue_[1] stepvalue_[2] ...
//当前迭代次数每递增到一个新的stepvalue_[n]时,当前的学习率乘上系数gamma_
if (this->current_step_ < this->param_.stepvalue_size() &&
this->iter_ >= this->param_.stepvalue(this->current_step_)) { //迭代次数递增到stepvalue_[n]
this->current_step_++; //进入下一阶段
LOG(INFO) << "MultiStep Status: Iteration " <<
this->iter_ << ", step = " << this->current_step_;
}
CHECK_GE(this->param_.gamma(), 0);
rate = this->param_.base_lr() * pow(this->param_.gamma(), this->current_step_);
} else if (lr_policy == "poly") { //计算公式: lr = base_lr_ * (1 - iter_ / max_iter_) ^ power_
rate = this->param_.base_lr() * pow(Dtype(1.) -
(Dtype(this->iter_) / Dtype(this->param_.max_iter())), this->param_.power());
} else if (lr_policy == "sigmoid") { //计算公式: lr = base_lr_ * (1 / (1 + exp(-gamma_ * (iter_ - stepsize_))))
CHECK_GE(this->param_.gamma(), 0); //检查参数的范围, gamma_ >= 0, stepsize_ > 0
CHECK_GT(this->param_.stepsize(), 0);
rate = this->param_.base_lr() * (Dtype(1.) /
(Dtype(1.) + exp(-this->param_.gamma() * (Dtype(this->iter_) - Dtype(this->param_.stepsize())))));
} else {
LOG(FATAL) << "Unknown learning rate policy: " << lr_policy;
}
return rate;
}
//求解器求解之前的预处理操作,清空求解器内部数据,并根据网络的各个可学习参数blob的大小创建新的空blob
template <typename Dtype>
void SGDSolver<Dtype>::PreSolve() {
// Initialize the history
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //网络中所有可学习参数
history_.clear(); //清空历史梯度数据,更新数据,临时数据
update_.clear(); //三个数据的形状均与参数blob的形状一致
temp_.clear();
for (int i = 0; i < net_params.size(); ++i) {
const vector<int>& shape = net_params[i]->shape(); //第i个可学习参数blob的形状
history_.push_back(shared_ptr<Blob<Dtype> >(new Blob<Dtype>(shape))); //使用该形状创建空blob,保存指针
update_.push_back(shared_ptr<Blob<Dtype> >(new Blob<Dtype>(shape)));
temp_.push_back(shared_ptr<Blob<Dtype> >(new Blob<Dtype>(shape)));
}
}
//裁剪梯度,参数的梯度数据的l2范数值不能超过设定值clip_gradients,否则会缩放梯度数据
template <typename Dtype>
void SGDSolver<Dtype>::ClipGradients() {
const Dtype clip_gradients = this->param_.clip_gradients(); //设定的裁剪的阈值
if (clip_gradients < 0) { return; } //设定值大于0才有效,默认-1
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //网络中所有可学习参数
Dtype sumsq_diff = 0;
for (int i = 0; i < net_params.size(); ++i) {
sumsq_diff += net_params[i]->sumsq_diff(); //累加所有参数blob的梯度数据diff_的平方和
}
const Dtype l2norm_diff = std::sqrt(sumsq_diff); //参数梯度的l2范数
if (l2norm_diff > clip_gradients) { //大于设定值
Dtype scale_factor = clip_gradients / l2norm_diff; //缩放系数
LOG(INFO) << "Gradient clipping: scaling down gradients (L2 norm "
<< l2norm_diff << " > " << clip_gradients << ") "
<< "by scale factor " << scale_factor; //打印信息
for (int i = 0; i < net_params.size(); ++i) {
net_params[i]->scale_diff(scale_factor); //缩放所有参数blob的梯度数据
}
}
}
//根据参数的梯度,网络的学习率和权重衰减等计算实际更新时的梯度,并更新网络中的所有可学习参数
template <typename Dtype>
void SGDSolver<Dtype>::ApplyUpdate() {
Dtype rate = GetLearningRate(); //获取当前的学习率
if (this->param_.display() && this->iter_ % this->param_.display() == 0) { //设置了打印,并且当前迭代次数需要显示打印信息
LOG_IF(INFO, Caffe::root_solver()) << "Iteration " << this->iter_
<< ", lr = " << rate;
}
ClipGradients(); //裁剪梯度,缩放网络中所有可学习参数的梯度
for (int param_id = 0; param_id < this->net_->learnable_params().size(); ++param_id) {
Normalize(param_id); //将参数的梯度缩小iter_size倍,得到单次迭代时可学习参数的平均梯度
Regularize(param_id); //施加l1或l2正则化,衰减参数的梯度
//其他梯度更新的方法都继承于SGDSolver类,都实现了各自的ComputeUpdateValue()函数,确定了用于参数更新的梯度值
ComputeUpdateValue(param_id, rate); //根据冲量,学习率参数和历史梯度值更新当前的梯度值
}
this->net_->Update(); //使用计算后的梯度值更新网络中的所有可学习参数, data_ = Dtype(-1) * diff_ + data_
// Increment the internal iter_ counter -- its value should always indicate
// the number of times the weights have been updated.
++this->iter_;
}
//将net中的第param_id个可学习参数的梯度数据缩小 1/iter_size 倍
//单次迭代会执行iter_size次的前向和反向过程,每次反向过程都会累加梯度,所以需要先缩小
template <typename Dtype>
void SGDSolver<Dtype>::Normalize(int param_id) {
if (this->param_.iter_size() == 1) { return; } //iter_size=1就不用此操作了
// Scale gradient to counterbalance accumulation.
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //所有可学习参数
const Dtype accum_normalization = Dtype(1.) / this->param_.iter_size(); // 1/iter_size
switch (Caffe::mode()) {
case Caffe::CPU: { //cpu模式下,net_params[param_id]的diff_数据全部乘上系数 1/iter_size
caffe_scal(net_params[param_id]->count(), accum_normalization,
net_params[param_id]->mutable_cpu_diff());
break;
}
case Caffe::GPU: { //同理,gpu模式下所有参数的diff_也都乘上系数
#ifndef CPU_ONLY
caffe_gpu_scal(net_params[param_id]->count(), accum_normalization,
net_params[param_id]->mutable_gpu_diff());
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
//将网络中的第param_id个参数blob进行l1或l2正则化
template <typename Dtype>
void SGDSolver<Dtype>::Regularize(int param_id) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //所有可学习参数
const vector<float>& net_params_weight_decay =
this->net_->params_weight_decay(); //所有可学习参数对应的权重衰减系数
Dtype weight_decay = this->param_.weight_decay(); //求解器参数中设置的基础权重衰减值
string regularization_type = this->param_.regularization_type(); //求解器参数中设置的正则化类型
Dtype local_decay = weight_decay * net_params_weight_decay[param_id]; //该参数对应的权重衰减值
switch (Caffe::mode()) {
case Caffe::CPU: {
if (local_decay) { //非0
if (regularization_type == "L2") { //l2正则化
// add weight decay
//L2正则化会在损失函数中增加项 1/2 * λ * θ^2, 因此计算参数的梯度时,每个参数的梯度会增加项 λ * θ
//θ对应参数的data_数据, λ对应参数的权重衰减值local_decay
caffe_axpy(net_params[param_id]->count(),
local_decay,
net_params[param_id]->cpu_data(),
net_params[param_id]->mutable_cpu_diff()); //公式 diff_ += local_decay * data_
} else if (regularization_type == "L1") {
//l1正则化会在损失函数中增加 λ * |θ|, 对应参数的梯度增加 λ * sign(θ). sign(θ)表示参数θ的符号,正(1),负(-1)
caffe_cpu_sign(net_params[param_id]->count(),
net_params[param_id]->cpu_data(),
temp_[param_id]->mutable_cpu_data()); //判断data_中数据的符号,结果存在临时变量temp_的data_中
caffe_axpy(net_params[param_id]->count(),
local_decay,
temp_[param_id]->cpu_data(),
net_params[param_id]->mutable_cpu_diff()); //公式 diff_ += local_decay * sign(data_)
} else {
LOG(FATAL) << "Unknown regularization type: " << regularization_type;
}
}
break;
}
case Caffe::GPU: { //以下操作同理,在gpu上实现
#ifndef CPU_ONLY
if (local_decay) {
if (regularization_type == "L2") {
// add weight decay
caffe_gpu_axpy(net_params[param_id]->count(),
local_decay,
net_params[param_id]->gpu_data(),
net_params[param_id]->mutable_gpu_diff()); // diff_ += local_decay * data_
} else if (regularization_type == "L1") {
caffe_gpu_sign(net_params[param_id]->count(),
net_params[param_id]->gpu_data(),
temp_[param_id]->mutable_gpu_data()); //temp_data_ = sign(data_)
caffe_gpu_axpy(net_params[param_id]->count(),
local_decay,
temp_[param_id]->gpu_data(),
net_params[param_id]->mutable_gpu_diff()); //diff_ += local_decay * sign(data_)
} else {
LOG(FATAL) << "Unknown regularization type: " << regularization_type;
}
}
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
#ifndef CPU_ONLY
template <typename Dtype>
void sgd_update_gpu(int N, Dtype* g, Dtype* h, Dtype momentum,
Dtype local_rate); //该函数定义在 sgd_solver.cu 文件中
#endif
//根据冲量参数,学习率参数和历史梯度数据,更新当前的梯度值
template <typename Dtype>
void SGDSolver<Dtype>::ComputeUpdateValue(int param_id, Dtype rate) {
const vector<Blob<Dtype>*>& net_params = this->net_->learnable_params(); //网络中所有参数blob
const vector<float>& net_params_lr = this->net_->params_lr(); //每个参数对应的学习率系数
Dtype momentum = this->param_.momentum(); //求解器参数中设置的冲量
Dtype local_rate = rate * net_params_lr[param_id]; //乘上系数,得到当前参数的学习率
// Compute the update to history, then copy it to the parameter diff.
switch (Caffe::mode()) {
case Caffe::CPU: {
//计算带冲量的梯度值,并将梯度保存在history_中,供下次迭代使用
caffe_cpu_axpby(net_params[param_id]->count(), local_rate,
net_params[param_id]->cpu_diff(), momentum,
history_[param_id]->mutable_cpu_data()); //history_data = local_rate * param_diff + momentum * history_data
caffe_copy(net_params[param_id]->count(),
history_[param_id]->cpu_data(),
net_params[param_id]->mutable_cpu_diff()); //param_diff = history_data
break;
}
case Caffe::GPU: {
#ifndef CPU_ONLY
//与cpu操作类似,该函数先是 history_data = local_rate * param_diff + momentum * history_data,
//再是 param_diff = history_data
sgd_update_gpu(net_params[param_id]->count(),
net_params[param_id]->mutable_gpu_diff(),
history_[param_id]->mutable_gpu_data(),
momentum, local_rate);
#else
NO_GPU;
#endif
break;
}
default:
LOG(FATAL) << "Unknown caffe mode: " << Caffe::mode();
}
}
//model_filename为网络的快照的文件名,将求解器的状态保存在快照文件中
template <typename Dtype>
void SGDSolver<Dtype>::SnapshotSolverState(const string& model_filename) {
switch (this->param_.snapshot_format()) { //快照的格式,二进制proto类型还是hdf5类型
case caffe::SolverParameter_SnapshotFormat_BINARYPROTO:
SnapshotSolverStateToBinaryProto(model_filename); //将求解器的状态存为二进制proto类型文件
break;
case caffe::SolverParameter_SnapshotFormat_HDF5:
SnapshotSolverStateToHDF5(model_filename); //将求解器的状态存为hdf5类型文件
break;
default:
LOG(FATAL) << "Unsupported snapshot format.";
}
}
//将SGDSolver的状态存入SolverState消息中,并存为文件
template <typename Dtype>
void SGDSolver<Dtype>::SnapshotSolverStateToBinaryProto(const string& model_filename) {
SolverState state;
state.set_iter(this->iter_); //将当前的迭代次数存入SolverState消息中
state.set_learned_net(model_filename); //将网络的快照文件名存入
state.set_current_step(this->current_step_); //存入迭代的阶段
state.clear_history(); //清空历史数据,SolverState消息中的各个参数的历史数据均为BlobProto类型的消息
for (int i = 0; i < history_.size(); ++i) {
// Add history
BlobProto* history_blob = state.add_history(); //增加参数的历史梯度信息
history_[i]->ToProto(history_blob); //并将求解器中blob类型history_的数据写入其中
}
string snapshot_filename = Solver<Dtype>::SnapshotFilename(".solverstate"); //生成".solverstate"扩展名的快照状态文件名
LOG(INFO) << "Snapshotting solver state to binary proto file " << snapshot_filename; //打印
WriteProtoToBinaryFile(state, snapshot_filename.c_str()); //将SolverState消息写入二进制的proto类型文件中
}
//将SGDSolver的iter_/model_filename/current_step_/history_写入到hdf5文件中
template <typename Dtype>
void SGDSolver<Dtype>::SnapshotSolverStateToHDF5(const string& model_filename) {
// This code is taken from https://github.com/sh1r0/caffe-android-lib
#ifdef USE_HDF5
string snapshot_filename = Solver<Dtype>::SnapshotFilename(".solverstate.h5"); //先生成文件名
LOG(INFO) << "Snapshotting solver state to HDF5 file " << snapshot_filename;
hid_t file_hid = H5Fcreate(snapshot_filename.c_str(), H5F_ACC_TRUNC, H5P_DEFAULT, H5P_DEFAULT); //创建hdf5文件
CHECK_GE(file_hid, 0) << "Couldn't open " << snapshot_filename << " to save solver state."; //检查是否创建成功
hdf5_save_int(file_hid, "iter", this->iter_); //在file_hid中创建名为"iter"的整形数据集,并将iter_值写入其中
hdf5_save_string(file_hid, "learned_net", model_filename); //创建"learned_net", 并将model_filename写入其中
hdf5_save_int(file_hid, "current_step", this->current_step_); //创建"current_step", 并写入
hid_t history_hid = H5Gcreate2(file_hid, "history", H5P_DEFAULT, H5P_DEFAULT, H5P_DEFAULT); //创建"history"组
CHECK_GE(history_hid, 0) << "Error saving solver state to " << snapshot_filename << ".";
for (int i = 0; i < history_.size(); ++i) {
ostringstream oss;
oss << i;
hdf5_save_nd_dataset<Dtype>(history_hid, oss.str(), *history_[i]); //创建Dtype类型的数据集,并将blob中的数据写入其中
}
H5Gclose(history_hid);
H5Fclose(file_hid);
// This code is taken from https://github.com/sh1r0/caffe-android-lib
#else
LOG(FATAL) << "SnapshotSolverStateToHDF5 requires hdf5;"
<< " compile with USE_HDF5.";
#endif // USE_HDF5
}
//从二进制proto文件state_file中读取求解器的状态,并存入当前求解器中.如果求解器状态中还设置了模型参数文件,则还会加载模型参数
template <typename Dtype>
void SGDSolver<Dtype>::RestoreSolverStateFromBinaryProto(
const string& state_file) {
SolverState state;
ReadProtoFromBinaryFile(state_file, &state); //从state_file文件中读取消息到state中
this->iter_ = state.iter(); //使用state中的值设置当前的求解器
if (state.has_learned_net()) { //如果设置了模型参数文件的路径
NetParameter net_param;
ReadNetParamsFromBinaryFileOrDie(state.learned_net().c_str(), &net_param); //从文件中读取网络参数
this->net_->CopyTrainedLayersFrom(net_param); //数据拷贝至当前网络中
}
this->current_step_ = state.current_step(); //设置
CHECK_EQ(state.history_size(), history_.size())
<< "Incorrect length of history blobs."; //检查state中历史数据的个数与当前求解器中历史数据的个数是否匹配
LOG(INFO) << "SGDSolver: restoring history";
for (int i = 0; i < history_.size(); ++i) {
history_[i]->FromProto(state.history(i)); //从state中拷贝历史梯度数据至当前求解器中
}
}
//从hdf5文件state_file中读取求解器的状态,并存入当前求解器中.如果求解器状态中还设置了模型参数文件,则还会加载模型参数
template <typename Dtype>
void SGDSolver<Dtype>::RestoreSolverStateFromHDF5(const string& state_file) {
#ifdef USE_HDF5
hid_t file_hid = H5Fopen(state_file.c_str(), H5F_ACC_RDONLY, H5P_DEFAULT); //打开文件
CHECK_GE(file_hid, 0) << "Couldn't open solver state file " << state_file; //检查操作是否成功
this->iter_ = hdf5_load_int(file_hid, "iter"); //从file_hid中读取"iter"数据集中的整数,存入iter_中
if (H5LTfind_dataset(file_hid, "learned_net")) { //判断file_hid中是否存在名为"learned_net"的数据集
//读取该数据集中的字符串,"learned_net"中存放的是网络模型参数文件的文件名(**.caffemodel.h5)
string learned_net = hdf5_load_string(file_hid, "learned_net");
this->net_->CopyTrainedLayersFrom(learned_net); //读取模型参数文件,加载网络参数
}
this->current_step_ = hdf5_load_int(file_hid, "current_step"); //读取"current_step"中的值
hid_t history_hid = H5Gopen2(file_hid, "history", H5P_DEFAULT); //打开"history"数据集
CHECK_GE(history_hid, 0) << "Error reading history from " << state_file;
int state_history_size = hdf5_get_num_links(history_hid); //获取其中links(元素)的个数
CHECK_EQ(state_history_size, history_.size())
<< "Incorrect length of history blobs."; //同样检查是否与当前求解器中的history_匹配
for (int i = 0; i < history_.size(); ++i) {
ostringstream oss;
oss << i;
hdf5_load_nd_dataset<Dtype>(history_hid, oss.str().c_str(), 0,
kMaxBlobAxes, history_[i].get()); //从history_hid中读取数据,存入history_[i]中
}
H5Gclose(history_hid);
H5Fclose(file_hid);
#else
LOG(FATAL) << "RestoreSolverStateFromHDF5 requires hdf5;"
<< " compile with USE_HDF5.";
#endif // USE_HDF5
}# 参照代码中的GetLearningRate()函数,用Python简单实现了下不同学习率策略的效果,方便有个直观的了解
import numpy as np
from math import exp
import matplotlib.pyplot as plt
base_lr = 0.01
max_iter = np.arange(3000)
def fixed(iter):
return base_lr
def step(iter):
step_size = 500
gamma = 0.7
current_step = int(iter / step_size)
return base_lr * pow(gamma, current_step)
def exp_policy(iter):
gamma = 0.99
return base_lr * pow(gamma, iter)
def inv(iter):
gamma = 0.001
power = 0.75
return base_lr * pow(1 + gamma * iter, -power)
class multistep(object):
gamma = 0.7
stepvalue = np.array([200, 800, 1500, 2300])
multistep_current_step = 0
def rate(self, iter):
if (self.multistep_current_step < self.stepvalue.shape[0] and
iter >= self.stepvalue[self.multistep_current_step]):
self.multistep_current_step += 1
return base_lr * pow(self.gamma, self.multistep_current_step)
def poly(iter):
power = 2
return base_lr * pow(1 - iter / max_iter.shape[0], power)
def sigmoid(iter):
gamma = -0.01
step_size = 1500
return base_lr * (1 / (1 + exp(-gamma * (iter - step_size))))
rate_fixed = np.array([fixed(iter) for iter in max_iter])
rate_step = np.array([step(iter) for iter in max_iter])
rate_exp_policy = np.array([exp_policy(iter) for iter in max_iter])
rate_inv = np.array([inv(iter) for iter in max_iter])
mltstp = multistep()
rate_multistep = np.array([mltstp.rate(iter) for iter in max_iter])
rate_poly = np.array([poly(iter) for iter in max_iter])
rate_sigmoid = np.array([sigmoid(iter) for iter in max_iter])
plt.figure(1)
ax1 = plt.subplot(3, 3, 1)
ax2 = plt.subplot(3, 3, 2)
ax3 = plt.subplot(3, 3, 3)
ax4 = plt.subplot(3, 3, 4)
ax5 = plt.subplot(3, 3, 5)
ax6 = plt.subplot(3, 3, 6)
ax7 = plt.subplot(3, 3, 7)
plt.sca(ax1)
ax1.set_title('fixed')
plt.plot(max_iter, rate_fixed)
plt.sca(ax2)
ax2.set_title('step')
plt.plot(max_iter, rate_step)
plt.sca(ax3)
ax3.set_title('exp')
plt.plot(max_iter, rate_exp_policy)
plt.sca(ax4)
ax4.set_title('inv')
plt.plot(max_iter, rate_inv)
plt.sca(ax5)
ax5.set_title('multistep')
plt.plot(max_iter, rate_multistep)
plt.sca(ax6)
ax6.set_title('poly')
plt.plot(max_iter, rate_poly)
plt.sca(ax7)
ax7.set_title('sigmoid')
plt.plot(max_iter, rate_sigmoid)
plt.show()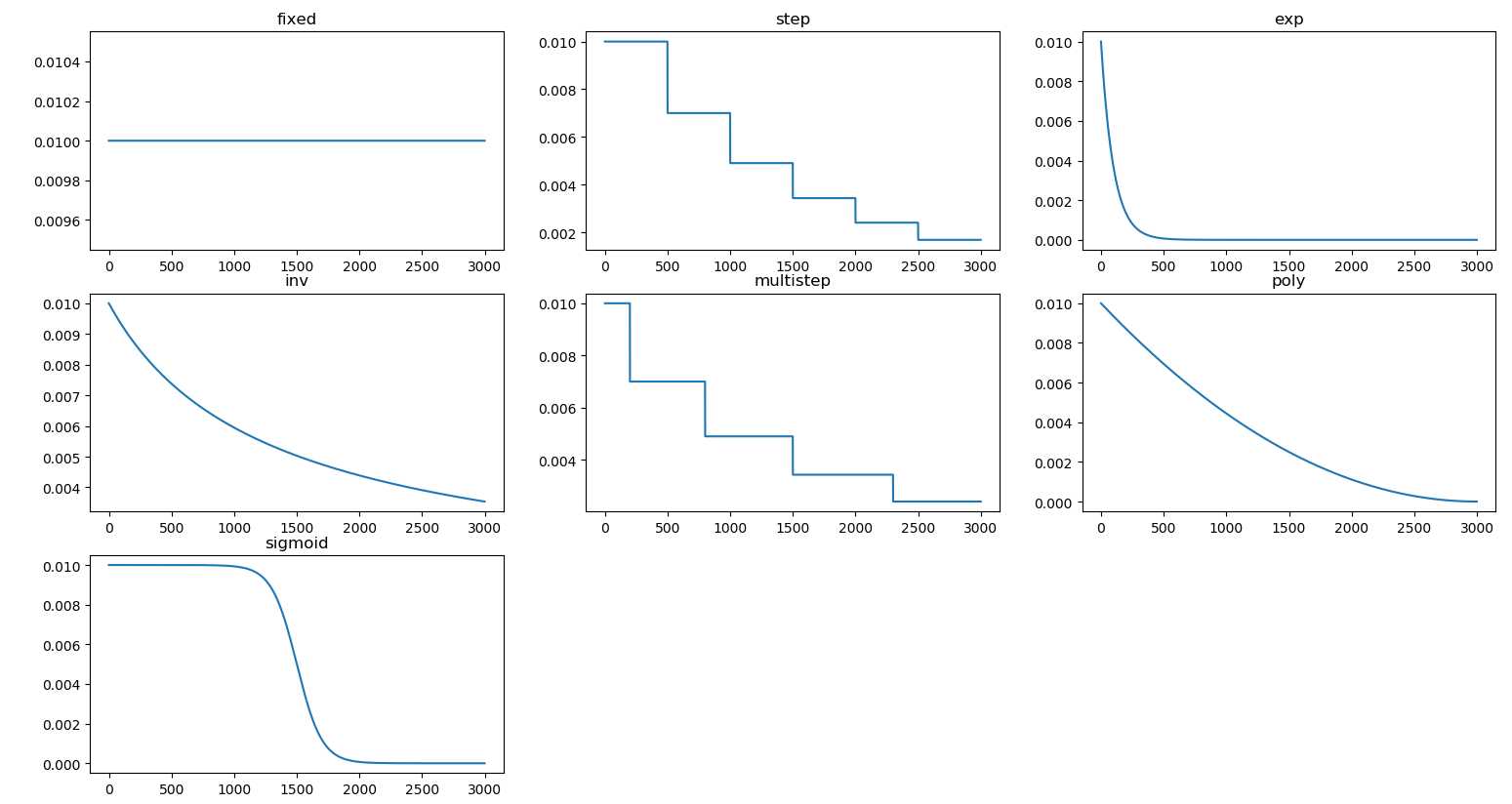
Caffe的源码笔者是第一次阅读,一边阅读一边记录,对代码的理解和分析可能会存在错误或遗漏,希望各位读者批评指正,谢谢支持!
标签:date() 分析 leo 形状 similar github 不用 counter binary
原文地址:https://www.cnblogs.com/Relu110/p/12064759.html