标签:数据 head 邻接表 kruskal算法 连通 序列 多重 选择 lis
数据结构第七到十章
期末复习总结
写在前面:期末数据结构继续给爷冲!
第七章:图无
无向完全图:有n个顶点的话,含n(n-1)/2条边,
有向完全图:有n个顶点则含n(n-1)条弧
简单路径:若路径中的中顶点不重复出现,则该路径称为简单路径。从顶点v1到顶点v5的两条路径都为简单路径。
简单回路:除第一个顶点和最后一个顶点之外,其他顶点不重复出现的回路称为简单回路,或者简单环。
连通图:若对于图中 任意两个顶点都是连 通的,则称该图是连通图。
连通分量:指无向 图中极大连通子图。
生成树:所谓连通图G的生成树,是G的包含其全部n个顶点的一个极小连通子图。它必定包含且包含G的n-1条边。
图的存储方式:
1.图的数组(邻接矩阵)存储
2.图的邻接表存储
3.有向图的十字链表存储
4.无向图的临界多重表存储
1.邻接矩阵表示法:
无权图的矩阵里,0表示无边(弧),1表示有边(弧);
有权图里,有边(弧)写权值,无边(弧)写无穷大
typedef struct ArcCell{
VRType adj;
InfoType *info; //该弧相关信息的指针
}ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
图的定义:
tpyedef struct{
VertexType vexs[MAX_VERTEX_NUM]; //顶点向量
AdjMatrix arcs; //邻接矩阵
int vexnum,arcnum; //图的当前顶点数和弧数
GraphKind kind; //图的种类标志
}MGraph;
构造方法:
1、输入顶点、边数目及边信息
scanf(&G.vexnum,&G.arcnum,IncInfo); //IncInfo为0则各弧不含其它信息
2、构造顶点向量
for(i=0;i<G.vexnum;++i) scanf(G.vexs[i]);
3、初始化邻接矩阵
for(i=0;i<G.vexnum;++i) for(j=0;j<G.vexnum;++j) { G.arcs[i][j].adj=INFINITY; //网,INFINITY为无穷大 G.arcs[i][j].info=NULL; }
4、构造邻接矩阵
int LocateVex(MGraph G, VertexType v) {
for (i=0; i<G.vexnum;++i)
if (G.vexs[i]==v)
return i;
}

2.邻接表表示法:
顶点的结点结构(头结点)

typedef struct VNode {
VertexType data; // 顶点信息
ArcNode *firstarc; // 指向第一条依附该顶点的弧
} VNode, AdjList[MAX_VERTEX_NUM];
弧的结点结构(表结点)
![]()
typedef struct ArcNode {
int adjvex; // 该弧所指向的顶点的位置
struct ArcNode *nextarc; // 指向下一条弧的指针
InfoType *info; // 该弧相关信息的指针
} ArcNode;
图的结构定义:
typedef struct {
AdjList vertices;
int vexnum, arcnum; int kind; // 图的种类标志
} ALGraph;
无向带权图建立邻接表的方法:
邻接表的表头数组初始化
for (i=0;i<G.vexnum;++i) {
scanf(&G.vertices[i].data);
G.vertices[i].firstarc=NULL;
}
输入图中每一条边的顶点对及其边上的权,新建一个表结点:
for (k=0;k<G. edgenum;++k) {
scanf(&V1, &V2);
i=LocateVex(G,V1); j=LocateVex(G,V2);
P=(ArcNode *)malloc(sizeof(ArcNode));
P.adjvex=j;
P.nextarc=G.vertices[i].firstarc;
G.vertices[i].firstarc=P;//注意是要从表头插入,每次都是找到表头结点 将新的节点插入
P=(ArcNode *)malloc(sizeof(ArcNode));
P.adjvex=i;
P.nextarc=G.vertices[j].firstarc;
G.vertices[j].firstarc=P;//由于是无向图,则应该是i和j互换然后构造从j到i的弧
if (IncInfo) Input (*P->info);
}
3.十字链表表示法:
弧结点的结构:

尾域(tailvex)和头域(headvex)分别指示弧尾和弧头这两个顶点在图中的位置;
链域hlink指向弧头相同的下一条弧,而链域tlink指向弧尾相同的下一条弧,info域指向该弧的相关信息。
顶点结点(头结点):
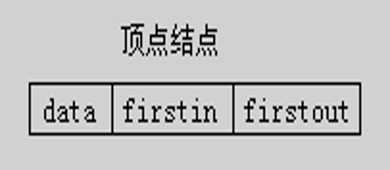
由三个域组成:
data域存储和顶点相关的信息,如顶点的名称等;
firstin和firstout为两个链域,分别指向以该顶点为弧头或弧尾的第一个弧结点。

4.无向图的邻接多重表:
表头结点(顶点):

data 存储和该顶点有关的信息,
firstedge指示第一条依附于该顶点的边。
typedef struct VexBox{
VertexType data;
Ebox *firstedge; //指向第一条依附该顶点的边
}VexBox;
边结点:

mark为标志域,可用于标记该条边是否被搜索过;
ivex和jvex为该边依附的两个顶点在图中的位置;
ilink指向下一条依附于该顶点ivex的边;
jlink指向下一条依附于顶点jvex的边;
info为指向和边相关的各种信息的指针域。
#define MAX_VERTEX_NUM 20
typedef emnu{unvisited, visited} VisitIf;
typedef struct EBox{
VisitIf mark; //访问标记
int ivex, jvex; //该边依附的两个顶点的位置
struct Ebox *ilink, *jlink; //分别指向依附这两个顶点的下一条边
InfoType *info; //该边信息指针
}EBox;
图的表示:
typedef struct {
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum,edgenum; //无向图的当前顶点数和边数
}AMLGraph;
图的遍历:
分为深搜和广搜
深度优先搜索:
时间复杂度分析:
假设n为图的顶点数目,e为图的边数,
当以邻接矩阵作为图的存储结构时,查找一个顶点的邻接点所需时间为O(n),因此,整个算法的时间复杂度为 O(n^2)。
当以邻接表作存储结构时,找邻接点所需时间为O(e),因此深度优先搜索遍历图的时间复杂度为O(n+e)(初始化需要O(n))。
广度优先搜索:
广度优先搜索遍历图的过程是以v为起始点,由近至远,依次访问和v有路径相通且路径长度为1,2,…的顶点。
从图中的某个顶点V0出发,并在访问此顶点之后依次访问V0的所有未被访问过的邻接点,之后按这些顶点被访问的先后次序依次访问它们的邻接点,直至图中所有和V0有路径相通的顶点都被访问到。
时间复杂度分析:
广度优先搜索和深度优先搜索的时间复杂度相同,区别仅在于遍历结点的顺序不同
求无向图的连通分量:
方法:
1.从图中任选一个未被访问的顶点v,从顶点v开始进行深度或广度优先搜索,在本次搜索中被访问的所有顶点以及它们之间的边就构成了包含顶点v的连通分量;
2.然后在从图中选择一个未被访问的顶点,进行搜索,求得下一个连通分量;
3.依次类推,直到图中所有顶点都被访问。这种求无向图的连通分量的算法与图的遍历算法几乎完全相同。
求连通图的生成树:
遍历该连通图得到的所有结点和边构成一个含n个顶点(n-1)条边的生成树。
由深度优先搜索得到的生成树称为深度优先生成 树,简称DFS生成树;
由广度优先搜索得到的生成树称为广度优先生成树,简称BFS生成树。
最小生成树:
两种算法:普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法
Prim算法:
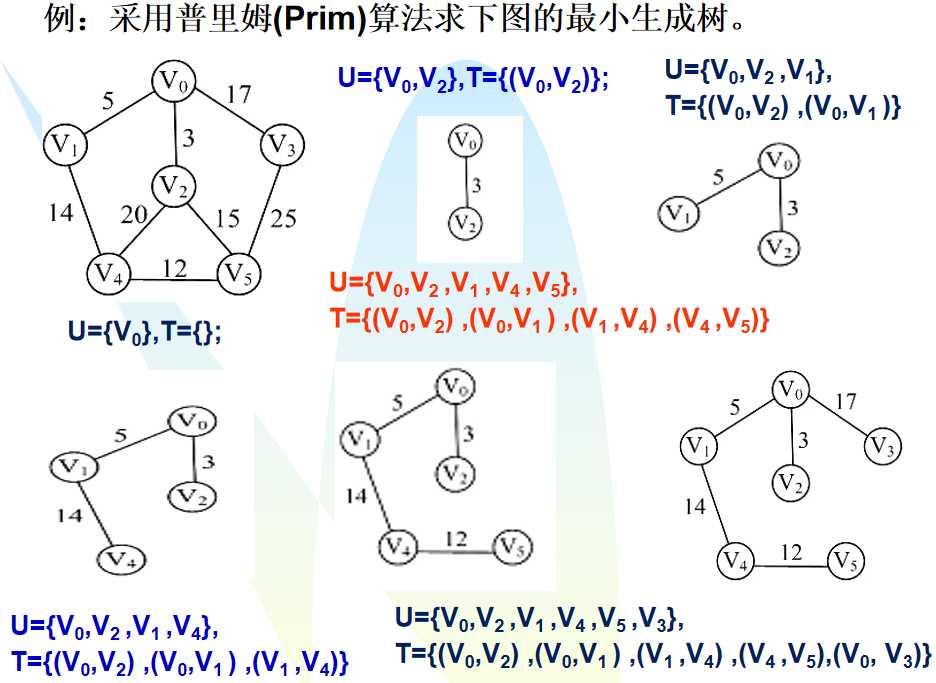
时间复杂度分析:
Prim算法时间复杂度为O(n2),与边的数目无关。
Kruskal算法:
有向无环图及其应用:
拓扑排序
AOV网:
用顶点表示活动,用弧表示活动优先关系的有向图,称为顶点表示活动的网(AOV)。
在AOV网中,如果从顶点i到顶点j有一条有向路径,则称i是j的前趋,j是i的后继。
若<i,j>是AOV网中的一条弧,则i 是j的直接前趋,j是i的直接后继。
在AOV网中,不应该出现有向环,因为存在环意味着某项活动应以自己为先决条件。
检查有AOV网中是否存在环的方法之一,是对有向图进行拓扑排序。 若网中的所有顶点都在它的拓扑有序序列中,则该AOV-网中必定不存在环。
求拓扑排序序列的方法:
1.从有向图中选取一个没有前驱 的顶点,并输出之;
2.从有向图中删去此顶点以及所 有以它为尾的弧;
3.重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
y图
yyyo:
标签:数据 head 邻接表 kruskal算法 连通 序列 多重 选择 lis
原文地址:https://www.cnblogs.com/xxikwonxjlxi/p/12066645.html